Irodov Solutions: Conductors And Dielectrics In An Electric Field- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 71. An electric field of strength E = 1.0 kV/cm produces polarization in water equivalent to the correct orientation of only one out of N molecules. Find N. The electric moment of a water molecule equals p = 0.62-10-29 C•m.
Solution. 71. The total polarization is 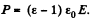 This must equals
This must equals 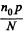 here n0 is the concemtation of water molecules. Thus
here n0 is the concemtation of water molecules. Thus
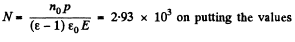
Q. 72. A non-polar molecule with polarizability β is located at a great distance l from a polar molecule with electric moment p. Find the magnitude of the interaction force between the molecules if the vector p is oriented along a straight line passing through both molecules.
Solution. 72. From the general formula
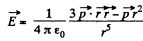
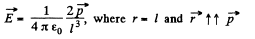
This will cause the induction of a dipole moment.
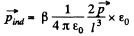
Thus the force,

Q. 73. A non-polar molecule is located at the axis of a thin uniformly charged ring of radius R. At what distance x from the ring's centre is the magnitude of the force F acting on the given molecule (a) equal to zero; (b) maximum?
Draw the approximate plot Fx (x).
Solution. 73. The electric field E at distance x from the centre of the ring is,
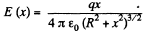
The induced dipole moment is 
The force on this molecule is
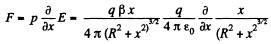
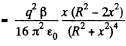
This vanishes for 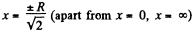
It is maximum when
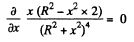
or, 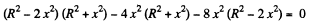
or, 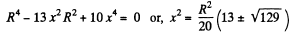
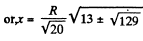 (on either side), Plot of Fx (x) is as shown in the answersheet.
(on either side), Plot of Fx (x) is as shown in the answersheet.
Q. 74. A point charge q is located at the centre of a ball made of uniform isotropic dielectric with permittivity ε. Find the polarization P as a function of the radius vector r relative to the centre of the system, as well as the charge q' inside a sphere whose radius is less than the radius of the ball.
Solution. 74. Inside the ball
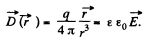
Also 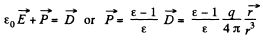
Also, 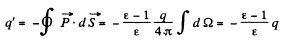
Q. 75. Demonstrate that at a dielectric-conductor interface the surface density of the dielectric's bound charge σ' = -σ (ε — 1)/ε, where a is the permittivity, a is the surface density of the charge on the conductor.
Solution. 75.
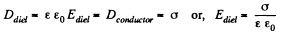
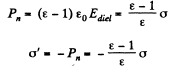
This is the surface density of bound charges.
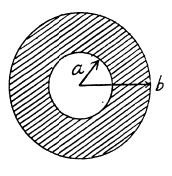
Q. 76. A conductor of arbitrary shape, carrying a charge q, is surrounded with uniform dielectric of permittivity 8 (Fig. 3.9). Find the total bound charges at the inner and outer surfaces of the dielectric.
Solution. 76. From the solution o f the previous problem q'in = charge on the interior surface o f the conductor
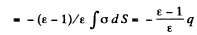
Since the dielectric as a whole is neutral there must be a total charge equal to
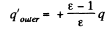 on the outer surface of the dielectric.
on the outer surface of the dielectric.
Q. 77. A uniform isotropic dielectric is shaped as a spherical layer with radii a and b. Draw the approximate plots of the electric field strength E and the potential φ vs the distance r from the centre of the layer if the dielectric has a certain positive extraneous charge distributed uniformly:
(a) over the internal surface of the layer;
(b) over the volume of the layer.
Solution. 77. (a) Positive extraneous charge is distributed uniformly over the internal surface layer. Let σ0 be the surface density of the charge.
Clearly, E = 0, for r < a
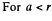
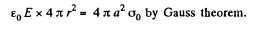
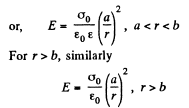
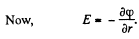
So by integration from infinity where φ(∞) = 0,
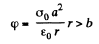
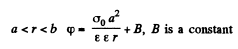
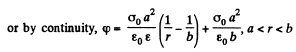
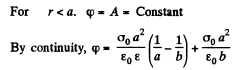
(b) Positive extraneous charge is distributed uniformly over the internal volume of the dielectric
Let p0 = Volume density of the charge in the dielectric, for a < r < b.
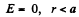

or, 
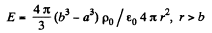
or, 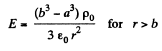
By integration,
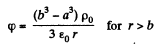
or, 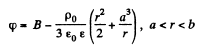
By continuity 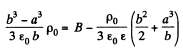
or, 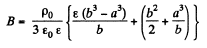
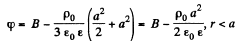
On the basis of obtained expressions E (r) and (φ) (r) can be plotted as shown in the answer-sheet.
Q. 78. Near the point A (Fig. 3.10) lying on the boundary between glass and vacuum the electric field strength in vacuum is equal to E0 = 10.0 V/m, the angle between the vector E0 and the normal n of the boundary line being equal to α0 = 30°. Find the field strength E in glass near the point A, the angle α between the vector E and n, as well as the surface density of the bound charges at the point A.

Solution. 78. Let the field in the dielectric be 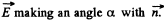 Then we have the boundary conditions,
Then we have the boundary conditions,
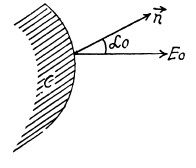
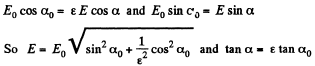
In the dielectric the normal component of the induction vector is
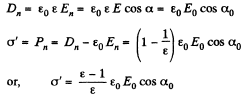
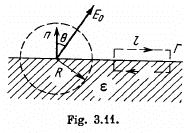
Q. 79. Near the plane surface of a uniform isotropic dielectric with permittivity ε the electric field strength in vacuum is equal to E0, the vector E0 forming an angle θ with the normal of the dielectric's surface (Fig. 3.11). Assuming the field to be uniform both inside and outside the dielectric, find:
(a) the flux of the vector E through a sphere of radius R with centre located at the surface of the dielectric;
(b) the circulation of the vector D around the closed path  of length I (see Fig. 3.11) whose plane is perpendicular to the surface of the dielectric and parallel to the vector E0.
of length I (see Fig. 3.11) whose plane is perpendicular to the surface of the dielectric and parallel to the vector E0.
Solution. 79. From the previous problem, 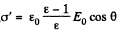

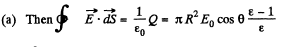
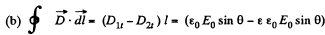
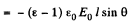
Q. 80. An infinite plane of uniform dielectric with permittivity ε is uniformly charged with extraneous charge of space density p. The thickness of the plate is equal to 2d. Find:
(a) the magnitude of the electric field strength and the potential as functions of distance l from the middle point of the plane (where the potential is assumed to be equal to zero); having chosen the x coordinate axis perpendicular to the plate, draw the approximate plots of the projection Ex(x) of the vector E and the potential φ(x);
(b) the surface and space densities of the bound charge.
Solution. 80. 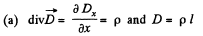
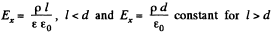
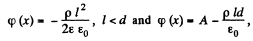
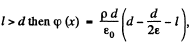
by continuity.
On the basis o f obtained expressions Ex (x) and qp (x) can be plotted as shown in the figure of answersheet.
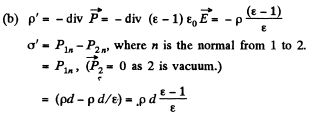
Q. 81. Extraneous charges are uniformly distributed with space density p > 0 over a ball of radius R made of uniform isotropic dielectric with permittivity a. Find:
(a) the magnitude of the electric field strength as a function of distance r from the centre of the ball; draw the approximate plots E (r) and φ (r);
(b) the space and surface densities of the bound charges.
Solution. 81.
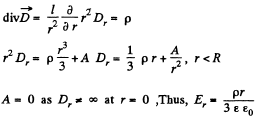
For 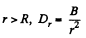
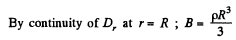
so, 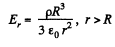
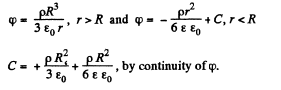
See answer sheet for graphs of E (r) and φ (r)
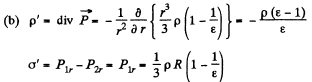
Q. 82. A round dielectric disc of radius R and thickness d is statically polarized so that it gains the uniform polarization P, with the vector P lying in the plane of the disc. Find the strength E of the electric field at the centre of the disc if d ≪ R.
Solution. 82. Because there is a discontinuity in polarization at the boundary of the dielectric disc, a bound surface charge appears, which is the source of the electric Held inside and outside the disc.
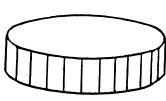
We have for the electric field at the origin.
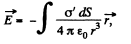
 radius vector to the origin from the element dS.
radius vector to the origin from the element dS.

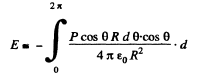
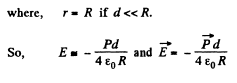
Q. 83. Under certain conditions the polarization of an infinite uncharged dielectric plate takes the form P = P0 (1 — x2/d2), where P0 is a vector perpendicular to the plate, x is the distance from the middle of the plate, d is its half-thickness. Find the strength E of the electric field inside the plate and the potential difference between its surfaces.
Solution. 83. Since there are no free extraneous charges anywhere
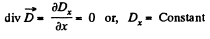
But 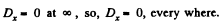
Thus, 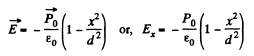
So, 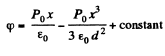
Hence,
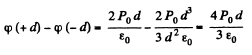
Q. 84. Initially the space between the plates of the capacitor is filled with air, and the field strength in the gap is equal to E0. Then half the gap is filled with uniform isotropic dielectric with permittivity a as shown in Fig. 3.12. Find the moduli of the vectors E and D in both parts of the gap (1 and 2) if the introduction of the dielectric
(a) does not change the voltage across the plates;
(b) leaves the charges at the plates constant.
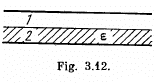
Solution. 84.
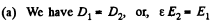
Also, 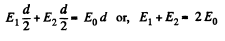
Hence, 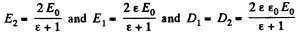
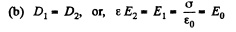
Thus, 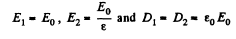
Q. 85. Solve the foregoing problem for the case when half the gap is filled with the dielectric in the way shown in Fig. 3.13.
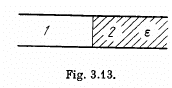
Solution. 85. (a) Constant voltage acros the plates;
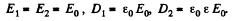
(b) Constant charge across the plates;
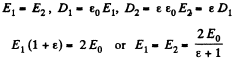
FAQs on Irodov Solutions: Conductors And Dielectrics In An Electric Field- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the difference between conductors and dielectrics in an electric field? |  |
| 2. How do conductors and dielectrics behave in an electric field? |  |
| 3. Can a material act as both a conductor and a dielectric? |  |
| 4. What is the role of conductors and dielectrics in electrical circuits? |  |
| 5. How does the presence of conductors and dielectrics affect the electric field strength? |  |

|
Explore Courses for JEE exam
|

|

















