Irodov Solutions: Dispersion and Absorption of Light- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.213. A plane monochromatic light wave of intensity l0 falls normally on a plane-parallel plate both of whose surfaces have a reflection coefficient p. Taking into account multiple reflections, find the intensity of the transmitted light if
(a) the plate is perfectly transparent, i.e. the absorption is absent;
(b) the coefficient of linear absorption is equal to x, and the plate thickness is d.
Ans. (a) The multiple reflections are shown below. Transmission gives a factor (1 - p) while reflections give factors of p. Thus the transmitted intensity assuming incoheren light is
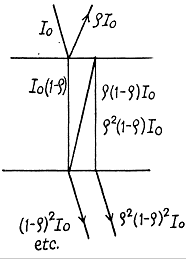
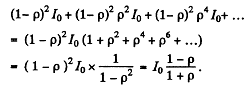
(b) When there is absorption, we pick up a factor 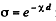 in each traversal of the plate. Thus we get
in each traversal of the plate. Thus we get
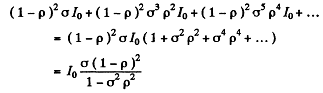
Q.214. Two plates, one of thickness d1 =3 .8 mm and the other of thickness d2 = 9.0 mm, are manufactured from a certain substance. When placed alternately in the way of monochromatic light, the first transmits ζ1 = 0.84 fraction of luminous flux and the second, ζ2 = 0.70. Find the coefficient of linear absorption of that substance. Light falls at right angles to the plates. The secondary reflections are to be neglected.
Ans. We have
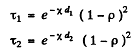
where p is the reflectivity; see previous problem, multiple reflection have been ignored.
Thus 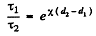
or 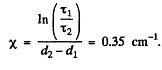
Q.215. A beam of monochromatic light passes through a pile of N = 5 identical plane-parallel glass plates each of thickness l = = 0.50 cm. The coefficient of reflection at each surface of the plates is p = 0.050. The ratio of the intensity of light transmitted through the pile of plates to the intensity of incident light is ζ = 0.55. Neglecting the secondary reflections of light, find the absorption coefficient of the given glass.
Ans. On each surface we pick up a factor (1 - p) from reflection and a factor 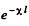 due to absorption in each plate.
due to absorption in each plate.

Q.216. A beam of monochromatic light falls normally on the surface of a plane-parallel plate of thickness l. The absorption coefficient of the substance the plate is made of varies linearly along the normal to its surface from x1 to x2. The coefficient of reflection at each surface of the plate is equal to p. Neglecting the secondary reflections, find the transmission coefficient of such a plate.
Ans. Apart from the factor (1 - p) on each end face of the plate, we shall get a factor due to absorptions. This factor can be calculated by assuming the plate to consist of a large number of very thin slab within each of which the absorption coefficient can be assumed to be constant Thus we shall get a product like
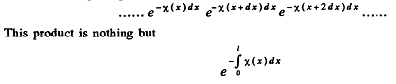
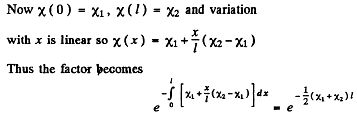
Q.217. A beam of light of intensity l0 falls normally on a transparent plane-parallel plate of thickness l. The beam contains all the wavelengths in the interval from X1 t o X2 of equal spectral intensity. Find the intensity of the transmitted beam if in this wavelength interval the absorption coefficient is a linear function of X, with extreme values x1 and x2. The coefficient of reflection at each surface is equal to p. The secondary reflections are to be neglected.
Ans. The spectral density of the incident beam (i.e. intensity of the components whose wave length lies in the interval

The absorption factor for this component is
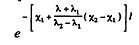
and the transmission factor due to reflection at the surface is ( 1 - p) 2. Thus the intensity of the transmitted beam is
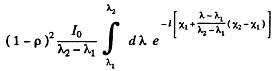
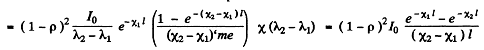
Q.218. A light filter is a plate of thickness d whose absorption coefficient depends on wavelength λ as
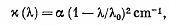
where α and λ0 are constants. Find the passband Δλ of this light filter, that is the band at whose edges the attenuation of light is times that at the wavelength λ0. The coefficient of reflection from the surfaces of the light filter is assumed to be the same at all wavelengths.
Ans. At the wavelength λ0 the absorption coefficient vanishes and loss in transmission is entirely due to reflection. This factor is the same at all wavelengths and therefore cancels out in calculating the pass band and we need not worry about it Now
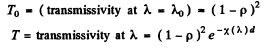

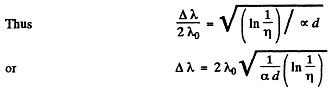
Q.219. A point source of monochromatic light emitting a luminous flux 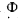 is positioned at the centre of a spherical layer of substance. The inside radius of the layer is a, the outside one is b. The coefficient of linear absorption of the substance is equal to x, the reflection coefficient of the surfaces is equal to p. Neglecting the secondary reflections, find the intensity of light that passes through that layer.
is positioned at the centre of a spherical layer of substance. The inside radius of the layer is a, the outside one is b. The coefficient of linear absorption of the substance is equal to x, the reflection coefficient of the surfaces is equal to p. Neglecting the secondary reflections, find the intensity of light that passes through that layer.
Ans. We have to derive the law of decrease of intensity in ah absorbing medium taking in to account the natural geometrical fall-off (inverse sequare law) as well as absorption.
Consider a thin spherical shell of thickness dx and internal radius x. Let
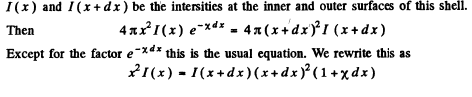
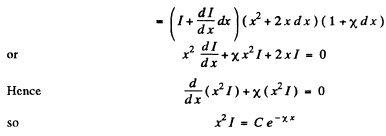
where C is a constant of integration.
In our case we apply this equation for 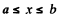
For x ≤ a the usual inverse square law gives
Hence 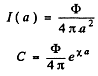
and 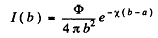
This does not take into account reflections. When we do that we get
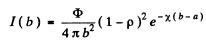
Q.220. How many times will the intensity of a narrow X-ray beam of wavelength 20 pm decrease after passing through a lead plate of thickness d = 1.0 mm if the mass absorption coefficient for the given radiation wavelength is equal to μ/p = 3.6 cm2/g?
Ans. The transmission factor is 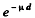 and so the intensity will decrease
and so the intensity will decrease

Q.221. A. narrow beam of X-ray radiation of wavelength 62 pm penetrates an aluminium screen 2.6 cm thick. How thick must a lead screen be to attenuate the beam just as much? The mass absorption coefficients of aluminium and lead for this radiation are equal to 3.48 and 72.0 cm2/g respectively.
Ans.
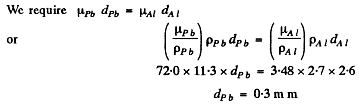
Q.222. Find the thickness of aluminium layer which reduces by half the intensity of a narrow monochromatic X-ray beam if the corresponding mass absorption coefficient is μ/p = 0.32 cm2/g.
Ans.
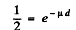
or 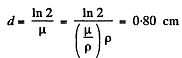
Q.223. How many 50%-absorption layers are there in the plate reducing the intensity of a narrow X-ray beam η = 50 times?
Ans. We require N plates where
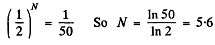

|
Explore Courses for JEE exam
|

|

















