Irodov Solutions: Dynamics of A Solid Body- 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 266. Determine the kinetic energy of a tractor crawler belt of mass m if the tractor moves with velocity v (Fig. 1.69).
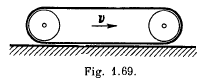
Solution. 266. Since the lower part of the belt is in contact with the rigid floor, velocity of this part becomes zero. The crawler moves with velocity v, hence the velocity of upper part of the belt becomes 2v by the rolling condition and kinetic energy of upper part 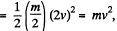 which is also the sought kinetic energy, assuming that the length of the belt is much larger than the radius of the wheels.
which is also the sought kinetic energy, assuming that the length of the belt is much larger than the radius of the wheels.
Q. 267. A uniform sphere of mass In and radius r rolls without sliding over a horizontal plane, rotating about a horizontal axle OA (Fig. 1.70). In the process, the centre of the sphere moves with velocity v along a circle of radius R. Find the kinetic energy of the sphere.
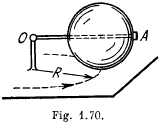
Solution. 267. The sphere has two types of motion, one is the rotation about its own axis and the other is motion in a circle of radius R. Hence the sought kinetic energy
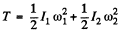 (1)
(1)
where is the moment of inertia about its own axis, and I2 is the moment of inertia about the vertical axis, passing through O,
But, 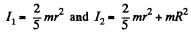 (using parallel axis theorem,) (2)
(using parallel axis theorem,) (2)
In addition to
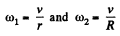 (3)
(3)
Using (2) and (3) in (1), we get 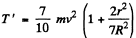
Q. 268. Demonstrate that in the reference frame rotating with a constant angular velocity ω about a stationary axis a body of mass m experiences the resultant
(a) centrifugal force of inertia Fcf = mω2Rc, where Rc is the radius vector of the body's centre of inertia relative to the rotation axis;
(b) Coriolis force Fcor = 2m [v'cω], where is the velocity of the body's centre of inertia in the rotating reference frame
Solution. 268. For a point mass of mass dm, looked at from C rotating frame, the equation is
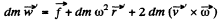
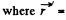 radius vector in the rotating frame with respect to rotation axis and
radius vector in the rotating frame with respect to rotation axis and 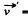 velocity in the same frame. The total centrifugal force is clearly
velocity in the same frame. The total centrifugal force is clearly
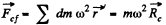
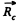 is the radius vector of the C.M. of the body with respect to rotation axis, also
is the radius vector of the C.M. of the body with respect to rotation axis, also
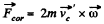
where we have used the definitions
Q. 269. A midpoint of a thin uniform rod AB of mass m and length l is rigidly fixed to a rotation axle OO' as shown in Fig. 1.71. The rod is set into rotation with a constant angular velocity ω. Find the resultant moment of the centrifugal forces of inertia relative to the point C in the reference frame fixed to the axle OO' and to the rod.
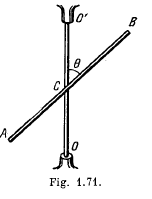
Solution. 269. Consider a small element of length dx at a distance x from the point C, which is rotating in a circle of radius r = x sin θ
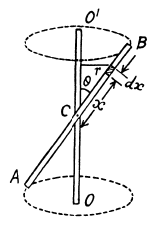
Now, mass of the element 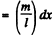
So, centrifugal force acting on this element  and moment of this force about C,
and moment of this force about C,
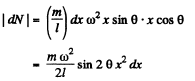
and hence, total moment
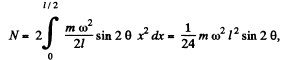
Q. 270. A conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω (the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
Solution. 270. Let us consider the system in a frame rotating with the rod. In this frame, the rod is at rest and experiences not only the gravitational force  the reaction force
the reaction force 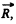 but also the centrifugal force
but also the centrifugal force 
In the considered frame, from the condition of equilibrium i.e. 
or, 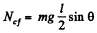 (1)
(1)
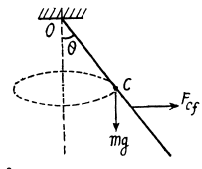
where Ncf is the moment of centrifugal force about O. To calculate Ncf, let us consider an element of length dx, situated at a distance x from the point O. This element is subjected to a horizontal pseudo force 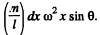 The moment of this pseudo force about the axis of rotation through the point O is
The moment of this pseudo force about the axis of rotation through the point O is
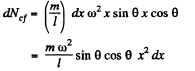
So 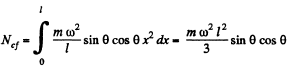 (2)
(2)
It follows from Eqs. (1) and (2) that,
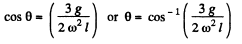 (3)
(3)
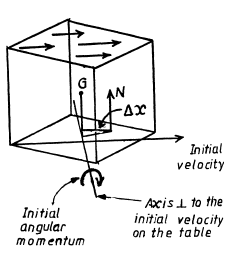
Q. 271. A uniform cube with edge a rests on a horizontal plane whose friction coefficient equals k. The cube is set in motion with an initial velocity, travels some distance over the plane and comes to a stand- still. Explain the disappearance of the angular momentum of the cube relative to the axis lying in the plane at right angles to the cube's motion direction. Find the distance between the resultants of gravitational forces and the reaction forces exerted by the supporting plane.
Solution. 271. When the cube is given an initial velocity on the table in some direction (as shown) it acquires an angular momentum about an axis on the table perpendicular to the initial velocity and (say) just below the C.G.. This angular momentum will disappear when the cube stops and this can only by due to a torque. Frictional forces cannot do this by themselves because they act in the plain containing the axis. But if the force of normal reaction act eccentrically (as shown), their torque can bring about the vanishing of the angular momentum. We can calculate the distance Ax between the point of application of the normal reaction and the C.G. of the cube as follows. Take the moment about C.G. of all the forces. This must vanish because the cube does not turn or tumble on the table. Then if the force of friction is fr
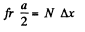
But N = mg and fr = kmg, so
Δx = ka/2
Q. 272. A smooth uniform rod AB of mass M and length l rotates freely with an angular velocity ω0, in a horizontal plane about a stationary vertical axis passing through its end A. A small sleeve of mass m starts sliding along the rod from the point A. Find the velocity v' of the sleeve relative to the rod at the moment it reaches its other end B.
Solution. 272. In the process of motion of the given system the kinetic energy and the angular momentum relative to rotation axis do not vary. Hence, it follows that
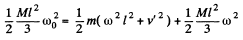
(ω is the final angular velocity of the rod)
and 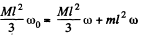
From these equations we obtain
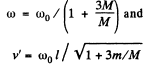
Q. 273. A uniform rod of mass m = 5.0 kg and length l = 90 cm rests on a smooth horizontal surface. One of the ends of the rod is struck with the impulse J = 3.0 N•s in a horizontal direction perpendicular to the rod. As a result, the rod obtains the momentum p = 3.0 N.s. Find the force with which one half of the rod will act on the other in the process of motion.
Solution. 273. Due to hitting of the ball, the angular impulse received by the rod about the C.M. is equal to 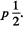 If ω is the angular velocity acquired by the rod, we hav
If ω is the angular velocity acquired by the rod, we hav
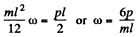 (1)
(1)
In the frame of C.M., the rod is rotating about an axis passing through its mid point with the angular velocity ω. Hence the force exerted by one half on the other = mass of one half x acceleration of C.M. of that part, in the frame of C.M
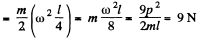
Q. 274. A thin uniform square plate with side l and mass M can rotate freely about a stationary vertical axis coinciding with one of its sides. A small ball of mass m flying with velocity v at right angles to the plate strikes elastically the centre of it. Find:
(a) the velocity of the ball v' after the impact;
(b) the horizontal component of the resultant force which the axis will exert on the plate after the impact.
Solution. 274. (a) In the process of motion of the given system the kinetic energy and the angular momentum relative to rotation axis do not vary. Hence it follows that
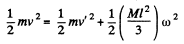
and 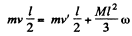
From these equations we obtain
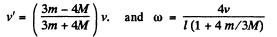
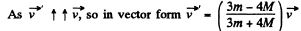
(b) Obviously the sought force provides the centripetal acceleration to the C.M. of the rod and is

Q. 275. A vertically oriented uniform rod of mass M and length l can rotate about its upper end. A horizontally flying bullet of mass m strikes the lower end of the rod and gets stuck in it; as a result, the rod swings through an angle α. Assuming that m << M, find:
(a) the velocity of the flying bullet;
(b) the momentum increment in the system "bullet-rod" during the impact; what causes the change of that momentum;
(c) at what distance x from the upper end of the rod the bullet must strike for the momentum of the system "bullet-rod" to remain constant during the impact.
Solution. 275. (a) About the axis of rotation of the rod, the angular momentum of the system is conserved. Thus if the velocity of the flying bullet is v.
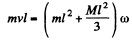
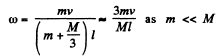 (1)
(1)
Now from the conservation of mechanical energy of-the system (rod with bullet) in the uniform field of gravity
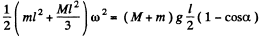 (2)
(2)
[because C.M. of rod raises by the height 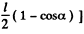
Solving (1) and (2), we get
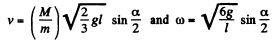
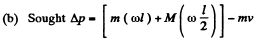
where , ωl is the velqcdty of the bullet and 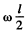 equals the velocity of C.M. of the rod after the impact. Putting the value of v and ω we get
equals the velocity of C.M. of the rod after the impact. Putting the value of v and ω we get
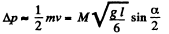
This is caused by the reaction at the hinge on the upper end.
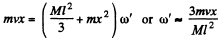
Final momentum is
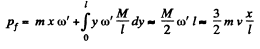
So, 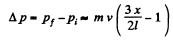
This vanishes for 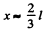
Q. 276. A horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body. Initially the body was located at the edge of the disc and the whole system rotated with an angular velocity ω0. Then by means of a force F applied to the lower end of the thread the body was slowly pulled to the rotation axis. Find:
(a) the angular velocity of the system in its final state;
(b) the work performed by the force F.
Solution. 276. (a) As force F on the body is radial so its angular momentum about the axis becomes zero and the angular momentum of the system about the given axis is conserved. Thus
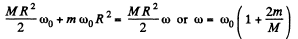
(b) From the equation of the increment of the mechanical energy of the system :
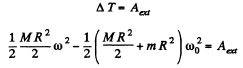
Putting the value of ω from part (a) and solving we get
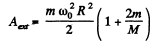
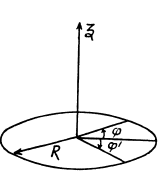
Q. 277. A man of mass ml stands on the edge of a horizontal uniform disc of mass m2 and radius R which is capable of rotating freely about a stationary vertical axis passing through its centre. At a cer- tain moment the man starts moving along the edge of the disc; he shifts over an angle φ' relative to the disc and then stops. In the process of motion the velocity of the man varies with time as v' (t). Assuming the dimensions of the man to be negligible, find:
(a) the angle through which the disc had turned by the moment the man stopped;
(b) the force moment (relative to the rotation axis) with which the man acted on the disc in the process of motion.
Solution. 277. (a) Let z be the rotation axis of disc and <p be its rotation angle in accordance with right-hand screw rule (Fig.). (φ and φ' are to be measured in the same sense algebraically.) As Mz of the system (disc + man) is conserved and  we have at any instant,
we have at any instant,
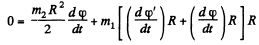
or, 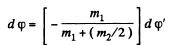
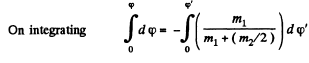
or, 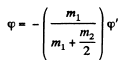 (1)
(1)
This gives the total angle of rotation of the disc.

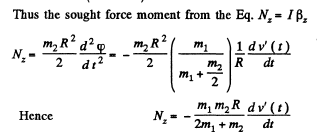
Q. 278. Two horizontal discs rotate freely about a vertical axis passing through their centres. The moments of inertia of the discs relative to this axis are equal to l1 and l2, and the angular velocities to oh and ω1. When the upper disc fell on the lower one, both discs began rotating, after some time, as a single whole (due to friction). Find:
(a) the steady-state angular rotation velocity of the discs;
(b) the work performed by the friction forces in this process.
Solution. 278. (a) Frome the law of conservation of angular momentum of the system relative to vertical axis z, it follows that:
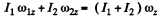
Hence 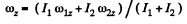
Not that for ωz > 0, the corresponding vector  with the poitive direction to the z axis, and vice versa. As both discs rotates about the same vertical axis z, thus in vector form.
with the poitive direction to the z axis, and vice versa. As both discs rotates about the same vertical axis z, thus in vector form.
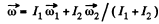
However, the problem makes sense only if 
(b) From the equation of increment of mechanical energy of a system: 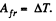
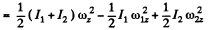
Using Eq. (1)
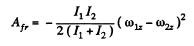
Q. 279. A small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horizontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
Solution. 279. For the closed system (disc + rod), the angular momentum is conserved about any axis. Thus from the conservation of angular momentum of the system about the rotation axis of rod passing through its C.M. gives :
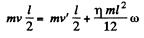 (1)
(1)
(v' is the final velocity of the disc and co angular velocity of the rod) For the closed system linear momentum is also conserved. Hence
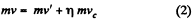
(where vc is the velocity of C.M. of the rod) From Eqs (1) and (2) we get


Applying conservation of kinetic energy, as the collision is elastic

Vectorially, noting that we have taken 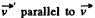
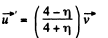
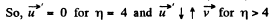
Q. 280. A stationary platform P which can rotate freely about a vertical axis (Fig. 1.72) supports a motor M and a balance weight N. The mo- ment of inertia of the platform with the motor and the balance weight relative to this axis is equal to I. A light frame is fixed to the motor's shaft with a uniform sphere A rotating freely with an angular velocity ω0 about a shaft BB' coinciding with the axis OO'. The moment of inertia of the sphere relative to the rotation axis is equal to I. Find:
(a) the work performed by the motor in turning the shaft BB' through 90'; through 180°;
(b) the moment of external forces which maintains the axis of the arrangement in the vertical position after the motor turns the shaft BB' through 90°.
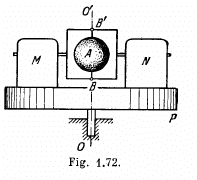
Solution. 280. See the diagram in the book (Fig. 1.72) (a) When the shaft BB' is turned through 90° the platform must start turning with angular velocity Ω so that the angular momentum remains constant. Here
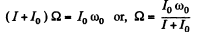
The work performed by the motor is therefore
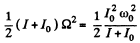
If the shaft is turned through 180°, angular velocity of the sphere changes sign. Thus from conservation of angular momentum,
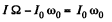
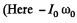 is the complete angular momentum of the sphere i. e. we assume that the angular velocity of the sphere is just - ω0). Then
is the complete angular momentum of the sphere i. e. we assume that the angular velocity of the sphere is just - ω0). Then
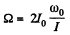
and the work done must be,
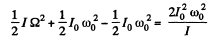
(b) In the case (a), first part, the angular momentum vector of the sphere is precessing with angular velocity Ω. Thus a torque,
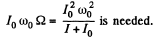
FAQs on Irodov Solutions: Dynamics of A Solid Body- 3 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the concept of dynamics in the context of a solid body? |  |
| 2. How does the study of dynamics help in understanding the behavior of a solid body? |  |
| 3. What are some common examples where the principles of dynamics are applicable to solid bodies? |  |
| 4. How can one solve problems related to the dynamics of a solid body? |  |
| 5. What are the practical applications of studying dynamics in the context of solid bodies? |  |
















