Irodov Solutions: Elastic Waves. Acoustics- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.150. How long will it take sound waves to travel the distance l between the points A and B if the air temperature between them varies linearly from T1 to T2? The velocity of sound propagation in air is equal to 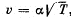 where a is a constant.
where a is a constant.
Ans. Since the tempeiature varies linearly we can write the temperature as a function of x, which is, the distance from the point A towards B.
i.e., 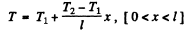
hence, 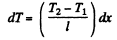 (1)
(1)
In order to travel an elemental distance of dx which is at a distance of x from A it will take a time
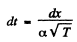 (2)
(2)
From Eqns (1) and (2), expressing dx in terms of dT, we get
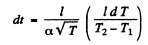
Which on integration gives
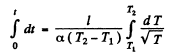
or,
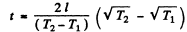
Hence the sought time 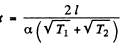
Q.151. A plane harmonic wave with frequency ω propagates at a velocity v in a direction forming angles α, β, γ with the x, y, z axes. Find the phase difference between the oscillations at the points of medium with coordinates x1, y1, z1 a nd x2, y2, z2.
Ans. Equation of plane wave is given by
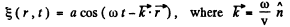 called the wave vector and
called the wave vector and 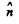 is the unit vector normal to the wave surface in the direction of the propagation of wave.
is the unit vector normal to the wave surface in the direction of the propagation of wave.
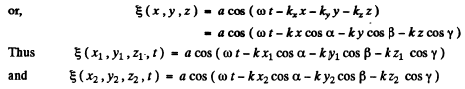
Hence the sought wave phase difference
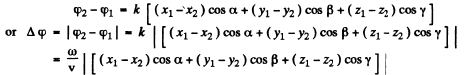
Q.152. A plane wave of frequency ω propagates so that a certain phase of oscillation moves along the x, y, z axes with velocities v1, v2, v3 respectively. Find the wave vector k, assuming the unit vectors ex, ey, ez of the coordinate axes to be assigned.
Ans. The phase of the oscillation can be written as
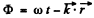
When the wave moves along the x-axis
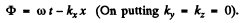
Since the velocity associated with this wave is v1
We have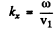
Similarly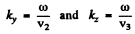
Thus 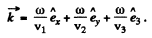
Q.153. A plane elastic wave 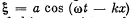 propagates in a medium K. Find the equation of this wave in a reference frame K' moving in the positive direction of the x axis with a constant velocity V relative to the medium K. Investigate the expression obtained.
propagates in a medium K. Find the equation of this wave in a reference frame K' moving in the positive direction of the x axis with a constant velocity V relative to the medium K. Investigate the expression obtained.
Ans. The wave equation propagating in the direction of +ve x axis in medium K is give as
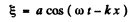
So, 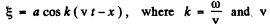 is the wave velocity
is the wave velocity
In the refrence frame K' , the wave velocity will be ( v - V ) propagating in the direction of +ve x axis and x will be x'. Thus the sought wave equation.
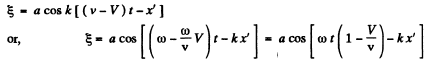
Q.154. Demonstrate that any differentiable function f (t + ax), where a is a constant, provides a solution of wave equation. What is the physical meaning of the constant α?
Ans. This follows on actually putting
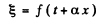
in the wave equation
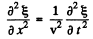
(We have written the one dimensional form of the wave equation.) Then
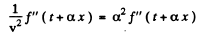
so the wave equation is satisfied if
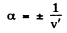
That is the physical meaning of the constant α .
Q.155. The equation of a travelling plane sound wave has the form  = 60 cos (1800t — 5.3x), where
= 60 cos (1800t — 5.3x), where is expressed in micrometres, t in seconds, and x in metres. Find:
is expressed in micrometres, t in seconds, and x in metres. Find:
(a) the ratio of the displacement amplitude, with which the particles of medium oscillate, to the wavelength;
(b) the velocity oscillation amplitude of particles of the medium and its ratio to the wave propagation velocity;
(c) the oscillation amplitude of relative deformation of the medium and its relation to the velocity oscillation amplitude of particles of the medium.
Ans. The given wave equation
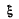 = 60 cos (1800t — 5.3x)
= 60 cos (1800t — 5.3x)
is of the type
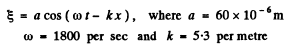
As 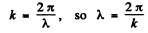
and also 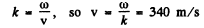
(a) Sought ratio 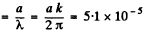
(b) Since
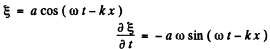
So velocity oscillation amplitude
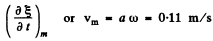 (1)
(1)
and the sought ratio of velocity oscillation amplitude to the wave propagation velocity
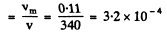
(c) Relative deformation 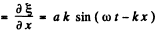
So, relative deformation amplitude
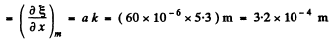 (2)
(2)
From Eqns (1 ) and (2)
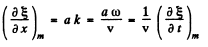
Thus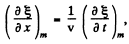 where v = 340 m/s is the wave velocity.
where v = 340 m/s is the wave velocity.
Q.156. A plane wave 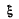 = a cos (ωt — kx) propagates in a homogeneous elastic medium. For the moment t = 0 draw
= a cos (ωt — kx) propagates in a homogeneous elastic medium. For the moment t = 0 draw
(a) the plots of 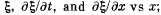
(b) the velocity direction of the particles of the medium at the points where 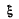 = 0, for the cases of longitudinal and transverse waves;
= 0, for the cases of longitudinal and transverse waves;
(c) the approximate plot of density distribution p (x) of the medium for the case of longitudinal waves.
Ans. (a) The given equation is,
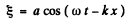
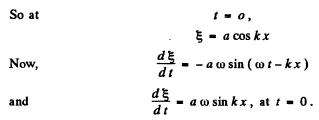
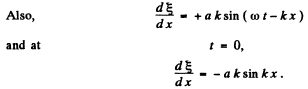
Hence all the graphs are similar having different amplitudes, as shown in the answer- sheet of the problem book.
(b) At the points, where 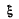 = 0, the velocity direction is positive, i.e., along + ve x - axis in the case of longitudinal and + ve y- axis in the case of transverse waves, where
= 0, the velocity direction is positive, i.e., along + ve x - axis in the case of longitudinal and + ve y- axis in the case of transverse waves, where 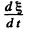 is positive and vice versa.
is positive and vice versa.
For sought plots see the answer-sheet of the problem book.
Q.157. A plane elastic wave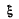 = ae -Yx cos (ωt — kx), where a, γ, ω, and k are constants, propagates in a homogeneous medium. Find the phase difference between the oscillations at the points where the particles' displacement amplitudes differ by η = 1.0%, if γ = = 0.42 m -1 and the wavelength is γ = 50 cm.
= ae -Yx cos (ωt — kx), where a, γ, ω, and k are constants, propagates in a homogeneous medium. Find the phase difference between the oscillations at the points where the particles' displacement amplitudes differ by η = 1.0%, if γ = = 0.42 m -1 and the wavelength is γ = 50 cm.
Ans. In the given wave equation the particle’s displacement amplitude = ae -yx
Let two points x1 and x2 , between which the displacement amplitude differ by η = 1 %
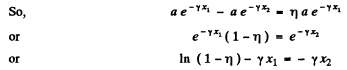
or, 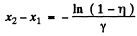
So path difference 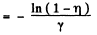
and phase different 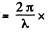 path difference
path difference
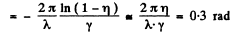
Q.158. Find the radius vector defining the position of a point source of spherical waves if that source is known to be located on the straight line between the points with radius vectors r1 and r2 at which the oscillation amplitudes of particles of the medium are equal to al and a2. The damping of the wave is negligible, the medium is homogeneous.
Ans. Let S be the source whose position vector relative to the reference point O is 
Since intensities are inversely proportional to the square of distances,
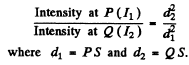
But intensity is proportional to the square of amplitude.
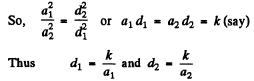
Let 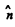 be the unit vector along PQ directed from P to Q.
be the unit vector along PQ directed from P to Q.
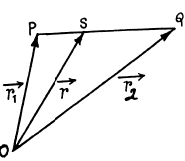
Then 
and 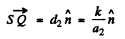
From the triangle law of vector addition.
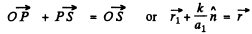
or 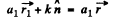 (1)
(1)
Similarly  (2)
(2)
Adding (1) and (2),
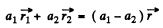
Hence 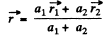
Q.159. A point isotropic source generates sound oscillations with frequency v = 1.45 kHz. At a distance r, = 5.0 m from the source the displacement amplitude of particles of the medium is equal to a0 = 50 pm, and at the point A located at a distance r = 10.0 m from the source the displacement amplitude is η = 3.0 times less than a0. Find:
(a) the damping coefficient γ of the wave;
(b) the velocity oscillation amplitude of particles of the medium at the point A.
Ans. (a) We know that the equation of a spherical wave in a homogeneous absorbing medium of wave damping coefficient γ is :
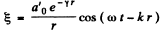
Thus particle’s displacement amplitude equals
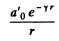
According to the conditions of the problem,
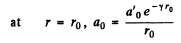 (1)
(1)
and when 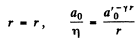 (2)
(2)
Thus from Eqns (1) and (2)
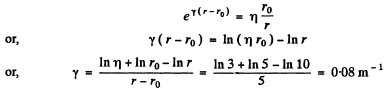
(b)
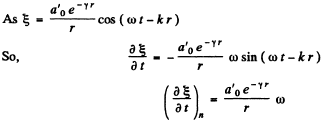
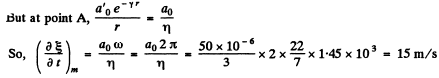
Q.160. Two plane waves propagate in a homogeneous elastic medium, one along the x axis and the other along the y axis:  1 = = a cos (ωt - kx),
1 = = a cos (ωt - kx), 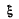 2 = a cos (wt - ky). Find the wave motion pattern of particles in the plane xy if both waves
2 = a cos (wt - ky). Find the wave motion pattern of particles in the plane xy if both waves
(a) are transverse and their oscillation directions coincide;
(b) are longitudinal.
Ans. (a) Equation of the resultant wave,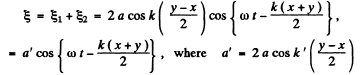
Now, the equation of wave pattern is,
x + y = k , (a Const.)
For sought plots see the answer-sheet of the problem book.
For antinodes, i.e. maximum intensity
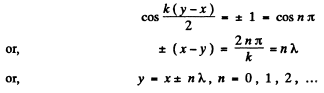
Hence, the particles of the medium at the points, lying on the solid straight lines 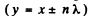 , oscillate with maximum amplitude.
, oscillate with maximum amplitude.
For nodes, i.e. minimum intensity,
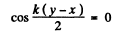
or,

or, 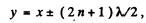
and hence the particles at the points, lying on dotted lines do not oscillate.
(b) When the waves are longitudinal,
For sought plots see the answer-sheet of the problem book.
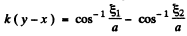

from (1), if
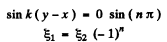
thus, the particles o f the medium at the points lying on the straight lines,  will oscillate along those lines (even n), or at right angles to them (odd n).
will oscillate along those lines (even n), or at right angles to them (odd n).
Also from (1),
if
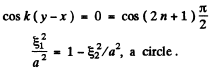
Thus the particles, at the points, where 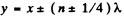 will oscillate along circles.
will oscillate along circles.
In general, all other particles will move along ellipses.
Q.161. A plane undamped harmonic wave propagates in a medium. Find the mean space density of the total oscillation energy (w), if at any point of the medium the space density of energy becomes equal to w0 one-sixth of an oscillation period after passing the displacement maximum.
Ans. The displacement of oscillations is given by 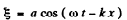
Without loss of generality, we confine ourselves to x = 0. Then the displacement maxima occur at ωt = nπ. Concentrate at ωt = 0 . Now the energy density is given by
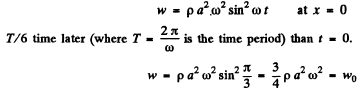
Thus
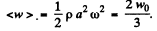
Q.162. A point isotropic sound source is located on the perpendicular to the plane of a ring drawn through the centre 0 of the ring. The distance between the point 0 and the source is l = 1.00 m, the radius of the ring is R = 0.50 m. Find the mean energy flow across the area enclosed by the ring if at the point 0 the intensity of sound is equal to l0 = 30 µW/m2. The damping of the waves is negligible.
Ans. The power output of the source much be
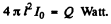
The required flux of accoustic power is then : 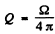
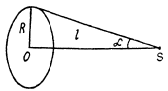
Where Ω is the solid angle subtended by the disc enclosed by the ring at S. This solid angle is
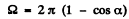
So flux 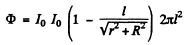
Substitution gives 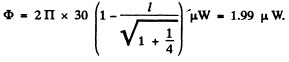
Eqn. (1) is a well known result stich is derived as follows; Let SO be the polar axis. Then the required solid angle is the area of that part of the surface a sphere of much radius whose colatitude is ≤ α.
Thus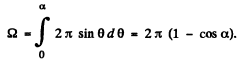
Q.163. A point isotropic source with sonic power P = 0.10 W is located at the centre of a round hollow cylinder with radius R = = 1.0 m and height h = 2.0 m. Assuming the sound to be completely absorbed by the walls of the cylinder, find the mean energy flow reaching the lateral surface of the cylinder.
Ans. From the result of 4.162 power flowing out through anyone of the opening
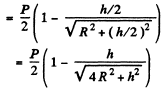
As total power output equals P, so the power reaching the lateral surface must be.
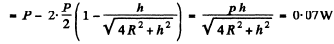
Q.164. The equation of a plane standing wave in a homogeneous elastic medium has the form 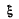 = a cos kx• cos wt. Plot:
= a cos kx• cos wt. Plot:
(a) 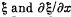 as functions of x at the moments t = 0 and t = T/2, where T is the oscillation period;
as functions of x at the moments t = 0 and t = T/2, where T is the oscillation period;
(b) the distribution of density p (x) of the medium at the moments t = 0 and t = T/2 in the case of longitudinal oscillations;
(c) the velocity distribution of particles of the medium at the moment t = T/4; indicate the directions of velocities at the antinodes, both for longitudinal and transverse oscillations.
Ans. We are given
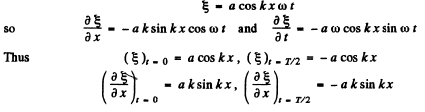
(a) The graphs of 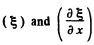 are as shown in Fig. (35) of the book (p.332).
are as shown in Fig. (35) of the book (p.332).
(b) We can calculate the density as follows :
Take a parallelopiped of cross section unity and length dx with its edges at x and x + dx.
After the oscillation the edge at x goes to x + 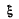 ( x) and the edge at x + d x goes to
( x) and the edge at x + d x goes to
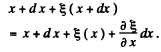 Thus the volume of the element (originally dx) becomes
Thus the volume of the element (originally dx) becomes
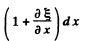
and hence the density becomes 
On substituting we get for the density p (x) the curves shown in Fig.(35). referred to above.
(c) The velocity v (x) at time t = T/4 is
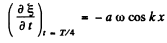
On plotting we get the figure (36).
Q.165. A longitudinal standing wave 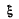 = a cos kx- cos wt is maintained in a homogeneous medium of density ρ. Find the expressions for the space density of
= a cos kx- cos wt is maintained in a homogeneous medium of density ρ. Find the expressions for the space density of
(a) potential energy wp (x, t);
(b) kinetic energy wk (x, t).
Plot the space density distribution of the total energy w in the space between the displacement nodes at the moments t = 0 and t = T/4, where T is the oscillation period.
Ans. Given 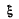 = a cos kx- cos wt
= a cos kx- cos wt
(a) The potential eneigy density (per unit volume) is the eneigy of longitudinal strain. This is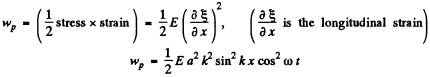
But 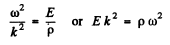
Thus 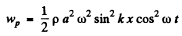
(b) The kinetic energy density is
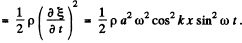
On plotting wc get Fig. 37 given in the book (p. 332). For example at t = 0
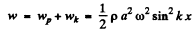
and the displacement nodes are at 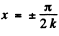 so we do get the figure.
so we do get the figure.
Q.166. A string 120 cm in length sustains a standing wave, with the points of the string at which the displacement amplitude is equal to 3.5 mm being separated by 15.0 cm. Find the maximum displacement amplitude. To which overtone do these oscillations correspond?
Ans. Let us denote the displacement of the elements of the string by
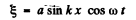
since the string is 120 cm long we must have k.120 = n π
If X1 is the distance at which the displacement amplitude first equals 3.5 mm then
Then 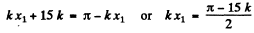
One can convince ourself that the string has the form shown below
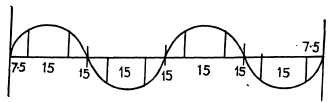
It shows that 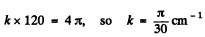
Thus we are dealing with the third overtone
Also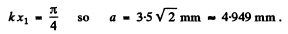
Q.167. Find the ratio of the fundamental tone frequencies of two identical strings after one of them was stretched by η1 = 2.0% and the other, by η2 = 4.0%. The tension is assumed to 'be proportional to the elongation.
Ans. We have 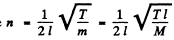 here M = total mass of the wire. When the write is stretched, total mass of the wire remains constant. For the first wire the new length = l + η1 l and for the record wire, the length is l+ η2l. Also T1 = α(η1 l) where α is a constant and T2 = α (η2l) . Substituting in the above formula.
here M = total mass of the wire. When the write is stretched, total mass of the wire remains constant. For the first wire the new length = l + η1 l and for the record wire, the length is l+ η2l. Also T1 = α(η1 l) where α is a constant and T2 = α (η2l) . Substituting in the above formula.
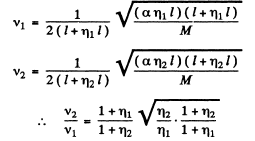
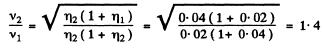
Q.168. Determine in what way and how many times will the fundamental tone frequency of a stretched wire change if its length is shortened by 35% and the tension increased by 70%.
Ans. Let initial length and tension be l and T respectively.
So, 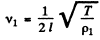
In accordance with the problem, the new length
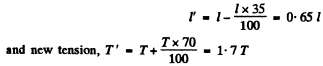
Thus the new frequency
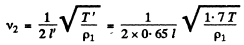
Hence 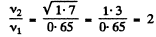
Q.169. To determine the sound propagation velocity in air by acoustic resonance technique one can use a pipe with a piston and a sonic membrane closing one of its ends. Find the velocity of sound if the distance between the adjacent positions of the piston at which resonance is observed at a frequency v = 2000 Hz is equal to l = = 8.5 cm.
Ans. Obviously in this case the velocityof sound propagation
v - 2v ( /2 - l1)
where l2 and l1 are consecutive lengths at which resonance occur
In our problem,
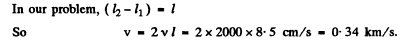
Q.170. Find the number of possible natural oscillations of air column in a pipe whose frequencies lie below v, = 1250 Hz. The length of the pipe is l = 85 cm. The velocity of sound is v = 340 m/s. Consider the two cases:
(a) the pipe is closed from one end;
(b) the pipe is opened from both ends. The open ends of the pipe are assumed to be the antinodes of displacement.
Ans. (a) When the tube is closed at one end
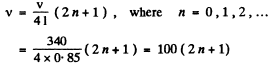
Thus for
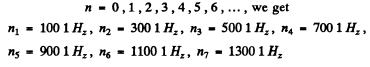
Since v should be < v0 = 1250 1Hz we need not go beyond n6.
Thus 6 natural oscillations are possible.
(b) Organ pipe opened from both ends vibrateb with all harmonics of the fundamental frequency. Now, the fundamental mode frequency is given as
v = v/λ
or, v = v/2l Here, also, end correction has been neglected. So, the frequencies of higher modes of vibrations are given by
v = n ( v/2l) (1)
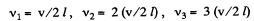
It may be checked by putting the values of n in the equation (1) that below 1285 Hz, there are a total of six possible natural oscillation frequencies of air column in the open pipe.
FAQs on Irodov Solutions: Elastic Waves. Acoustics- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are elastic waves in acoustics? |  |
| 2. How do elastic waves propagate in different mediums? |  |
| 3. What is the significance of elastic waves in acoustics? |  |
| 4. What factors affect the speed of elastic waves in a medium? |  |
| 5. How are elastic waves used in non-destructive testing? |  |


















