Irodov Solutions: Elastic Waves. Acoustics- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.171. A copper rod of length l = 50 cm is clamped at its midpoint. Find the number of natural longitudinal oscillations of the rod in the frequency range from 20 to 50 kHz. What are those frequencies equal to?
Ans. Since the copper rod is clamped at mid point, it becomes a mode and the two free ends will be anitinodes. Thus the fundamental mode formed in the rod is as^shown in the Fig. (a).
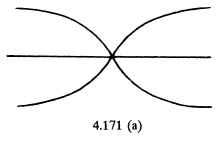
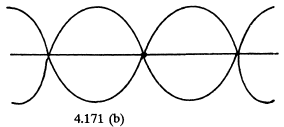
in this case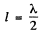
So,
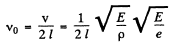
where E = Young’s modules and p is the density of the copper
Similarly the second mode or the first overtone in the rod is as shown above in Fig. (b).
Here 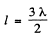
Hence
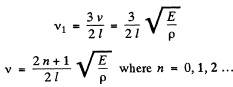
Putting the given values of E and p in the general equation

Hence the sought number of frequencies between 20 to 50 k Hz equals 4.
Q.172. A string of mass rn, is fixed at both ends. The fundamental tone oscillations are excited with circular frequency ω and maximum displacement amplitude amax. Find:
(a) the maximum kinetic energy of the string;
(b) the mean kinetic energy of the string averaged over one oscillation period.
Ans. Let two waves 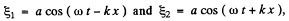 superpose and as a result, we have a standing wave (the resultant wave ) in the string of the form
superpose and as a result, we have a standing wave (the resultant wave ) in the string of the form 
According to the problem 2 a = am.
Hence the standing wave excited in the string is
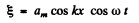 (1)
(1)
or, 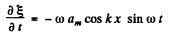 (2)
(2)
So the kinetic energy confined in the string element of length dx, is given by
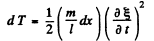
or, 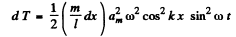
or, 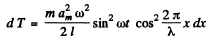
Hence the kinetic energy confined in the string corresponding to the fundamental tone
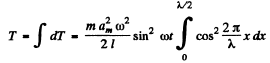
Because, for the fundamental tone, length of the string 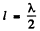
Integrating we get, 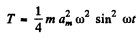
Hence the sought maximum kinetic energy equals, 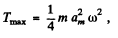
because for 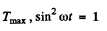
(ii) Mean kinetic energy averaged over one oscillation period
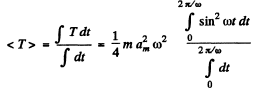
or, 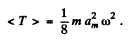
Q.173. A standing wave 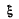 = a sin kx•cos cot is maintained in a homogeneous rod with cross-sectional area S and density p. Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
= a sin kx•cos cot is maintained in a homogeneous rod with cross-sectional area S and density p. Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
Ans. We have a standing wave given by the equation

The kinetic energy confined in an element of length dx of the rod
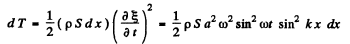
So total kinetic energy confined into rod
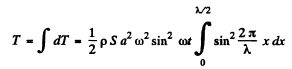
or,  (3)
(3)
The potential energy in the above rod element
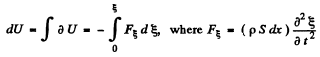
or,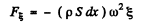
so, 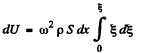
or, 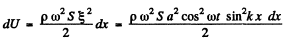
Thus the total potential energy stored in the rod 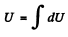
or, 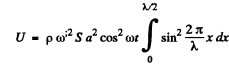
so, 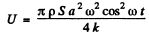
To find the potential energy stored in the rod element we may adopt an easier way. We know that the potential energy density confined in a rod under elastic force equals :
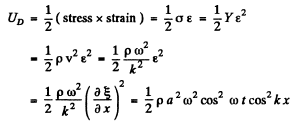
Hence the total potential energy stored in the rod
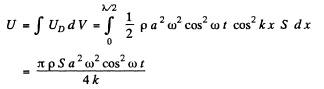
Hence the sought mechanical energy confined in the rod between the two adjacent nodes
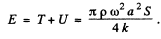
Q.174. A source of sonic oscillations with frequency vo = 1000 Hz moves at right angles to the wall with a velocity u = 0.17 m/s. Two stationary receivers R1 and R2 are located on a straight line, coinciding with the trajectory of the source, in the following succession: R1-source-R2-wall. Which receiver registers the beatings and what is the beat frequency? The velocity of sound is equal to v = 340 m/s.
Ans. Receiver R1 registers the beating, due to the sound waves reaching directly to it from source and the other due to the reflection from the wall.
Frequency of sound reaching directly from S to R1
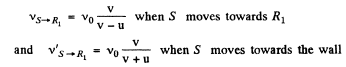
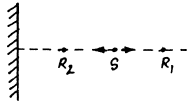
Now frequency reaching to R1 after reflection from wall
Thus the sought beat frequency
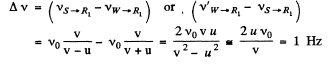
Q.175. A stationary observer receives sonic oscillations from two tuning forks one of which approaches, and the other recedes with the same velocity. As this takes place, the observer hears the beatings with frequency v = 2.0 Hz. Find the velocity of each tuning fork if -their oscillation frequency is vo = 680 Hz and the velocity of sound in air is v = 340 m/s.
Ans. Let the velocity of tuning fork is u. Thus frequency reaching to the observer due to the tuning fork that approaches the observer
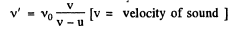
Frequency reaching the observer due to the tunning fork that recedes from the observer
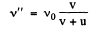

Hence 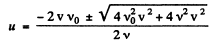
Hence the sought value of u, on sim plifying and noting that u > 0
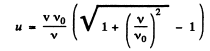
Q.176. A receiver and a source of sonic oscillations of frequency vo = 2000 Hz are located on the x axis. The source swings harmonically along that axis with a circular frequency ω and an amplitude a = 50 cm. At what value of ω will the frequency bandwidth registered by the stationary receiver be equal to Av = 200 Hz? The velocity of sound is equal to v = 340 m/s.
Ans. Obviously the maximum, frequency will be heard when the source is moving with maximum velocity towards the receiver and minimum frequency will be heard when the source recedes with maximum velocity. As the source swing harmonically its maximum velocity equals ω to. Hence
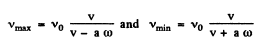
So the frequency band width 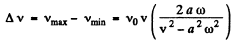

On simplifying (and taking + sign as 
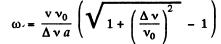
Q.177. A source of sonic oscillations with frequency vo = 1700 Hz and a receiver are located at the same point. At the moment t = 0 the source starts receding from the receiver with constant acceleration w = 10.0 m/s2. Assuming the velocity of sound to be equal to v = 340 m/s, find the oscillation frequency registered by the stationary receiver t = 10.0 s after the start of motion.
Ans. It should be noted that the frequency emitted by the source at time t could not be received at the same moment by the receiver, becouse till that time the source will cover the distance 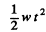 and the sound wave will take the further time
and the sound wave will take the further time 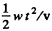 to reach the receiver. Therefore the frequency noted by the receiver at time t should be emitted by the source at the time
to reach the receiver. Therefore the frequency noted by the receiver at time t should be emitted by the source at the time 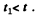 Therefore
Therefore
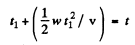 (1)
(1)
and the frequency noted by the receiver
 (2)
(2)
Solving Eqns (1) and (2), we get
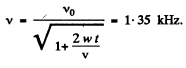
Q.178. A source of sound with natural frequency vo = 1.8 kHz moves uniformly along a straight line separated from a stationary observer by a distance l = 250 m. The velocity of the source is equal to η = 0.80 fraction of the velocity of sound. Find:
(a) the frequency of sound received by the observer at the moment when the source gets closest to him;
(b) the distance between the source and the observer at the moment when the observer receives a frequency v = vo.
Ans. (a) When the observer receives the sound, the source is closest to him. It means, that frequency is emitted by the source sometimes before (Fig.) Figure shows that the source approaches the stationary observer with
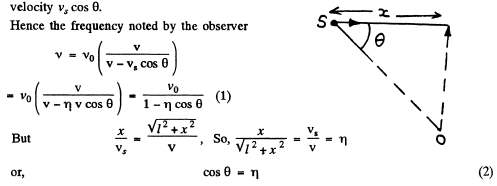
Hence from Eqns. (1) and (2) the sought frequency
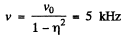
(b) When the source is right in front of O, the sound emitted by it will not be Doppler shifted because 0 = 90°. This sound will be received at O at time  after the source has v passed it. The source will by then have moved ahead by a distance
after the source has v passed it. The source will by then have moved ahead by a distance 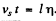 . The distance between the source and the observer at this time will be
. The distance between the source and the observer at this time will be 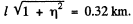
Q.179. A stationary source sends forth monochromatic sound. A wall approaches it with velocity u = 33 cm/s. The propagation velocity of sound in the medium is v = 330 m/s. In what way and how much, in per cent, does the wavelength of sound change on reflection from the wall?
Ans. Frequency of sound when it reaches the wall
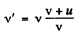
wall will reflect the sound with same frequency v'. Thus frequency noticed by a stationary observer after reflection from wall
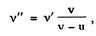 since wall behaves as a source o f frequency v'
since wall behaves as a source o f frequency v'
 .
.
Hence the sought percentage change in wavelength
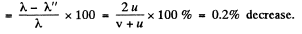
Q.180. A source of sonic oscillations with frequency vo = 1700 Hz and a receiver are located on the same normal to a wall. Both the source and the receiver are stationary, and the wall recedes from the source with velocity u = 6.0 cm/s. Find the beat frequency registered by the receiver. The velocity of sound is equal to'. v = 340 m/s.
Ans. Frequency of sound reaching the wall.
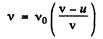 (1)
(1)
Now for the observer the wall becomes a source of frequency v receding from it with velocity u Thus, the frequency reaching the observer
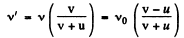 [Using (1)]
[Using (1)]
Hence the beat frequency registered by the receiver (observer)

Q.181. Find the damping coefficient y of a sound wave if at distances r1 = 10 m and r2 = 20 m from a point isotropic source of sound the sound wave intensity values differ by a factor η = 4.5.
Ans. Intensity of a spherical sound wave emitted from a point source in a homogeneous absorbing medium of wave damping coefficient y is given by
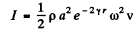
So, Intensity of sound at a distance r1 from the source
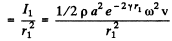
and intensity of sound at a distance r2 from the source
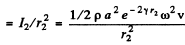
But according to the problem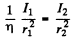
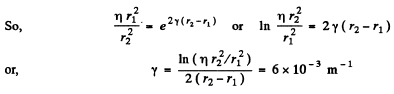
Q.182. A plane sound wave propagates along the x axis. The damping coefficient of the wave is γ = 0.0230 m-1. At the point x = 0 the loudness level is L = 60 dB. Find:
(a) the loudness level at a point with coordinate x = 50 m;
(b) the coordinate x of the point at which the sound is not heard any more.
Ans. (a)Loudness level in bells 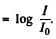 (I0 is the theshold o f audibility.)
(I0 is the theshold o f audibility.)
So, loudness level in decibells, 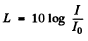
Thus loudness level at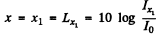
Similarly 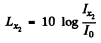
Thus 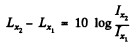

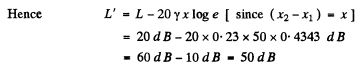
(b) The point at which the sound is not heard any more, the loudness level should be zero.
Thus
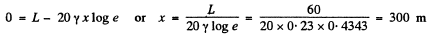
Q.183. At a distance ro = 20.0 m from a point isotropic source of sound the loudness level Lo = 30.0 dB. Neglecting the damping of the sound wave, find:
(a) the loudness level at a distance r = 10.0 m from the source;
(b) the distance from the source at which the sound is not heard.
Ans. (a) As there is no damping, so
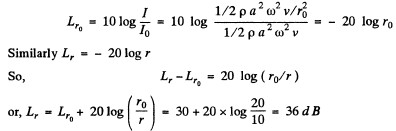
(b) Let r be the sought distance at which the sound is not heard.
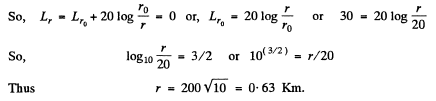
Thus for r > 0. 63 km no sound will be heard.
Q.184. An observer A located at a distance ζA = 5,0 m from a ringing tuning fork notes the sound to fade away ζ= 19 s later than an observer B who is located at a distance ζB = 50 m from the tuning fork. Find the damping coefficient β of `Oscillations of the tuning fork. The sound velocity v = 340 m/s.
Ans. We treat the fork as a point source. In the absence of damping the oscillation has the form
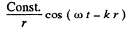
Because of the damping of the fork the amplitude of oscillation decreases exponentially with the retarded time (i.e. the time at which the wave started from the source.). Thus we write for the wave amplitude.
This means that
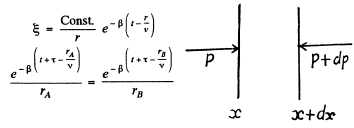
Thus 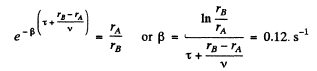
Q.185. A plane longitudinal harmonic wave propagates in a medium with density ρ. The velocity of the wave propagation is v. Assuming that the density variations of the medium, induced by the propagating wave, Aρ ≪ ρ, demonstrate that
(a) the pressure increment in the medium 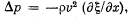 where
where 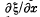 is the relative deformation;
is the relative deformation;
(b) the wave intensity is defined by Eq. (4.3i).
Ans. (a) Let us consider the motion of an element of the medium of thickness dx and unit area of cross-section. Let 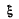 displacement of the particles of the medium at location x. Then by the equation of motion
displacement of the particles of the medium at location x. Then by the equation of motion
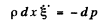
where dp is the pressure increment over the length dx
Recalling the wave equation
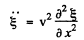
we can write the foregoing equation as
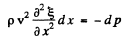
Integrating this equation, we get

In the absence of a deformation (a wave), the surplus pressure is Δp = 0. So ’Const’ = 0 and
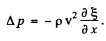
(b) We have found earlier that
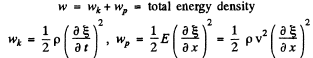
It is easy m see that the space-time average of both densities is the same and the space time average of total energy density is then
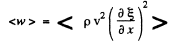
The intensity of the wave is
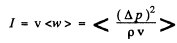
Using
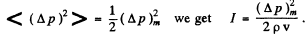
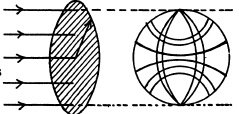
Q.186. A ball of radius R = 50 cm is located in the way of propagation of a plane sound wave. The sonic wavelength is λ = 20 cm, the frequency is v = 1700 Hz, the pressure oscillation amplitude in air is (Δp)m = 3.5 Pa. Find the mean energy flow, averaged over an oscillation period, reaching the surface of the ball.
Ans. The intensity of the sound wave is
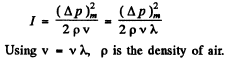
Thus the mean eneigy flow reaching the ball is
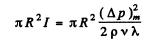
 being the effective area (area of cross section) of the ball. Substitution gives 10.9 mW.
being the effective area (area of cross section) of the ball. Substitution gives 10.9 mW.
Q.187. A point A is located at a distance r = 1.5 m from a point isotropic source of sound of frequency v = 600 Hz. The sonic power of the source is P = 0.80 W. Neglecting the damping of the waves and assuming the velocity of sound in air to be equal to v = 340 m/s, find at the point A:
(a) the pressure oscillation amplitude (Δp)m and its ratio to the air pressure;
(b) the oscillation amplitude of particles of the medium; compare it with the wavelength of sound.
Ans.
(b) We have
Q.188. At a distance r = 100 m from a point isotropic source of sound of frequency 200 Hz the loudness level is equal to L = 50 dB. The audibility threshold at this frequency corresponds to the sound intensity l0 = 0.10 nW/m2. The damping coefficient of the sound wave is γ = 5.0.10-4 m-1. Find the sonic power of the source.
Ans. Express L in bels. (i.e. L = 5 bels).
Then the intensity at the relevant point (at a distance r from the source) is 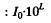
Had there been no damping the intensity would have been 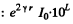
Now this must equal the quantity
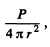 where P = sonic power of the source.
where P = sonic power of the source.
Thus 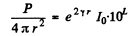
or 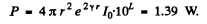
FAQs on Irodov Solutions: Elastic Waves. Acoustics- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are elastic waves in acoustics? |  |
| 2. How do elastic waves propagate through a medium? |  |
| 3. What is the relationship between the frequency and wavelength of elastic waves in acoustics? |  |
| 4. How are elastic waves generated in acoustics? |  |
| 5. What are the applications of elastic waves in acoustics? |  |


















