Irodov Solutions: Electric Capacitance Energy of an Electric Field - 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 117. A circuit has a section AB shown in Fig. 3.21. The emf of the source equals 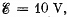 the capacitor capacitances are equal to C1 = 1.0 μF and C2 = 2.0 μF, and the potential difference φA - φB = 5.0 V. Find the voltage across each capacitor.
the capacitor capacitances are equal to C1 = 1.0 μF and C2 = 2.0 μF, and the potential difference φA - φB = 5.0 V. Find the voltage across each capacitor.
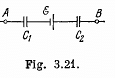
Solution. 117. Let, us make the charge distribution, as shown in the figure.
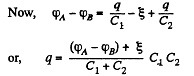

Hence, voltage across the capacitor C1
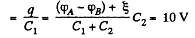
and voltage across the capacitor, C2
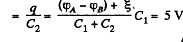
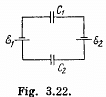
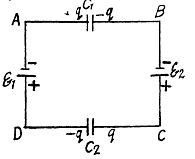
Q. 118. In a circuit shown in Fig. 3.22 find the potential difference between the left and right plates of each capacitor.
Solution. 118.  then using
then using  in the closed circuit, (Fig.)
in the closed circuit, (Fig.)

or, 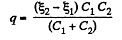
Hence the P.D. accross the left and right plates of capacitors,
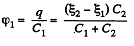
and similarly
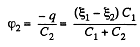
Q. 119. Find the charge of each capacitor in the circuit shown in Fig. 3.22.

Solution. 119. Taking benefit of tBe foregoing problem, the amount of charge on each capacitor
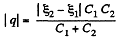
Q. 120. Determine the potential difference φA - φB between points A and B of the circuit shown in Fig. 3.23. Under what condition is it equal to zero?
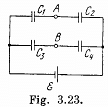
Solution. 120. Make the charge distribution, as shown in the figure. In the circuit, 12561.
-Δφ = 0 yields
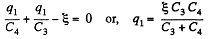
and in the circuit 13461,
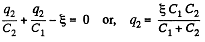
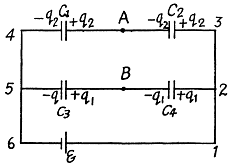
Now 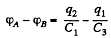
Q. 121. A capacitor of capacitance C1 = 1.0 μF charged up to a voltage V = 110 V is connected in parallel to the terminals of a circuit consisting of two uncharged capacitors connected in series and possessing the capacitances C2 = 2.0 μF and C3 = 3.0 μR. What charge will flow through the connecting wires?
Solution. 121. Let, the charge q flows through the connecting wires, then at the state of equilibrium, charge distribution will be as shown in the Fig. In the closed circuit 12341, using

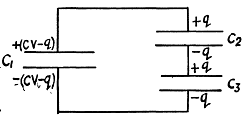
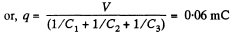
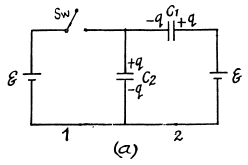
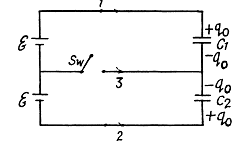
Q. 122. What charges will flow after the shorting of the switch Sw in the circuit illustrated in Fig. 3.24 through sections 1 and 2 in the directions indicated by the arrows?

Solution. 122. Initially, charge on the capacitor C1 or C2,
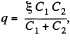 as they are in series combination (Fig.-a)
as they are in series combination (Fig.-a)
when the switch is closed, in the circuit CDEFC from - Δφ = 0, /(Fig. b)
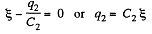 (1)
(1)
And in the closed loop BCFAB from - Δφ = 0
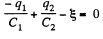 (2)
(2)
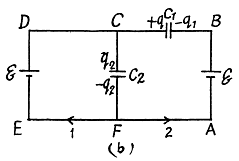
From (1) and (2) q1 - 0
Now, charge flown through section 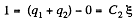
and charge flown through section 
Q. 123. In the circuit shown in Fig. 3.25 the emf of each battery is equal to  and the capacitor capacitances are equal to C1 = 2.0 μF and C2 = 3.0 μF. Find the charges which will flow after the shorting of the switch Sw through sections' 1, 2 and 3 in the directions indicated by the arrows.
and the capacitor capacitances are equal to C1 = 2.0 μF and C2 = 3.0 μF. Find the charges which will flow after the shorting of the switch Sw through sections' 1, 2 and 3 in the directions indicated by the arrows.
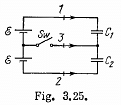
Solution. 123. When the switch is open, (Fig-a)
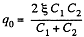
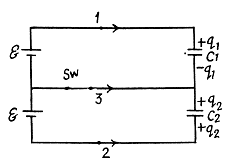
and when the switch is closed,
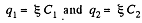
Hence, the flow of charge, due to the shortening of switch,
through section 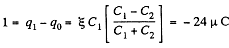
through the section 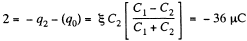
and through the section 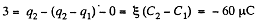
Q. 124. Find the potential difference φA — φB between points A and B of the circuit shown in Fig. 3.26.
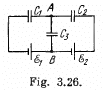
Solution. 124. First of all, make the charge distribution, as shown in the figure.
In the loop 12341, using - Δφ = 0
 (1)
(1)
Similarly, in the loop 61456, using - Δφ = 0
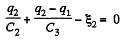 (2)
(2)
From Eqs. (1) and (2) we have
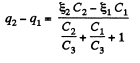
Hence, 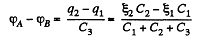
Q. 125. Determine the potential at point 1 of the circuit shown in Fig. 3.27, assuming the potential at the point O to be equal to zero. Using the symmetry of the formula obtained, write the expressions for the potentials. at points 2 and 3.
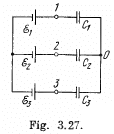
Solution. 125. In the loop ABDEA, using - Δφ = 0
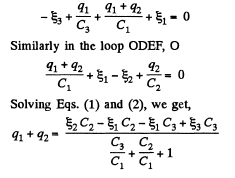
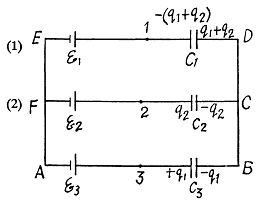
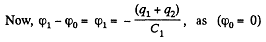
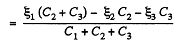
And using the symmetry 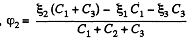
and 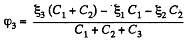
The answers have wrong sign in the book.
Q. 126. Find the capacitance of the circuit shown in Fig. 3.28 between points A and B.
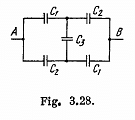
Solution. 126. Taking the advantage of symmetry of the problem charge distribution may be made, as shown in the figure.
In the loop, 12561, - Δφ = 0
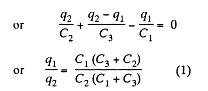

Now, capacitance of the network,
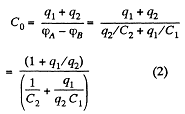
From Eqs. (1) and (2)
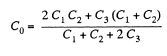
Q. 127. Determine the interaction energy of the point charges located at the corners of a square with the side a in the circuits shown in Fig. 3.29.
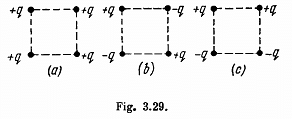
Solution. 127. (a) Interaction energy of any two point charges q1 and q2 is given by 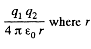 is the separation between the charges.
is the separation between the charges.
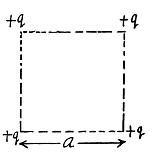
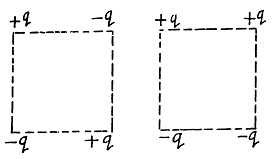
Hence, interaction energy of the system,
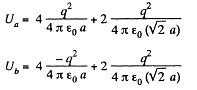
and 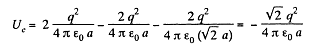
Q. 128. There is an infinite straight chain of alternating charges q and -q. The distance between the neighbouring charges is equal to a. Find the interaction energy of each charge with all the others.
Instruction. Make use of the expansion of In (1 + α) in a power series in α.
Solution. 128. As the chain is of infinite length any two charge of same sign will occur symmetrically to any other charge of opposite sign.
So, interaction energy of each charge with all the others,
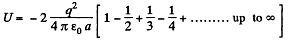 (1)
(1)
But 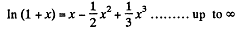
and putting 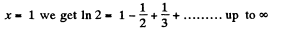 (2)
(2)
From Eqs. (1) and (2),
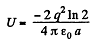
Q. 129. A point charge q is located at a distance l from an infinite tonducting plane. Find the interaction energy of that charge with chose induced on the plane.
Solution. 129. Using electrical im age method, interaction energy of the charge q with those induced on the plane.
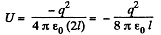
Q. 130. Calculate the interaction energy of two balls whose charges qi and q, are spherically symmetrical. The distance between the centres of the balls is equal to l.
Instruction. Start with finding the interaction energy of a ball and a thin spherical layer.
Solution. 130. Consider the interaction energy of one of the balls (say 1) and thin spherical shell of the other. This interaction energy can be written as 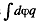
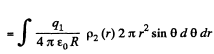
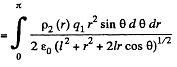
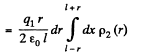
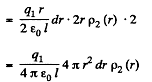
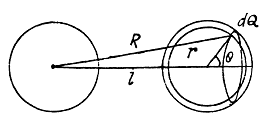
Hence finally integrating

Q. 131. A capacitor of capacitance C1 = 1.0 μF carrying initially a voltage V = 300 V is connected in parallel with an uncharged capacitor of capacitance C2 = 2.0 μF. Find the increment of the electric energy of this system by the moment equilibrium is reached. Explain the result obtained.
Solution. 131. Charge contained in the capacitor of capacitance C1 is q = C1 φ and the energy, stored in it :
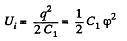
Now, when the capacitors are connected in parallel, equivalent capacitance of the system, 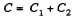 and hence, energy stored in the system :
and hence, energy stored in the system :
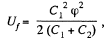 as charge remains conserved during the process.
as charge remains conserved during the process.
So, increment in the energy,
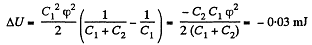
FAQs on Irodov Solutions: Electric Capacitance Energy of an Electric Field - 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is electric capacitance and how is it related to energy of an electric field? |  |
| 2. How can the energy of an electric field be calculated using capacitance? |  |
| 3. What factors affect the capacitance of an object? |  |
| 4. How does the energy stored in an electric field change when the capacitance is increased? |  |
| 5. Can the energy of an electric field be negative? |  |

|
Explore Courses for JEE exam
|

|

















