Irodov Solutions: Electric Capacitance Energy of an Electric Field - 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 132. What amount of heat will be generated in the circuit shown in Fig. 3.30 after the switch Sw is shifted from position 1 to position 2?

Solution. 132. The charge on the condensers in position 1 are as shown. Here
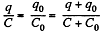
and 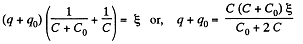
Hence, 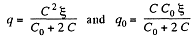

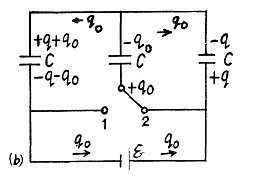
After the switch is thrown to position 2, the charges change as shown in (Fig-b).
A charge q0 has flown in the right loop through the two condensers and a charge q0 through the cell, Because of the symmetry of the problem there is no change in the energy stored in the condensers. Thus
H (Heat produced) = Energy delivered by the cell
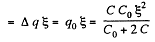
Q. 133. What amount of heat will be generated in the circuit shown. in Fig. 3.31 after the switch Sw is shifted from position 1 to position 2?
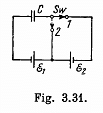
Solution. 133. Initially, the charge on the right plate of^the capacitor, 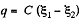 and finally, when switched to the position, 2. charge on the same plate of capacitor ;
and finally, when switched to the position, 2. charge on the same plate of capacitor ;
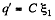
So, 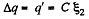
Now, from eneigy conservation,
ΔU + Heat liberated = Acell where ΔU is the electrical energy.

as only the cell with e.m.f. 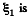 is responsible for redistribution of the charge. So,
is responsible for redistribution of the charge. So,
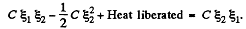
Hence heat liberated 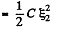
Q. 134. A system consists of two thin concentric metal shells of radii R1 and R2 with corresponding charges q1 and q2. Find the selfenergy values W1 and W2 of each shell, the interaction energy of the shells W12, and the total electric energy of the system.
Solution. 134. Self energy of each shell is given by qφ/2 where φ is the potential of the shell, created only by the charge q, on it.
Hence, self energy of the shells 1 and 2 are :
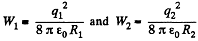
The interaction energy between the charged shells equals charge q of one shell, multiplied by the potential φ, created by other shell, at the point of location of charge q.
So, 
Hence, total enegy of the system,
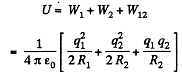
Q. 135. A charge q is distributed uniformly over the volume of a ball of radius R. Assuming the permittivity to be equal to unity, find:
(a) the electrostatic self-energy of the ball;
(b) the ratio of the energy W1 s tored in the ball to the energy W2 pervading the surrounding space.
Solution. 135. Electric fields inside and outside the sphere with the help of Gauss theorem :
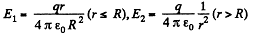
Sought self energy of the ball
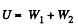
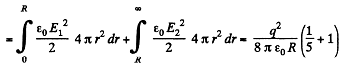
Hence,
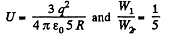
Q. 136. A point charge q = 3.0 μC is located at the centre of a spherical layer of uniform isotropic dielectric with permittivity ε = 3.0. The inside radius of the layer is equal to a = 250 mm, the outside radius is b = 500 mm. Find the electrostatic energy inside the dielectric layer.
Solution. 136. (a) By the expression 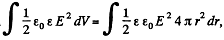 , for a spherical layer.
, for a spherical layer.
To find the electrostatic energy inside the dielectric layer, we have to integrate the upper expression in the limit [a, b] 
Q. 137. A spherical shell of radius R1 with uniform charge q is expanded to a radius R2. Find the work performed by the electric forces in this process.
Solution. 137. As the field is conservative total work done by the field force,
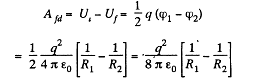
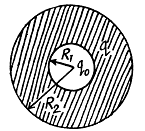
Q. 138. A spherical shell of radius R1 with a uniform charge q has a point charge q0 at its centre. Find the work performed by the electric forces during the shell expansion from radius R1 to radius R2.
Solution. 138. Initially, energy of the system, Ui = W1 + W12 where, W1 is the self energy and W12 is the mutual energy.
So, 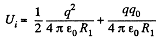
and on expansion, energy of the system,
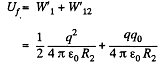
Now, work done by the field force, A equals the decrement in the electrical energy,
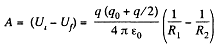
Alternate : The work of electric forces is equal to the decrease in electric energy ot the system,
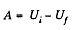
In order to find the difference 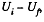 we note that upon expansion of the shell, the electric field and hence the energy localized in it, changed only in the hatched spherical layer consequently (Fig.).
we note that upon expansion of the shell, the electric field and hence the energy localized in it, changed only in the hatched spherical layer consequently (Fig.).
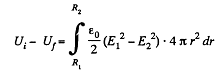
where E1 and E2 are the field intensities (in the hatched region at a distance r from the centre of the system) before and after the expansion of the shell. By using Gauss’ theorem, we find
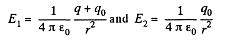
As a result of integration, we obtain

Q. 139. A spherical shell is uniformly charged with the surface derisity σ. Using the energy conservation law, find the magnitude of the electric force acting on a unit area of the shell.
Solution. 139. Energy of the charged sphere of radius r, from the equation
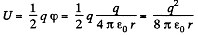
If the radius of the shell changes by dr then work done is
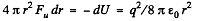
Thus sought force per unit area,
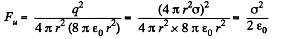
Q. 140. A point charge q is located at the centre O of a spherical uncharged conducting layer provided with a small orifice (Fig. 3.32). The inside and outside radii of the layer are equal to a and b respectively. What amount of work has to be performed to slowly transfer the charge q from the point O through the orifice and into infinity?
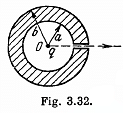
Solution. 140. Initially, there will be induced charges of magnitude - q and +q on the inner and outer surface of the spherical layer respectively. Hence, the total electrical energy of the system is the sum of self energies of spherical shells, having radii a and b, and their mutual energies including the point charge q.
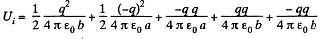
or 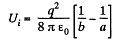
Finally, charge q is at infinity hence, Uf = 0
Now, work done by the agent = increment in the energy
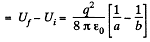
Q. 141. Each plate of a parallel-plate air capacitor has an area S. What amount of work has to be performed to slowly increase the distance between the plates from x1 to x2 if
(a) the capacitance of the capacitor, which is equal to q, or
(b) the voltage across the capacitor, which is equal to V, is kept constant in the process?
Solution. 141. (a) Sought work is equivalent to the work performed against the electric field created by one plate, holding at rest and to bring the other plate away. Therefore the required work,
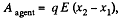
where 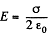 is the intensity of the field created by one plate at the location of other.
is the intensity of the field created by one plate at the location of other.
So, 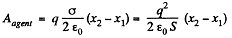
Alternate :  (as field is potential)
(as field is potential)
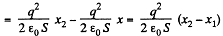
(b) When voltage is kept const., the force acing on each plate of capacitor will depend on the distance between the plates.
So, elementary work done by agent, in its displacement over a distance dx, relative to the other,
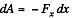
But, 
Hence, 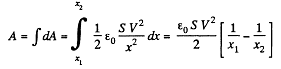
Alternate : From energy Conservation,
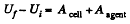
or 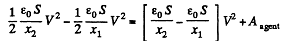
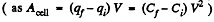
So 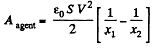
Q. 142. Inside a parallel-plate capacitor there is a plate parallel to the outer plates, whose thickness is equal to η = 0.60 of the gap width. When the plate is absent the capacitor capacitance equals c = 20 nF. First, the capacitor was connected in parallel to a constant voltage source producing V = 200 V, then it was disconnected from it, after which the plate was slowly removed from the gap. Find the work performed during the removal, if the plate is
(a) made of metal; (b) made of glass.
Solution. 142. (a) When metal plate of thickness ηd is inserted inside the capacitor, capacitance of the system becomes 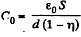
Now, initially, charge on the capacitor, 
Finally, capacitance of the capacitor, 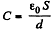
As the source is disconnected, charge on the plates will remain same during the process.
Now, from energy conservation,
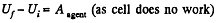
or, 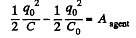
Hence 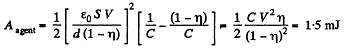
(b) Initially, capacitance of the system is given by,
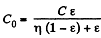 this is the cap acitance of two capacitors in series)
this is the cap acitance of two capacitors in series)
So, charge on the plate, 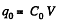
Capacitance of the capacitor, after the glass plate has been removed equals C
From energy conservation,

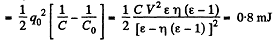
Q. 143. A parallel-plate capacitor was lowered into water in a horizontal position, with water filling up the gap between the plates d = 1.0 mm wide. Then a constant voltage V = 500 V was applied to the capacitor. Find the water pressure increment in the gap.
Solution. 143. When the capactior which is immersed in water is connected to a constant voltage source, it gets charged. Suppose σ0 is the free charge density on the condenser plates. Because water is a dielectric, bound charges also appear in it Let σ' be the surface density of bound charges. (Because of homogeneity of the medium and uniformity of the field when we ignore edge effects no volume density of bound charges exists.) The electric field due to free charges only 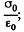 that due to bound charges is
that due to bound charges is 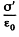 and the total electric field is
and the total electric field is 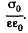 Recalling that the sign of bound charges is opposite o f the free charges, we have
Recalling that the sign of bound charges is opposite o f the free charges, we have
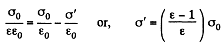
Because of the field that exists due to the free charges (not the total field; the field due to the bound charges must be excluded for this purpose as they only give rise to self energy effects), there is a force attracting the bound charges to the near by plates. This force is
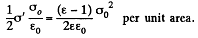
The factor 1/2 needs an explanation. Normally the force on a test charge is qE in an electric field E. But if the chaige itself is produced by the electric filed then the force must be constructed bit by bit and is
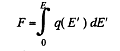
if 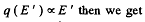
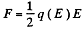
This factor of 1/2 is well known. For exaipple the energy of a dipole of moment 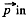 in an electric field
in an electric field 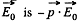 while the energy per unit volume o f a linear dielectric in an electric field is
while the energy per unit volume o f a linear dielectric in an electric field is 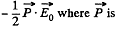 the polarization vector (i.e. dipole moment per unit volume). Now the force per unit area manifests ifself as excess pressure of the liquid.
the polarization vector (i.e. dipole moment per unit volume). Now the force per unit area manifests ifself as excess pressure of the liquid.
Noting that 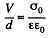
We get 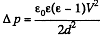
Substitution, using ε = 81 for water, gives Δp = 7.17 k Pa = 0.07 atm.
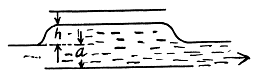
Q. 144. A parallel-plate capacitor is located horizontally so that one of its plates is submerged into liquid while the other is over its surface (Fig. 3.33). The permittivity of the liquid is equal to ε, its density is equal to p. To what height will the level of the liquid in the capacitor rise after its plates get a charge of surface density σ?
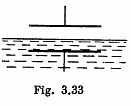
Solution. 144. One way of doing this problem will be exactly as in the previous case so let us try an alternative method based on energy. Suppose the liquid rises by a distance h. Then let us calculate the extra energy of the liquid as a sum of polarization energy and the ordinary gravitiational energy. The latter is
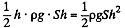
If σ is the free charge surface density on the plate, the bound charge density is, from the previous problem,
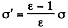
This is also the volume density of induced dipole moment i.e. Polarization. Then the energy is, as before

and the total polarization energy is
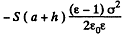
Then, total eneigy is

The actual height to which the liquid rises is determined from the formula
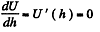
This gives 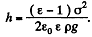
Q. 145. A cylindrical layer of dielectric with permittivity ε is inserted into a cylindrical capacitor to fill up all the space between the electrodes. The mean radius of the electrodes equals R, the gap between them is equal to d, with d ≪ R. The constant voltage V is applied across the electrodes of the capacitor. Find the magnitude of the electric force pulling the dielectric into the capacitor.
Solution. 145. We know that energy of a capacitor 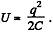
Hence,  (1)
(1)
Now, since d << R, the capacitance of the given capacitor can be calculated by the formula of a parallel plate capacitor. Therefore, if the dielectric is introduced upto a depth x and the length of the capacitor is l, we have,
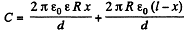 (2)
(2)
From (1) and (2), we get,
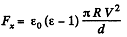
Q. 146. A capacitor consists of two stationary plates shaped as a semi-circle of radius R and a movable plate made of dielectric with permittivity a and capable of rotating about an axis O between the stationary plates (Fig. 3.34). The thickness of the movable plate is equal to d which is practically the separation between the stationary plates. A potential difference V is applied to the capacitor. Find the magnitude of the moment of forces relative to the axis O acting on the movable plate in the position shown in the figure.

Solution. 146. When the capacitor is kept at a constant potential difference V, the work performed by the moment of electrostatic forces between the plates when the inner moveable plate is rotated by an angle dφ equals the increase in the potential energy of the system. This comes about because when charges are made, charges flow from the battery to keep the potential constant and the amount of the work done by these charges is twice in magnitude and opposite in sign to the change in the energy of the capacitor Thus 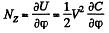
Now the capacitor can be thought of as made up two parts (with and without the dielectric) in parallel.
Thus 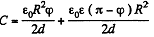
as the area of a sector of angle 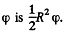 Differentiation then gives
Differentiation then gives
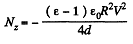
The negative sign of Nz indicates that the moment of the force is acting clockwise (i.e. trying to suck in the dielectric).
FAQs on Irodov Solutions: Electric Capacitance Energy of an Electric Field - 3 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the definition of electric capacitance? |  |
| 2. How is the energy of an electric field related to capacitance? |  |
| 3. How can the electric field energy be calculated for a given capacitor? |  |
| 4. What factors affect the energy stored in an electric field? |  |
| 5. How is the energy of an electric field related to the work done in charging a capacitor? |  |


















