Irodov Solutions: Electric Current - 4 - Airforce X Y / Indian Navy SSR PDF Download
Q. 201. A glass plate totally fills up the gap between the electrodes of a parallel-plate capacitor whose capacitance in the absence of that glass plate is equal to C = 20 nF. The capacitor is connected to a do voltage source V = 100 V. The plate is slowly, and without friction, extracted from the gap. Find the capacitor energy increment and the mechanical work performed in the process of plate extraction.
Solution. 201. Initially, capacitance of the system = C ε
So, initial energy of the system : 
and finally, energy of the capacitor : 
Hence capacitance energy increment,
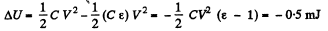
From energy conservation
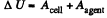
(as there is no heat liberation)
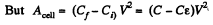
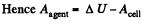
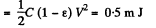
Q. 202. A cylindrical capacitor connected to a de voltage source V touches the surface of water with its end (Fig. 3.56). The separation d between the capacitor electrodes is substantially less than their mean radius. Find a height h to which the water level in the gap will rise. The capillary effects are to be neglected.
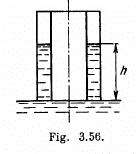
Solution. 202. If C0 is the initial capacitance of the condenser before water rises in it then

(R is the mean radius and / is the length of the capacitor plates.)
Suppose the liquid rises to a height h in it. Then the capacitance of the condenser is
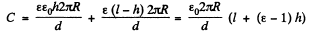
and energy of the capacitor and the liquid (including both gravitational and electrosatic contributions) is
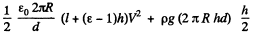
If the capacitor were not connected to a battery this energy would have to be minimized.
But the capacitor is connected to the battery and, in effect, the potential energy of the whole system has to be minimized. Suppose we increase h by bh. Then the energy of the capacitor and the liquid increases by
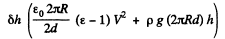
and that of the cell diminishes by the quantity Acell which is the p rod uct o f charge flown and V

In equilibrium, the two must balance; so
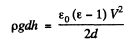
Hence 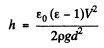
Q. 203. The radii of spherical capacitor electrodes are equal to a and b, with a < b. The interelectrode space is filled with homogeneous substance of permittivity ε and resistivity p. Initially the capacitor is not charged. At the moment t = 0 the internal electrode gets a charge q0. Find:
(a) the time variation of the charge on the internal electrode;
(b) the amount of heat generated during the spreading of the charge.
Solution. 203. (a) Let us mentally islolate a thin spherical layer with inner and outer radii r and r + dr respectively. Lines of current at all the points of this layer are perpendicular to it and therefore such a layer can be treated as a spherical conductor of thickness dr and cross sectional area 4 πr2 . Now, we know that resistance,
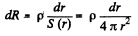 (1)
(1)
Integrating expression (1) between the limits,
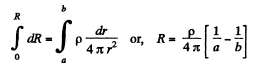 (2)
(2)
Capacitance of the network, 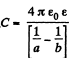 (3)
(3)
and 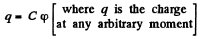 (4)
(4)
also, 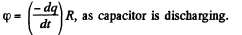 (5)
(5)
From Eqs. (2), (3), (4) and (5) we get,

Integrating 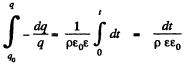
Hence 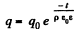
(b) From energy conservation heat generated, during the spreading of the charge,
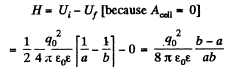
Q. 204. The electrodes of a capacitor of capacitance C = 2.00 μF carry opposite charges q0 = 1.00 mC. Then the electrodes are interconnected through a resistance R = 5.0 MΩ. Find:
(a) the charge flowing through that resistance during a time interval τ = 2.00 s;
(b) the amount of heat generated in the resistance during the same interval.
Solution. 204. (a) Let, at any moment of time, charge on the plates be (q0 - q) then current through the resistor, 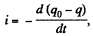 because the capacitor is discharging.
because the capacitor is discharging.
or, 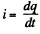
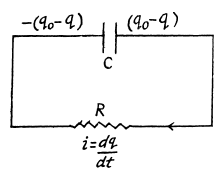
Now, applying loop rule in the circuit,
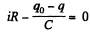
or, 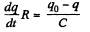
or, 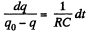
At t = 0, q = 0 and at t = τ, q = q
So, 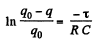
Thus 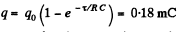
(b) Amount of heat generated = decrement in capacitance energy
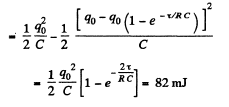
Q. 205. In a circuit shown in Fig. 3.57 the capacitance of each capacitor is equal to C and the resistance, to R. One of the capacitors was connected to a voltage V0 and then at the moment t = 0 was shorted by means of the switch Sw. Find:
(a) a current I in the circuit as a function of time t;
(b) the amount of generated heat provided a dependence I (t) is known.
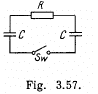
Solution. 205. Let, at any moment of time, charge flown be q then current 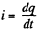
Applying loop rule in the circuit, 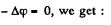

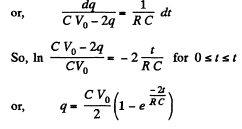
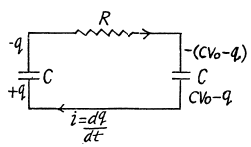
Hence, 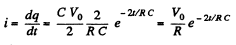
Now, heat liberaled,
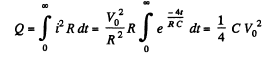
Q. 206. A coil of radius r = 25 cm wound of a thin copper wire of length l = 500 m rotates with an angular velocity ω = 300 rad/s about its axis. The coil is connected to a ballistic galvanometer by means of sliding contacts. The total resistance of the circuit is equal to R = 21 Ω. Find the specific charge of current carriers in copper if a sudden stoppage of the coil makes a charge q = 10 nC flow through the galvanometer.
Solution. 206. in a rotating frame, to first order in ω, the main effect is a coriolis force 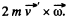 This unbalanced force will cause electrons to react by setting up a magnetic field
This unbalanced force will cause electrons to react by setting up a magnetic field 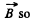 that the magnetic force
that the magnetic force 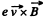 balances the coriolis force.
balances the coriolis force.
Thus 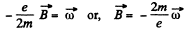
The flux associated with this is

where 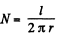 is the number of turns of the ring. If ω changes (and there is time for the electron to rearrange) then B also changes and so
is the number of turns of the ring. If ω changes (and there is time for the electron to rearrange) then B also changes and so 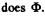 An emf will be induced and a current will flow. This is
An emf will be induced and a current will flow. This is

The total charge flowing through the ballastic galvanometer, as the ring is stopped, is
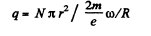
So, 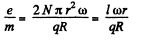
Q. 207. Find the total momentum of electrons in a straight wire of length l = 1000 m carrying a current I = 70 A.
Solution. 207. Let, n0 be the total number of electoms then, total momentum of electoms,
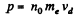 (1)
(1)
Now, 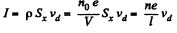
Here Sx = Cross sectional area, p = electron charge density, V = volume of sample From (1) and (2)
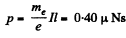
Q. 208. A copper wire carries a current of density j = 1.0 A/mm2. Assuming that one free electron corresponds to each copper atom, evaluate the distance which will be covered by an electron during its displacement l = 10 mm along the wire.
Solution. 208. By definition
ne vd = j (where vd is drift velocity, n is number density of electrons.)
Then 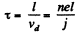
So distance actually travelled
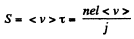
(<v> = mean velocity of thermal motion of an electron)
Q. 209. A straight copper wire of length l = 1000 m and crosssectional area S = 1.0 mm2 carries a current I = 4.5 A. Assuming that one free electron corresponds to each copper atom, find:
(a) the time it takes an electron to displace from one end of the wire to the other;
(b) the sum of electric forces acting on all free electrons in the given wire.
Solution. 209. Let, n be the volume density of electrons, then from 
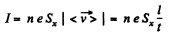
So, 
(b) Sum of electric forces
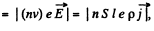 where p is resistivity of die material.
where p is resistivity of die material.

Q. 210. A homogeneous proton beam accelerated by a potential difference V = 600 kV has a round cross-section of radius r = 5.0 mm. Find the electric field strength on the surface of the beam and the potential difference between the surface and the axis of the beam if the beam current is equal to I = 50 mA.
Solution. 210. From Gauss theorem field strength at a surface of a cylindrical shape equals, 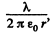 where X is the linear chaige density.
where X is the linear chaige density.
Now, 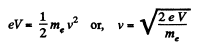
Also, 
or, 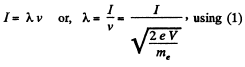
Hence 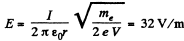
(b) For the point, inside the solid charged cylinder, applying Gauss’ theorem,
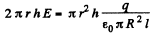
or, 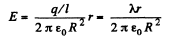
So,from 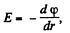
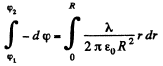
or, 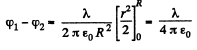
Hence, 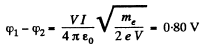
Q. 211. Two large parallel plates are located in vacuum. One of them serves as a cathode, a source of electrons whose initial velocity is negligible. An electron flow directed toward the opposite plate produces a space charge causing the potential in the gap between the plates to vary as φ = ax4/3, where a is a positive constant, and x is the distance from the cathode. Find:
(a) the volume density of the space charge as a function of x;
(b) the current density.
Solution. 211. Between the plates 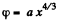
or, 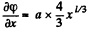
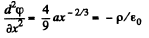
or, 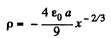
Let the charge on the electron be - e,
then 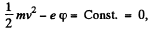
as the electron is initially emitted with neligible energy.
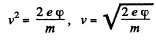
So, 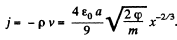
(j is measued from the anode to cathode, so the - ve sign.)
Q. 212. The air between two parallel plates separated by a distance d = 20 mm is ionized by X-ray radiation. Each plate has an area S = 500 cm2. Find the concentration of positive ions if at a voltage V = 100 V a current I = 3.0 μ,A flows between the plates, which is well below the saturation current. The air ion mobilities are 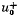 = 1.37 cm2/(V•s) and
= 1.37 cm2/(V•s) and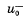 = 1.91 cm2/(V•s).
= 1.91 cm2/(V•s).
Solution. 212.
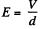
So by the definition of the mobility
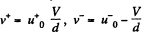
and 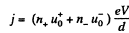
(The negative ions move towards the anode and the positive ion towards the cathode and the total current is the sum of the currents due to them.) On the other hand, in equilibrium n+ = n_
So, 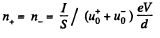
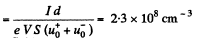
Q. 213. A gas is ionized in the immediate vicinity of the surface of plane electrode l (Fig. 3.58) separated from electrode 2 by a distance l. An alternating voltage varying with time t as V = V0 sin cot is applied to the electrodes. On decreasing the frequency ω it was observed that the galvano- meter G indicates a current only at ω < ω0 where ω0 is a certain cut-off frequency. Find the mobility of ions reaching electrode 2 under these conditions.
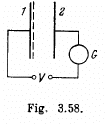
Solution. 213. Velocity = mobility x field
 which is positive for 0 < ω t < π
which is positive for 0 < ω t < π
So, maximum displacement in one direction is
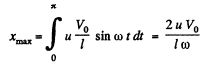
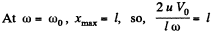
Thus 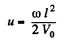
Q. 214. The air between two closely located plates is uniformly ionized by ultraviolet radiation. The air volume between the plates is equal to V = 500 cm3, the observed saturation current is equal to Isat = 0.48 μA. Find :
(a) the number of ion pairs produced in a unit volume per unit time;
(b) the equilibrium concentration of ion pairs if the recombination coefficient for air ions is equal to r = 1.67.10-6 cm3/s.
Solution. 214. When the current is saturated, all the ions, produced, reach the plate.
Then, 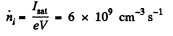
(Both positive ions and negative ions are counted here)
The equation of balance is 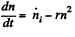
The first term on the right is the production rate and the second term is the recombination rate which by the usual statistical arguments is proportional to n2 (= no of positive ions x no. of -ve ion). In eauilibrium.
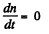
so, 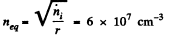
Q. 215. Having been operated long enough, the ionizer producing ni = 3.5.109 cm-3 •s -1 of ion pairs per unit volume of air per unit time was switched off. Assuming that the only process tending to reduce the number of ions in air is their recombination with coefficient r = 1.67.10-6 cm3/s, find how soon after the ionizer's switching off the ion concentration decreases η= 2.0 times.
Solution. 215. Initially 
Since we can assume that the long exposure to the ionizer has caused equilibrium to be set up. Afer the ionizer is switched off,
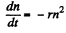
or 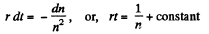
But 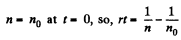
The concentration will decrease by a factor η when
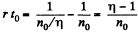
or, 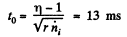
Q. 216. A parallel-plate air capacitor whose plates are separated by a distance d = 5.0 mm is first -charged to a potential difference V = 90 V and then disconnected from a de voltage source. Find the time interval during which the voltage across the capacitor decreases by η = 1.0%, taking into account that the average number of ion pairs formed in air under standard conditions per unit volume per unit time is equal to ni = 5.0 cm-3 •s-1 and that the given voltage corresponds to the saturation current.
Solution. 216. Ions produced will cause charge to decay. Clearly,
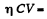 decrease of charge
decrease of charge 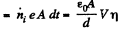
or, 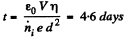
Note , that ni, here, is the number of ion pairs produced.
Q. 217. The gap between two plane plates of a capacitor equal to d is filled with a gas. One of the plates emits v0 electrons per second which, moving in an electric field, ionize gas molecules; this way each electron produces α new electrons (and ions) along a unit length of its path. Find the electronic current at the opposite plate, neglecting the ionization of gas molecules by formed ions.
Solution. 217. If v = number of electrons moving to the anode at distance x, then
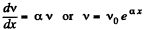
Assuming saturation, 
Q. 218. The gas between the capacitor plates separated by a dist- ance d is uniformly ionized by ultraviolet radiation so that ni electrons per unit volume per second are formed. These electrons moving in the electric field of the capacitor ionize gas molecules, each electron producing α new electrons (and ions) per unit length of its path. Neglecting the ionization by ions, find the electronic current density at the plate possessing a higher potential.
Solution. 218. Since the electrons are produced uniformly through the volume, the total current attaining saturation is clearly,
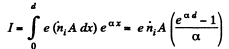
Thus, 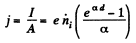
FAQs on Irodov Solutions: Electric Current - 4 - Airforce X Y / Indian Navy SSR
| 1. What is electric current and how is it measured? |  |
| 2. What is Ohm's law and how is it related to electric current? |  |
| 3. What is the difference between direct current (DC) and alternating current (AC)? |  |
| 4. How does resistance affect the flow of electric current? |  |
| 5. What are the factors that affect the resistance of a conductor? |  |














