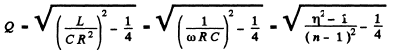Irodov Solutions: Electric Oscillations- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.111. An oscillating circuit incorporates a leaking capacitor. Its capacitance is equal to C and active resistance to R. The coil inductance is L. The resistance of the coil and the wires is negligible. Find:
(a) the damped oscillation frequency of such a circuit;
(b) its quality factor.
Ans. In a leaky condenser
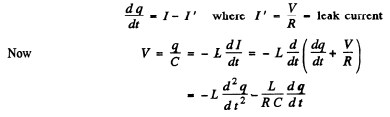
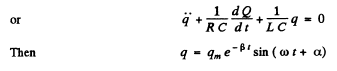
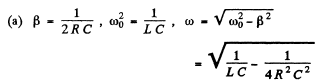
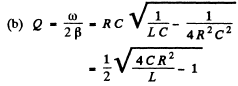
Q.112. Find the quality factor of a circuit with capacitance C = = 2.0 μF and inductance L = 5.0 mH if the maintenance of undamped oscillations in the circuit with the voltage amplitude across the capacitor being equal to Vm = 1.0 V requires a power (P) 0.10 mW. The damping of oscillations is sufficiently low.
Ans.
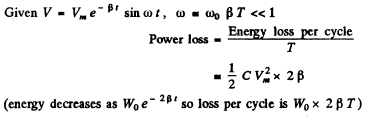
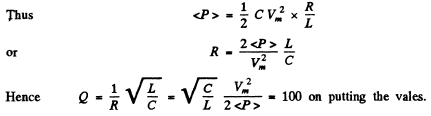
Q.113. What mean power should be fed to an oscillating circuit with active resistance R = 0.45Ω to maintain undamped harmonic oscillations with current amplitude Im = 30 mA?
Ans. Energy is lost across the resistance and the mean power lass is
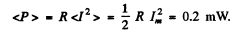
This power should be fed to the circuit to maintain undamped oscillations.
Q.114. An oscillating circuit consists of a capacitor with capacitance C = 1.2 nF and a coil with inductance L = 6.0 iLtli and active resistance R = 0.50Ω. What mean power should be fed to the circuit to maintain undamped harmonic oscillations with voltage amplitude across the capacitor being equal to Vm = 10 V?
Ans. 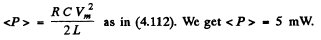
Q.115. Find the damped oscillation frequency of the circuit shown in Fig. 4.30. The capacitance C, inductance L, and active resistance R are supposed to be known. Find how must C, L, and R be interrelated to make oscillations possible.
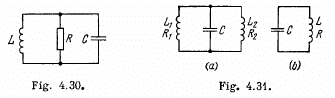
Ans.
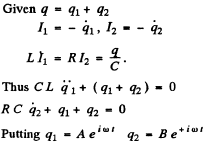
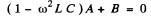
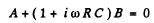
A solution exists only if
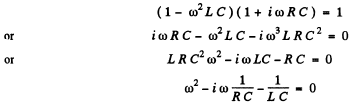
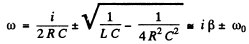
Thus 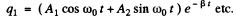
ω0 is the oscillation frequency. Oscillations are possible only if 
i.e. 
Q.116. There are two oscillating circuits (Fig. 4.31) with capacitors of equal capacitances. How must inductances and active resistances of the coils be interrelated for the frequencies and damping of free oscillations in both circuits to be equal? The mutual inductance of coils in the left circuit is negligible.
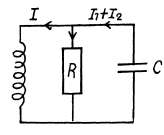
Ans. We have
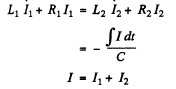
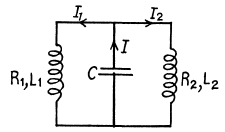
Then differentiating we have the equations
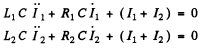
Look for a solution
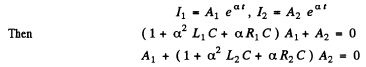
This set of simultaneous equations has a nontrivial solution only if

This cubic equation has one real root which we ignore and two complex conjugate roots. We require the condition that this pair of complex conjugate roots is identical with the roots of the equation
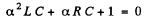
The general solution of this problem is not easy.We look for special cases. If R1 = R2 = 0, thei
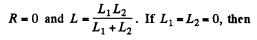
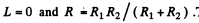 These are the quoted solution but they are misleading.
These are the quoted solution but they are misleading.
We shall give the solution for small R1, R2 . Then we put 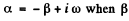 is small
is small
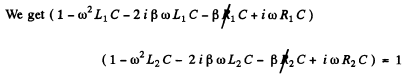
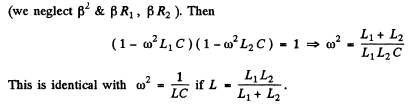
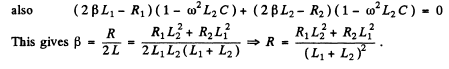
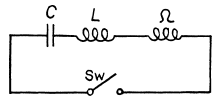
Q.117. A circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch
disconnected, the capacitor was charged to a voltage Vo, and at the moment t = 0 the switch was closed. Find the current I in the circuit as a function of time t. What is Imax equal to?
Ans.
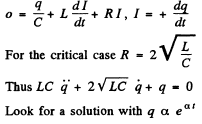
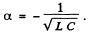
An independent solution is 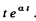 Thus
Thus
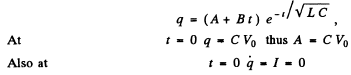
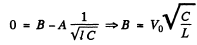
Thus filially
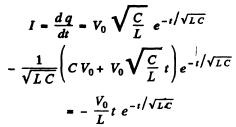
The current has been defined to increase the charge. Hence the minus sign.
The current is maximum when
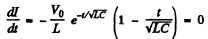
This gives 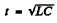 and the magnitude of the maximum current is
and the magnitude of the maximum current is
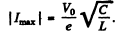
Q.118. A coil with active resistance R and inductance L was connected at the moment t = 0 to a source of voltage V = Vm cos ωt. Find the current in the coil as a function of time t.
Ans. The equation o f the circuit is ( I is th e current)
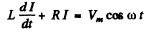
From the theory of differential equations
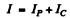
where IP is a particular integral and IC is the complementary function (Solution of the differential equation with the RHS = 0 ). Now
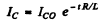
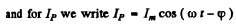
Substituting we get
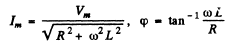
Thus 
Now in an inductive circuit I = 0 at t = 0
because a current cannot change suddenly.
Thus 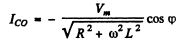
and so
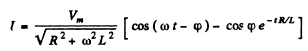
Q.119. A circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t = 0 to a source of ac voltage V = Vm cos ωt. Find the current in the circuit as a function of time t.
Ans. Here the equation is (Q is charge on the capacitor)
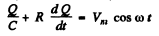
A solution subject to Q = 0 at t = 0 is of the form (as in the previous problem)
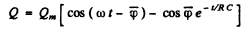
Substituting back
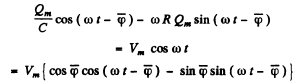
so
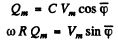
This leads to
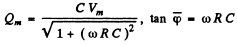
Hence
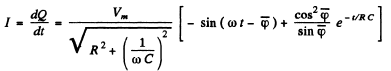
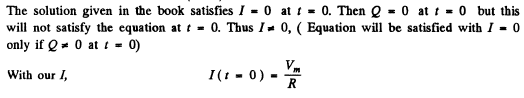
Q.120. A long one-layer solenoid tightly wound of wire with resistivity p has n turns per unit length. The thickness of the wire insulation is negligible. The cross-sectional radius of the solenoid is equal to a. Find the phase difference between current and alternating voltage fed to the solenoid with frequency v.
Ans. The current lags behind the voltage by the phase angle
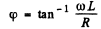
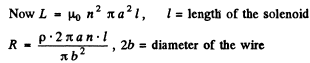
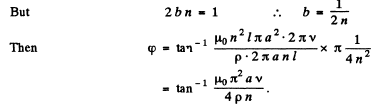
Q.121. A circuit consisting of a capacitor and an active resistance R = 110Ω connected in series is fed an alternating voltage with amplitude Vm = 110 V. In this case the amplitude of steady-state current is equal to Im = 0.50 A. Find the phase difference between the current and the voltage fed.
Ans.
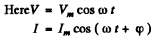
where

Now
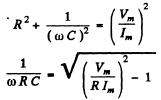
Thus the current is ahead of the voltage by
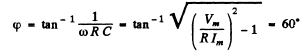
Q.122. Fig. 4.32 illustrates the simplest ripple filter. A voltage V = V0 (1. + cos ωt) is fed to the left input. Find: (a) the output voltage V' (t); (b) the magnitude of the product RC at which the output amplitude of alternating voltage component is η = 7.0 times less than the direct voltage component, if ω = 314 s-1.
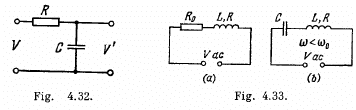
Ans.
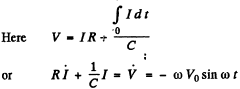
Ignoring transients, a solution has the form
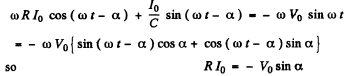
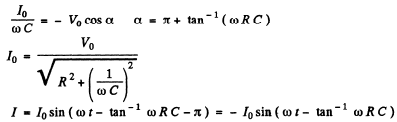
Then 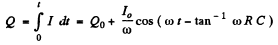
It satisfies 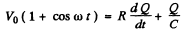
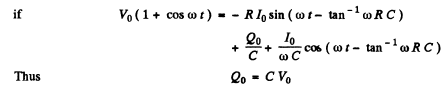
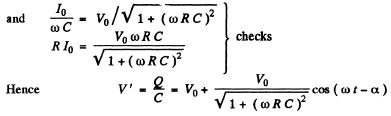
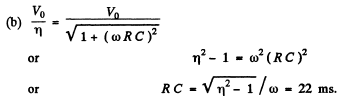
Q.123. Draw the approximate voltage vector diagrams in the electric circuits shown in Fig. 4.33 a, b. The external voltage V is assumed to be alternating harmonically with frequency ω.
Ans.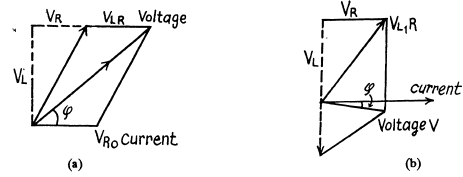
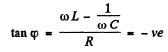
as 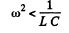
Q.124. A series circuit consisting of a capacitor with capacitance C = 22 μF and a coil with active resistance R = 20Ω and inductance L = 0.35 H is connected to a source of alternating voltage with amplitude Vm = 180 V and frequency ω = 314 s-1. Find:
(a) the current amplitude in the circuit;
(b) the phase difference between the current and the external voltage;
(c) the amplitudes of voltage across the capacitor and the coil.
Ans. (a)
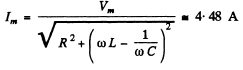
(b)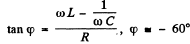
Current lags behind the voltage 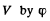
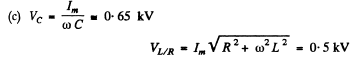
Q.125. A series circuit consisting of a capacitor with capacitance C, a resistance R, and a coil with inductance L and negligible active resistance is connected to an oscillator whose frequency can be varied without changing the voltage amplitude. Find the frequency at which the voltage amplitude is maximum
(a) across the capacitor;
(b) across the coil.
Ans. (a)
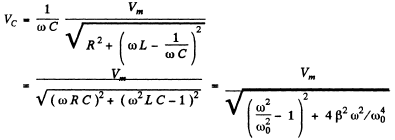

This is maximum when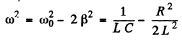
(b)
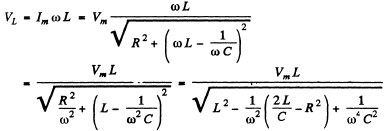
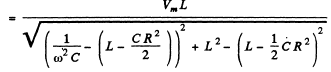
This is maximum when
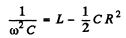
or
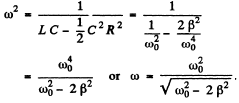
Q.126. An alternating voltage with frequency ω = 314s-1 and amplitude Vm = 180 V is fed to a series circuit consisting of a capacitor and a coil with active resistance R = 40Ω and inductance L = 0.36 H. At what value of the capacitor's capacitance will the voltage amplitude across the coil be maximum? What is this amplitude equal to? What is the corresponding voltage amplitude across the condenser?
Ans.
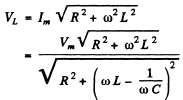
for a given ω , L , R , this is maximum when
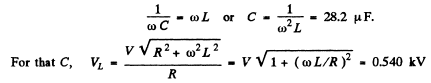
At this C, 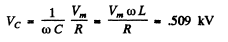
Q.127. A capacitor with capacitance C whose interelectrode space is filled up with poorly conducting medium with active resistance R is connected to a source of alternating voltage V = Vm cos ωt. Find the time dependence of the steady-state current flowing in lead wires. The resistance of the wires is to be neglected.
Ans.
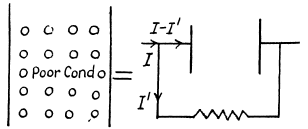
We use the complex voltage 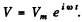 Then the voltage across the capacitor is
Then the voltage across the capacitor is
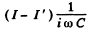
and that across the resistance R I ' and both equal V . Thus
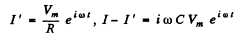
Hence
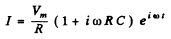
The actual voltage is obtained by taking the real part Then
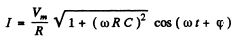
Where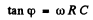
Note → A condenser with poorly conducting material (dielectric of high resistance) be the plates is equvalent to an an ideal condenser with a high resistance joined in p between its plates.
Q.128. An oscillating circuit consists of a capacitor of capacitance C and a solenoid with inductance L1. The solenoid is inductively connected with a short-circuited coil having an inductance L2 and a negligible active resistance. Their mutual inductance coefficient is equal to L12. Find the natural frequency of the given oscillating circuit.
Ans.
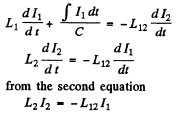

Then
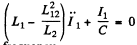
Thus the current oscillates with frequency

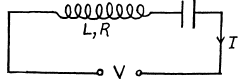
Q.129. Find the quality factor of an oscillating circuit connected in series to a source of alternating emf if at resonance the voltage across the capacitor is n times that of the source.
Ans.
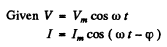
where

Then, 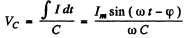
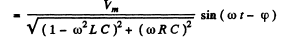
As resonance the voltage amplitude across the capacitor
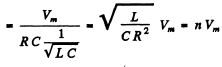
So 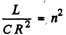
Now 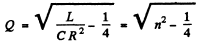
Q.130. An oscillating circuit consisting of a coil and a capacitor connected in series is fed an alternating emf, with coil inductance being chosen to provide the maximum current in the circuit. Find the quality factor of the system, provided an n-fold increase of inductance results in an ii-fold decrease of the current in the circuit.
Ans. For maximum current amplitude
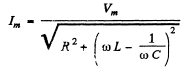
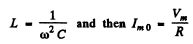
Now 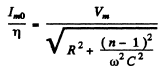
So
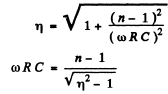
Now