Irodov Solutions: Electromagnetic Waves. Radiation- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.189. An electromagnetic wave of frequency v = 3.0 MHz passes from vacuum into a non-magnetic medium with permittivity a = 4.0. Find the increment of its wavelength.
Ans. The velocity of light in a medium of relative permittivity 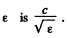 Thus the change in wavelength of light (from its value in vaccum to its value in the medium) is
Thus the change in wavelength of light (from its value in vaccum to its value in the medium) is
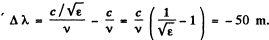
Q.190. A plane electromagnetic wave falls at right angles to the surface of a plane-parallel plate of thickness l. The plate is made of non-magnetic substance whose permittivity decreases exponentially from a value al at the front surface down to a value a, at the rear one. How long does it take a given wave phase to travel across this plate?
Ans. From the data of the problem the relative permittivity of the medium varies as
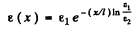
Hence the local velocity of light
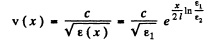
Thus the required time 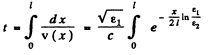
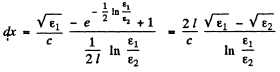
Q.191. A plane electromagnetic wave of frequency v = 10 MHz propagates in a poorly conducting medium with conductivity σ = = 10 mS/m and permittivity ε = 9. Find the ratio of amplitudes of conduction and displacement current densities.
Ans. Conduction current density 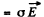
Displacement current density 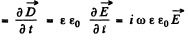
Ratio of magnitudes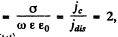 on puting the values.
on puting the values.
Q.192. A plane electromagnetic wave E = Em cos (ωt— kr) propagates in vacuum. Assuming the vectors Em and k to be known, find the vector H as a function of time t at the point with radius vector r = 0.
Ans.
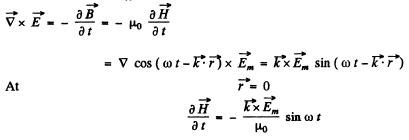
So integrating (ignoring a constant) and using 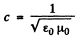
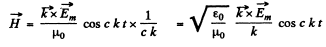
Q.193. A plane electromagnetic wave E = Em cos (ωt— kr), where Em, = Emey, k = kex, ex, eu are the unit vectors of the x, y axes, propagates in vacuum. Find the vector H at the point with radius vector r = xex at the moment (a) t = 0, (b) t = to. Consider the case when Em =1 60 V/m, k = 0.51 m-1, x = 7.7 m, and to = = 33 ns.
Ans. As in the previous problem
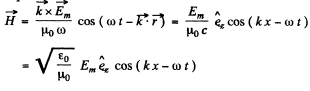
Thus
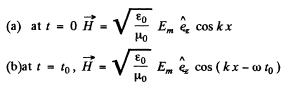
Q.194. A plane electromagnetic wave E = Em, cos (ωt— kx) propagating in vacuum induces the emf gin, in a square frame with side l. The orientation of the frame is shown in Fig. 4.37. Find the amplitude value εind, if Em = 0.50 mV/m, the frequency v =5.0 MHz and l = 50 cm.
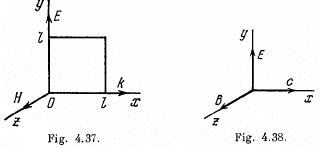
Ans.
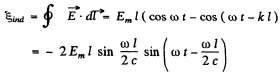
Putting the values
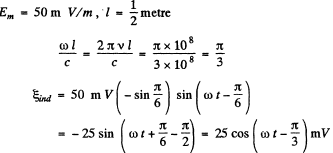
Q.195. Proceeding from Maxwell's equations show that in the case of a plane electromagnetic wave (Fig. 4.38) propagating in vacuum the following relations hold:
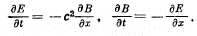
Ans.

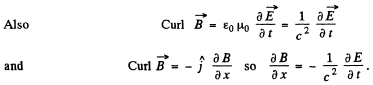
Q.196. Find the mean Poynting vector (8) of a plane electromagnetic wave E = Em cos (ωt— kr) if the wave propagates in vacuum.
Ans.
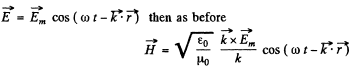
So
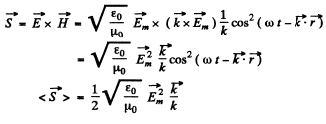
Q.197.. A plane harmonic electromagnetic wave with plane polarization propagates in vacuum. The electric component of the wave has a strength amplitude Em = 50 mV/m, the frequency is v 100 MHz. Find:
(a) the efficient value of the displacement current density;
(b) the mean energy flow density averaged over an oscillation period.
Ans.
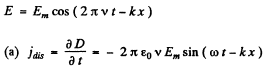
Thus
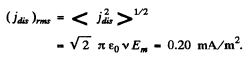
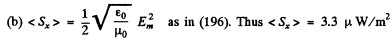
Q.198. A ball of radius R = 50 cm is located in a non-magnetic medium with permittivity ε = 4.0. In that medium a plane electromagnetic wave propagates,the strength amplitude of whose electric component is equal to Em = 200 Vim. What amount of energy reaches the ball during a time interval t = 1.0 min?
Ans. For the Poynting vector we can derive as in (196)
 along the direction of propagation.
along the direction of propagation.
Hence in time t (which is much longer than the time period T of the wave), the eneigy reaching the ball is
Q.199. A standing electromagnetic wave with electric component E = Em cos kx•cos ωt is sustained along the x axis in vacuum. Find the magnetic component of the wave B (x, t). Draw the approximate distribution pattern of the wave's electric and magnetic components (E and B) at the moments t = 0 and t = T/4, where T is the oscillation period.
Ans.
Also
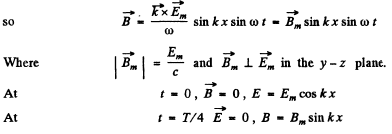
Q.200. A standing electromagnetic wave E = Em cos kx• cos ωt is sustained along the x axis in vacuum. Find the projection of the Poynting vector on the x axis sx (x, t) and the mean value of that projection averaged over an oscillation period.
Ans.
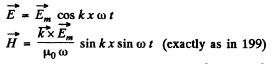
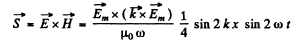
Thus
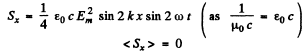
Q.201. A parallel-plate air capacitor whose electrodes are shaped as discs of radius R = 6.0 cm is connected to a source of an alternating sinusoidal voltage with frequency ω = 1000 s-1. Find the ratio of peak values of magnetic and electric energies within the capacitor.
Ans. Inside the condenser the peak electrical energy 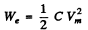
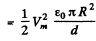
(d = separation between the plates, πR2 = area of each plate.).
 is the maximum voltage
is the maximum voltage
Changing electric field causes a displacement current
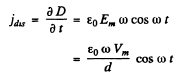
This gives rise to a magnetic field B (r) (at a radial distance r from the centre of the plate)
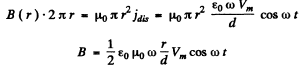
Energy associated with this field is
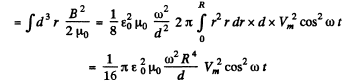
Thus the maximum magnetic energy
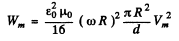
Hence
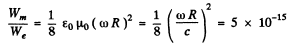
The approximation are valid only if 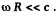
Q.202. An alternating sinusoidal current of frequency ω = = 1000 s-1 f lows in the winding of a straight solenoid whose crosssectional radius is equal to R = 6.0 cm. Find the ratio of peak values of electric and magnetic energies within the solenoid.
Ans. Here 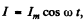 then the peak magnetic eneigy is
then the peak magnetic eneigy is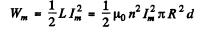
Changing magnetic field induces an electric field which by Faraday’s law is given by
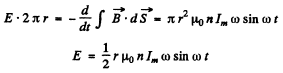
The associated peak electric eneigy is
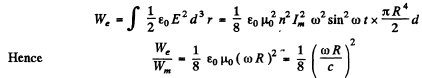
Again we expect the results to be valid if and only if
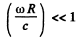
Q.203. A parallel-plate capacity whose electrodes are shaped as round discs is charged slowly. Demonstrate that the flux of the Poynting vector across the capacitor's lateral surface is equal to the increment of the capacitor's energy per unit time. The dissipation of field at the edge is to be neglected in calculations.
Ans. If the chaige on the capacitor is Q, the rate of increase of the capacitor’s energy
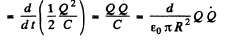
N ow electric field betw een the plates (inside it) is, 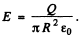
So displacement current 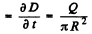
This will lead to a magnetic field, (circuital) inside the plates. At a radial distance r
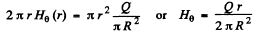
Hence 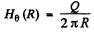 at the edge.
at the edge.
Thus inward Poynting vector 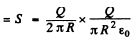
Total flow =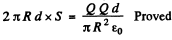
Q.204. A current I flows along a straight conductor with round cross-section. Find the flux of the Poynting vector across the lateral surface of the conductor's segment with resistance R.
Ans. Suppose the radius of the conductor is R0. Then the conduction current density is
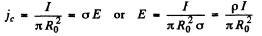
where 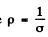 i.s the resistivity.
i.s the resistivity.
Inside the conductor there is a magnetic field given by
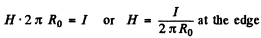
∴ Energy flowing in per second in a section of length l is
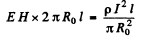
But the resistance 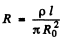
Thus the energy flowing into the conductor = I 2 R.
Q.205. Non-relativistic protons accelerated by a potential difference U form a round beam with current I. Find the magnitude and direction of the Poynting vector outside the beam at a distance r from its axis.
Ans. Here 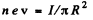 where R = radius of cross section of the conductor and n = chaige density (per unit volume)
where R = radius of cross section of the conductor and n = chaige density (per unit volume)
Also
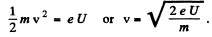
Thus, the moving protons have a charge per unit length
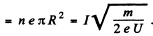
This gives rise to an electric field at a distance r given by
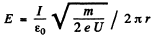
The magnetic field is 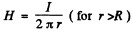
Thus
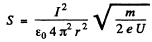 radially outward from the axis
radially outward from the axis
This is the Poynting vector.
Q.206. A current flowing in the winding of a long straight solenoid is increased at a sufficiently slow rate. Demonstrate that the rate at which the energy of the magnetic field in the solenoid increases is equal to the flux of the Poynting vector across the lateral surface of the solenoid.
Ans. Within the solenoid 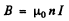 and the rate of change of magnetic energy
and the rate of change of magnetic energy
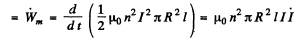
where R = radius of cross section of the solenoid l = length.
Also 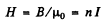 along the axis within the solenoid.
along the axis within the solenoid.
By Faraday’s law, the induced electric field is
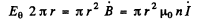
or 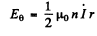
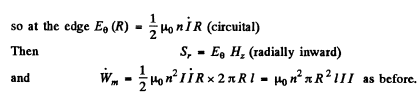
Q.207. Fig. 4.39 illustrates a segment of a double line carrying direct current whose direction is indicated by the arrows. Taking into account that the potential 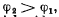 and making use of the Poynting vector, establish on which side (left or right) the source of the current is located.
and making use of the Poynting vector, establish on which side (left or right) the source of the current is located.
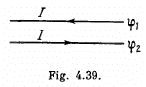
Ans. Given 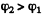
The electric field is as shown by the dashed lines (— →).
The magnetic field is as shown  emeiging out of the paper.
emeiging out of the paper.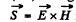 is parallel to the wires and towards right.
is parallel to the wires and towards right.
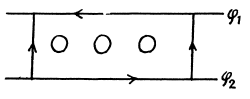
Hence source must be on the left.
Q.208. The energy is transferred from a source of constant voltage V to a consumer by means of a long straight coaxial cable with negligible active resistance. The consumed current is I. Find the energy flux across the cross-section of the cable. The conductive sheath is supposed to be thin.
Ans. The electric field (— → ) and the magnetic field (H→) are as shown. The electric field by Gauss’s theorem is like
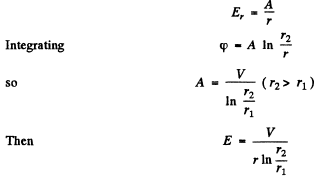

Then 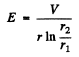
Magnetic field is 
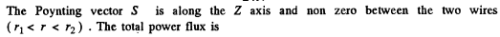

Q.209. A source of ac voltage V = Vo cos ωt delivers energy to a consumer by means of a long straight coaxial cable with negligible active resistance. The current in the circuit varies as I = = Io cos ωt — φ). Find the time-averaged energy flux through the cross-section of the cable. The sheath is thin.
Ans. As in the previous problem 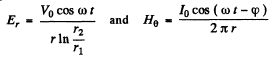
Hence time averaged power flux ( along the z axis ) = 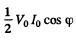
On using 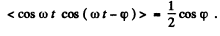
Q.210. Demonstrate that at the boundary between two media the normal components of the Poynting vector are continuous, i.e. S1n = S2n.
Ans. Let 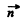 be along tbe z axis. Then
be along tbe z axis. Then
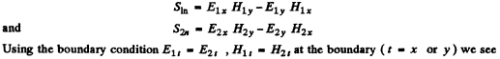
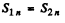
FAQs on Irodov Solutions: Electromagnetic Waves. Radiation- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are electromagnetic waves and how are they related to radiation? |  |
| 2. What are some examples of electromagnetic waves? |  |
| 3. How do electromagnetic waves propagate through space? |  |
| 4. What is the relationship between the wavelength and frequency of electromagnetic waves? |  |
| 5. How are electromagnetic waves used in everyday life? |  |





















