Irodov Solutions: Electromagnetic Waves. Radiation- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.211. Demonstrate that a closed system of charged non-relativistic particles with identical specific charges emits no dipole radiation.
Ans.
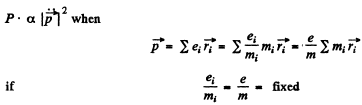
But 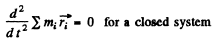
Hence P = 0
Q.212. Find the mean radiation power of an electron performing harmonic oscillations with amplitude a = 0.10 nm and frequen cy ω = 6.5.1014S-1
Ans.
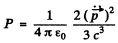
Thus 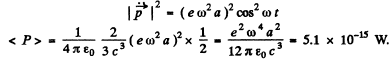
Q.213. Find the radiation power developed by a non-relativistic particle with charge e and mass m, moving along a circular orbit of radius R in the field of a stationary point charge q.
Ans. Here
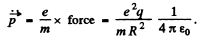
Thus 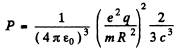
Q.214. A particle with charge e and mass m. flies with non-relativistic velocity v at a distance b past a stationary particle with charge q. Neglecting the bending of the trajectory of the moving particle, find the energy lost by this particle due to radiation during the total flight time
Ans. Most of the radiation occurs when the moving particle is closest to the stationary particle. In that region, we can write
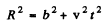
and apply the previous problem’s formula
Thus 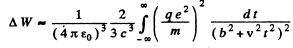
(the integral can be taken between 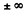 with little error.)
with little error.)
Now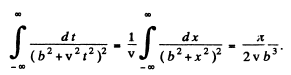
Hence,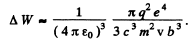
Q.215. A non-relativistic proton enters a half-space along the normal to the transverse uniform magnetic field whose induction equals B = 1.0 T. Find the ratio of the energy lost by the proton due to radiation during its motion in the field to its initial kinetic energy.
Ans. For the semicircular path on the right
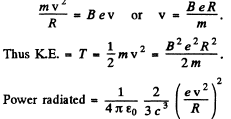
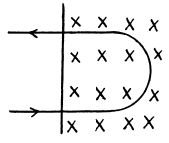
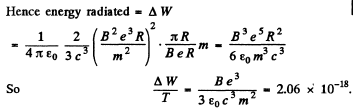
(neglecting the change in v due to radiation, correct if 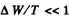 ).
).
Q.216. A non-relativistic charged particle moves in a transverse uniform magnetic field with induction B. Find the time dependence of the particle's kinetic energy diminishing due to radiation. How soon will its kinetic energy decrease e-fold? Calculate this time interval for the case
(a) of an electron,
(b) of a proton.
Ans.
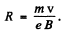
Then
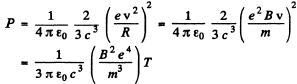
This is the radiated power so
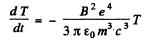
Integrating,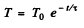
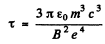
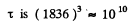 times less for an electron than for a proton so electrons radiate away their energy much faster in a magnetic field.
times less for an electron than for a proton so electrons radiate away their energy much faster in a magnetic field.
Q.217. A charged particle moves along the y axis according to the law y = a cos ωt, and the point of observation P is located on the axis at a distance 1 from the particle (l ≫ a). Find the ratio of electromagnetic radiation flow densities S1/S2 at the point P at the moments when the coordinate of the particle y1 = 0 and y2 = a. Calculate that ratio if co = 3.3.106 s--1 and l = 190 m.
Ans. P is a fixed point at a distance l from the equilibrium position of the particle. Because / > a, to first order in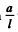 the distance between P and the instantaneous position of the particle is still l For the first case y = 0 so t = T/4
the distance between P and the instantaneous position of the particle is still l For the first case y = 0 so t = T/4
The corresponding retarded time is 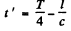
Now 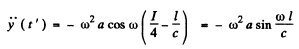
For the second case y = a at t = 0 so at the retarded time 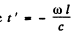
Thus 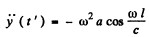
The radiation fluxes in the two cases are proportional to 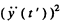
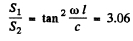 on substitution.
on substitution.
Note : The radiation received at P at time t depends on the acceleration of the charge at the retarded time.
Q.218. A charged particle moves uniformly with velocity v along a circle of radius R in the plane xy (Fig. 4.40). An observer is located
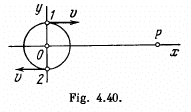
on the x axis at a point P which is removed from the centre of the circle by a distance much exceeding R. Find:
(a) the relationship between the observed values of the y projection of the particle's acceleration and the y coordinate of the particle;
(b) the ratio of electromagnetic radiation flow densities S1/S2 at the point P at the moments of time when the particle moves, from the standpoint of the observer P, toward him and away from him, as shown in the figure.
Ans. Along the circle x = sin ωt, y = cos ωt
where 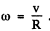 If t is the parameter in x (r), y (r) and
If t is the parameter in x (r), y (r) and
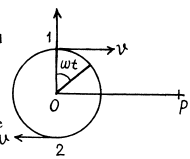
t ' is the observer time then
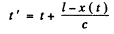
where we have neglected the effect of the y--cordinate which is of second order. The observed cordinate are
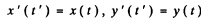
Then
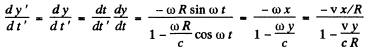
and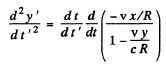
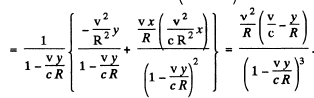
This is the observed acceleration.
(b) Energy flow density of JEM radiation S is proportional to the square of the y-projection o f the observed acceleration o f the particle 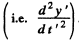
Thus 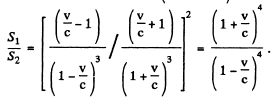
Q.219. An electromagnetic wave emitted by an elementary dipole propagates in vacuum so that in the far field zone the mean value of the energy flow density is equal to So at the point removed from the dipole by a distance r along the perpendicular drawn to the dipole's axis. Find the mean radiation power of the dipole. pole's axis. Find the mean radiation power of the dipole.
Ans. We know that
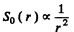
At other angles 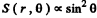
Thus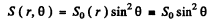
Average power radiated
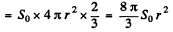
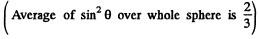
Q.220. The mean power radiated by an elementary dipole is equal to Po. Find the mean space density of energy of the electromagnetic field in vacuum in the far field zone at the point removed from the dipole by a distance r along the perpendicular drawn to the dipole's axis.
Ans.From the previous problem.
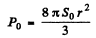
or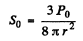
Thus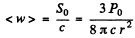
(Poynting flux vector is the energy contained is a box of unit cross section and length c).
Q.221. An electric dipole whose modulus is constant and whose moment is equal to p rotates with constant angular velocity w about the axis drawn at right angles to the axis of the dipole and passing through its midpoint. Find the power radiated by such a dipole.
Ans. The rotating dispole has moments
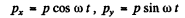
Thus
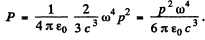
Q.222. A free electron is located in the field of a plane electromagnetic wave. Neglecting the magnetic component of the wave disturbing its motion, find the ratio of the mean energy radiated by the oscillating electron per unit time to the mean value of the energy flow density of the incident wave.
Ans. If the electric field of the wave is
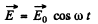
then this induces a dipole moment whose second derivative is
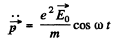
Hence radiated mean power 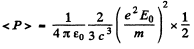
On the other hand the mean Poynting flux of the incident radiation is
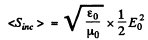
Thus
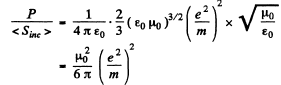
Q.223. A plane electromagnetic wave with frequency ω falls upon an elastically bonded electron whose natural frequency equals ω0. Neglecting the damping of oscillations, find the ratio of the mean energy dissipated by the electron per unit time to the mean value of the energy flow density of the incident wave.
Ans. For the elastically bound electron
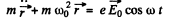
This equation has the particular integral (i.e. neglecting the part which does not have the frequency of the impressed force)
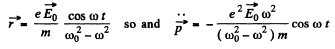
Hence P = mean radiated power
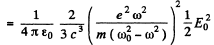
The mean incident poynting flux is
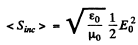
Thus
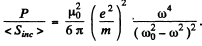
Q.224. Assuming a particle to have the form of a ball and to absorb all incident light, find the radius of a particle for which its gravitational attraction to the Sun is counterbalanced by the force that light exerts on it. The power of light radiated by the Sun equals P = 4.1026 W, and the density of the particle is p = 1.0 g/cm3
Ans. Let r = radius of the ball R = distance betw een the ball & the Sun ( r « R ) .
M = mass of the Sun
y = gravitational constant
Then
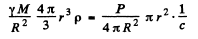
( the factor 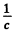 converts the energy received on the right into momentum received. Then the right hand side is the momentum received per unit time and must equal tLe negative of the impressed force for equilibrium).
converts the energy received on the right into momentum received. Then the right hand side is the momentum received per unit time and must equal tLe negative of the impressed force for equilibrium).
Thus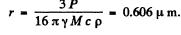

|
Explore Courses for JEE exam
|

|

















