Irodov Solutions: Elementary Particles- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.291. Calculate the kinetic energies of protons whose momenta are 0.10, 1.0, and 10 GeVic, where c is the velocity of light.
Ans. The formula is

Thus T = 5.3 MeV for 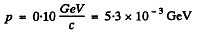
T = 0.433 GeV for
T = 9.106 GeV for 
Here we have used mo c2 = 0.938 GeV
Q.292. Find the mean path travelled by pions whose kinetic energy exceeds their rest energy η = 1.2 times. The mean lifetime of very slow pions is ζo = 25.5 ns.
Ans. Energy of pions is (1 + η) mo c2 so

Hence 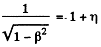 or
or 
Here 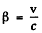 of pion. Hence time dilation factor is 1 + η and the distance traversed by the pion in its lifetime will be
of pion. Hence time dilation factor is 1 + η and the distance traversed by the pion in its lifetime will be
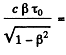
 15.0 metres
15.0 metres
on substituting the values of various quantities. (Note. The factor  can be looked at as a time dilation effect in the laboratory frame or as length contraction factor brought to the other side in the proper frame of the pion).
can be looked at as a time dilation effect in the laboratory frame or as length contraction factor brought to the other side in the proper frame of the pion).
Q.293. Negative pions with kinetic energy T = 100 MeV travel an average distance l = 11 m from their origin to decay. Find the proper lifetime of these pions.
Ans. From the previous problem
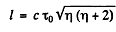
where 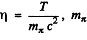 is the rest mass of pions.
is the rest mass of pions.
substitution gives 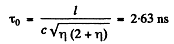

where we have used 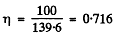
Q.294. There is a narrow beam of negative pions with kinetic energy T equal to the rest energy of these particles. Find the ratio of fluxes at the sections of the beam separated by a distance l = = 20 m. The proper mean lifetime of these pions is ζo= 25.5 ns.
Ans. here 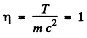 so the life time of the pion in the laboratory frame is
so the life time of the pion in the laboratory frame is

The law of radioactive decay implies that the flux decrease by the factor.
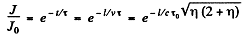

Q.295. A stationary positive pion disintegrated into a muon and a neutrino. Find the kinetic energy of the muon and the energy of the neutrino.
Ans. Energy-momentum conservation implies


But 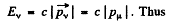

Hence 
So 


Substituting 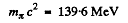
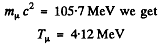
Also 
Q.296. Find the kinetic energy of a neutron emerging as a result of the decay of a stationary ∑ - hyperon (∑ - →n + π-).
Ans. We have
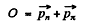 (1)
(1)
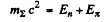
or 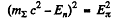
or 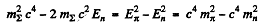
because (1) implies 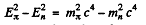
Hence 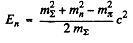
and 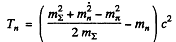

Substitution gives Tn = 19.55 MeV
Q.297. A stationary positive muon disintegrated into a positron and two neutrinos. Find the greatest possible kinetic energy of the positron.
Ans. The reaction is
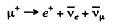
The neutrinoes are massless. The positron will carry largest momentum if both neutriones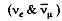 move in the same direction in the rest frame of the nuon. Then the final product is effectively a two body system and we get from problem (295)
move in the same direction in the rest frame of the nuon. Then the final product is effectively a two body system and we get from problem (295)
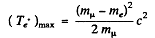
Substitution gives 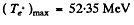
Q.298. A stationary neutral particle disintegrated into a proton with kinetic energy T = 5.3 MeV and a negative pion. Find the mass of that particle. What is its name?
Ans. By conservation of energy-momentum

Then 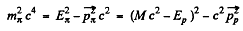
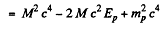
This is a quadratic equation in M 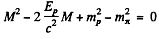
or using 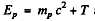 and solving
and solving

Hence, 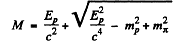
taking the positive sign. Thus

Substitution gives
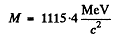
From the table of masses we identify the particle as a ∧ particle
Q.299. A negative pion with kinetic energy T = 50 MeV disintegrated during its flight into a muon and a neutrino. Find the energy of the neutrino outgoing at right angles to the pion's motion direction.
Ans. See the diagram. By conservation of eneigy
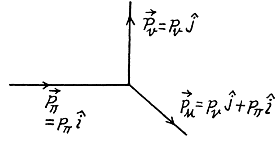
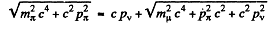
or

or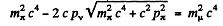
Hence the eneigy of the neutrino is
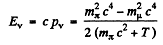
on writing 
Substitution gives Ev = 21.93 MeV
Q.300. A ∑+ hyperon with kinetic energy T∑ = 320 MeV disintegrated during its flight into a neutral particle and a positive pion outgoing with kinetic energy Tπ = 42 MeV at right angles to the hyperon's motion direction. Find the rest mass of the neutral particle (in MeV units).
Ans. By eneigy conservation
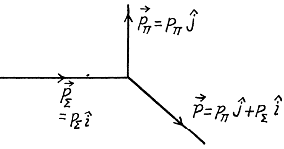

or 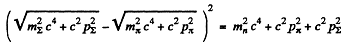
or 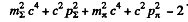
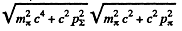

or using the K.E. of ∑ & π
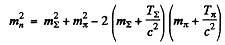
and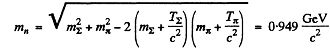
Q.301. A neutral pion disintegrated during its flight into two gamma quanta with equal energies. The angle of divergence of gamma quanta is 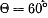 Find the kinetic energy of the pion and of each gamma quantum.
Find the kinetic energy of the pion and of each gamma quantum.
Ans. Here by conservation of momentum
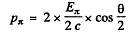
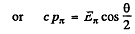
Thus 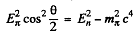
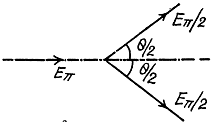
or 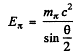
and 
substitution gives 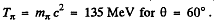
Also
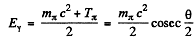
= mx c2 in this case (θ = 60°)
Q.302. A relativistic particle with rest mass m collides with a stationary particle of mass M and activates a reaction leading to formation of new particles: m + M →m1 +m2 . ..,where the rest masses of newly formed particles are written on the right-hand side. Making use of the invariance of the quantity E2 — p2c2 , demonstrate that the threshold kinetic energy of the particle m required for this reaction is defined by Eq. (6.7c).
Ans. With particle masses standing for the names of the particles, the reaction is

On R.H.S. let the energy momenta be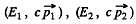 etc. On the left the energy momentum o f the particle m is
etc. On the left the energy momentum o f the particle m is 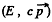 and that of the other particle is
and that of the other particle is 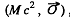 where, of course, the usual relations
where, of course, the usual relations
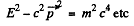
hold. From the conservation of energy momentum we see that
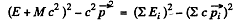
Left hand side is

We evaluate the R.H.S. in the frame where 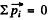 (CM frame of the decay product).
(CM frame of the decay product).
Then 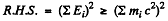
because all energies are +ve. Therefore we have the result
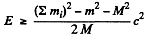
or since E = mc2 + T, we see that T ≤ Tth where
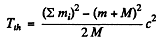
Q.303. A positron with kinetic energy T = 750 keV strikes a stationary free electron. As a result of annihilation, two gamma quanta with equal energies appear. Find the angle of divergence between them.
Ans. By momentum conservation
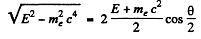
or 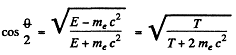
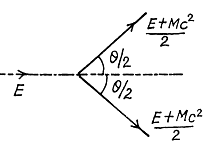
Substitution gives
θ = 98.8°
Q.304. Find the threshold energy of gamma quantum required to form (a) an electron-positron pair in the field of a stationary electron; (b) a pair of pions of opposite signs in the field of a stationary proton.
Ans. The formula of problem 3.02 gives
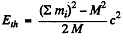
when the projectile is a photon
(a) For 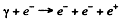
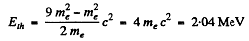
(b) For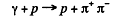


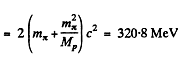
Q.305. Protons with kinetic energy T strike a stationary hydrogen target. Find the threshold values of T for the following reactions: (a)  (b)
(b) 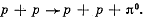
Ans. (a) For 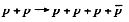
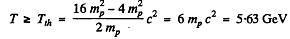
(b) For 
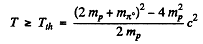

Q.306. A hydrogen target is bombarded by pions. Calculate the threshold values of kinetic energies of these pions making possible the following reactions: (a)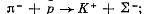 (b)
(b) 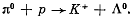
Ans. (a) Here
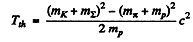
Substitution gives Tth = 0.904 GeV
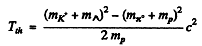
Substitution gives Tth = 0.77 GeV.
Q.307. Find the strangeness S and the hypercharge Y of a neutral elementary particle whose isotopic spin projection is Tz = +1/2 and baryon charge B = +1. What particle is this?
Ans. From the Gell-Mann Nishijima formula
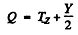
we get
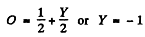
Also  . Thus the particle is =° 0.
. Thus the particle is =° 0.
Q.308. Which of the following processes are forbidden by the law of conservation of lepton charge:

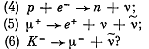
Ans. (1) The process 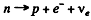 cannot occur as there are 2 more leptons
cannot occur as there are 2 more leptons 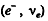 on the right comopared to zero on the left
on the right comopared to zero on the left
(2 ) The process 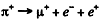 is forbidden because this corresponds to a change of lepton number by, (0 on the left - 1 on the right)
is forbidden because this corresponds to a change of lepton number by, (0 on the left - 1 on the right)
(3) The process 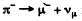 is forbidden because
is forbidden because  being both leptons ΔL = 2hre.
being both leptons ΔL = 2hre.
(4) , (5), (6) are allowed (except that one must distinguish between muon neutrinoes and electron neutrinoes). The correct names would be

Q.309. Which of the following processes are forbidden by the law of conservation of strangeness:


Ans. (1)
SO 
(2) 
SO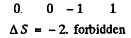
(3) 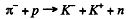
SO 
(4) 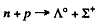
SO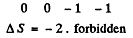
(5) 
SO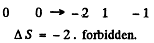
(6) 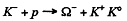
SO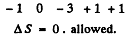
Q.310. Indicate the reasons why the following processes are forbidden:
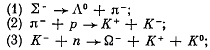

Ans. (1) 
is forbidden by energy conservation. The mass difference

(The process 1 → 2 + 3 will be allowed only if m1 > m2 + m3.)
(2) 
is disallowed by conservation of baryon number.
(3) 
is forbidden by conservation of charge
(4)
is forbidden by strangeness conservation.
(5)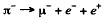
is forbidden by conservation of muon number (or lepton number).
(6)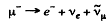
is forbidden by the separate conservation of muon number as well as lepton number.
FAQs on Irodov Solutions: Elementary Particles- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are elementary particles? |  |
| 2. How many types of elementary particles are there? |  |
| 3. What is the significance of elementary particles in physics? |  |
| 4. Can elementary particles be created or destroyed? |  |
| 5. How are elementary particles classified? |  |

|
Explore Courses for JEE exam
|

|

















