Irodov Solutions: Laws of Conservation of Energy, Momentum & Angular Momentum - 4 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 181. A spaceship of mass m0 moves in the absence of external forces with a constant velocity v0. To change the motion direction, a jet engine is switched on. It starts ejecting a gas jet with velocity u which is constant relative to the spaceship and directed at right angles to the spaceship motion. The engine is shut down when the mass of the spaceship decreases to m. Through what angle α did the motion direction of the spaceship deviate due to the jet engine operation?
Ans. 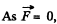 from the equation of dynamics of a body with variable mass;
from the equation of dynamics of a body with variable mass;
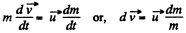 (1)
(1)
 (because v0 is constant) Where d α is the angle by which the spaceship,turns in time dt.
(because v0 is constant) Where d α is the angle by which the spaceship,turns in time dt.
So, 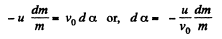
or, 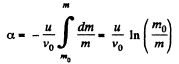
Q. 182. A cart loaded with sand moves along a horizontal plane due to a constant force F coinciding in direction with the cart's velocity vector. In the process, sand spills through a hole in the bottom with a constant velocity μ kg/s. Find the acceleration and the velocity of the cart at the moment t, if at the initial moment t = 0 the cart with loaded sand had the mass m0 and its velocity was equal to zero. The friction is to be neglected.
Ans. 
Integrating 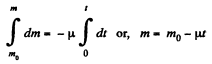
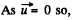 from the equation of variable mass system :
from the equation of variable mass system :

or, 
Hence 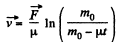
Q. 183. A flatcar of mass mo starts moving to the right due to a from a stationary hopper. The velocity of loading is constant and equal to p, kg/s. Find the time dependence of the velocity and the acceleration of the flatcar in the process of loading. The friction is negligibly small.
Ans. Let the car be moving in a reference frame to which the hopper is fixed and at any instant of time, let its mass be m and velocity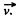
Then from the general equation, for variable mass system.
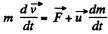
We write the equation, for our system as,
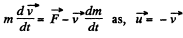 (1)
(1)
So 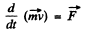
and 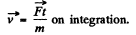
But 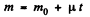
so, 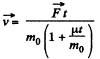
Thus the sought acceleration, 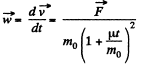
Q. 184. A chain AB of length l is located in a smooth horizontal tube so that its fraction of length h hangs freely and touches the surface of the table with its end B (Fig. 1.47). At a-certain moment the end A of the chain is set free. With what velocity will this end of the chain slip out of the tube ?

Ans. Let the length of the chain inside the smooth horizontal tube at an arbitrary instant is x. From the equation,
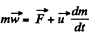
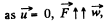 for the chain inside the tube
for the chain inside the tube
 (1)
(1)
Similarly for the overhanging,
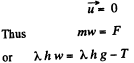 (2)
(2)
From (1) and (2
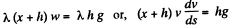
or, 

[As the length of the chain inside the tube decreases ses with time, ds = - dx.]
or, 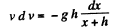
Integrating, 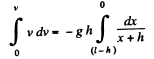
or, 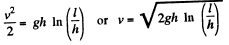
Q. 185. The angular momentum of a particle relative to a certain point 0 varies with time as M = a + bt2, where a and b are constant vectors, with a ⊥ b. Find the force moment N relative to the point O acting on the particle when the angle between the vectors N and M equals 45°.
Ans. Force moment relative to point O ;
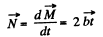
Let the angle between 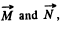
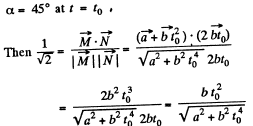

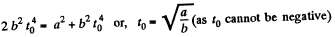
It is also obvious from the figure that the angle α is equal to 45° at the moment t0.

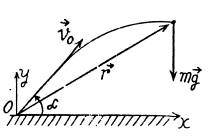
Q. 186. A ball of mass m is thrown at an angle α to the horizontal with the initial velocity v0. Find the time dependence of the magnitude of the ball's angular momentum vector relative to the point from which the ball is thrown. Find the angular momentum M at the highest point of the trajectory if m = 130 g, α = 45°, and v0 = 25 m/s. The air drag is to be neglected.
Ans. 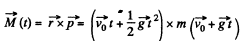
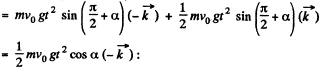
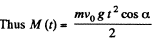
Thus angular momentum at maximum height
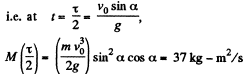
Alternate :
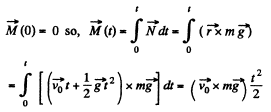
Q. 187. A disc A of mass m sliding over a smooth horizontal surface with velocity v experiences a perfectly elastic collision with a smooth stationary wall at a point O (Fig. 1.48). The angle between the motion direction of the disc and the normal of the wall is equal to α. Find:
(a) the points relative to which the angular momentum M of the disc remains constant in this process;
(b) the magnitude of the increment of the vector of the disc's angular momentum relative to the point O' which is located in the plane of the disc's motion at the distance l from the point O.
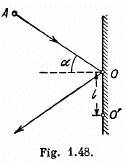
Ans. (a) The disc experiences gravity, the force of reaction of the horizontal surface, and the force  reaction of the wall at the moment of the impact against it. The first two forces counter-balance each other, leaving only the force
reaction of the wall at the moment of the impact against it. The first two forces counter-balance each other, leaving only the force  It’s moment relative to any point of the line along which the vector
It’s moment relative to any point of the line along which the vector  or along normal to the wall is equal to zero and therefore the angular momentum of the disc relative to any of these points does not change in the given process.
or along normal to the wall is equal to zero and therefore the angular momentum of the disc relative to any of these points does not change in the given process.
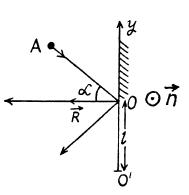
(b) During the course of collision with wall the position of disc is same and is equal to 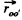 Obviously the increment in linear momentum of the ball
Obviously the increment in linear momentum of the ball 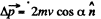
Here, 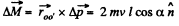 and directed normally emerging from the plane of figure
and directed normally emerging from the plane of figure
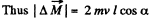
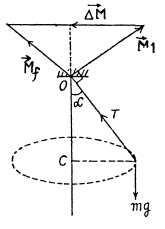
Q. 188. A small ball of mass m suspended from the ceiling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω. Relative to which points does the angular momentum M of the ball remain constant? Find the magnitude of the increment of the vector of the ball's angular momentum relative to the point O picked up during half a revolution.
Ans. (a) The ball is under the influence of forces 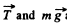 at all the moments of time, while moving along a horizontal circle. Obviously the vertical component of
at all the moments of time, while moving along a horizontal circle. Obviously the vertical component of 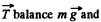 so the net moment of these two about any point becoems zero. The horizontal component of
so the net moment of these two about any point becoems zero. The horizontal component of 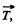 which provides the centripetal acceleration to ball is already directed toward the centre (C) of the horizontal circle , thus its moment about the point C equals zero at all the moments of time. Hence the net moment of the force acting on the ball about point C equals zero and that’s why the angular mommetum of the ball is con served about the horizontal circle.
which provides the centripetal acceleration to ball is already directed toward the centre (C) of the horizontal circle , thus its moment about the point C equals zero at all the moments of time. Hence the net moment of the force acting on the ball about point C equals zero and that’s why the angular mommetum of the ball is con served about the horizontal circle.
(b) Let a be the angle which the thread forms with the vertical.
Now from equation of particle dynamics :
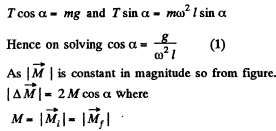
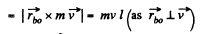
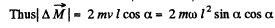
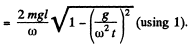
Q. 189. A ball of mass m falls down without initial velocity from a height h over the Earth's surface. Find the increment of the ball's angular momentum vector picked up during the time of falling (relative to the point O of the reference frame moving translationally in a horizontal direction with a velocity V). The ball starts falling from the point O. The air drag is to be neglected.
Ans. During the free fall time 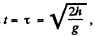 the reference point O moves in hoizontal direction (say tow ards right) b y the distance Vτ. In the translating fram e as
the reference point O moves in hoizontal direction (say tow ards right) b y the distance Vτ. In the translating fram e as 

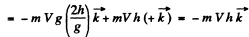

Hence 
Q. 190. A smooth horizontal disc rotates with a constant angular velocity ω about a stationary vertical axis passing through its centre, the point O. At a moment t = 0 a disc is set in motion from that point with velocity v0. Find the angular momentum M (t) of the disc relative to the point 0 in the reference frame fixed to the disc. Make sure that this angular momentum is caused by the Coriolis force.
Ans. The Coriolis force is. 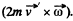
Here 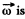 along the z-axis (vertical). The moving disc is moving with velocity v0 which is constant. The motion is along the x-axis say. Then the Coriolis force is along y-axis and has the m agnitude
along the z-axis (vertical). The moving disc is moving with velocity v0 which is constant. The motion is along the x-axis say. Then the Coriolis force is along y-axis and has the m agnitude 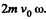 At time t, the distance of the centre of moving disc from
At time t, the distance of the centre of moving disc from 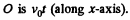 Thus the torque N due to the coriolis force is
Thus the torque N due to the coriolis force is
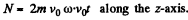
Hence equating this to 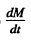
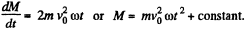
The constant is irrelevant and may be put equal to zero if the disc is originally set in motion from the point O.
This discussion is approximate. The Coriolis force will cause the disc to swerve from straight line motion and thus cause deviation from the above formula which will be substantial for large t.
Q. 191. A particle moves along a closed trajectory in a central field of force where the particle's potential energy U = kr2 (k is a positive constant, r is the distance of the particle from the centre O of the field). Find the mass of the particle if its minimum distance from the point O equals r1 and its velocity at the point farthest from 0 equals v2.
Ans. If r = radial velocity of the particle then the total .energy of the particle at any instant is
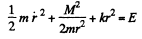 (1)
(1)
where the second term is the kinetic energy of angular motion about the centre O. Then the extreme values of r are determined by r = 0 and solving the resulting quadratic equation
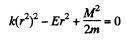
we get
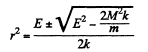
From this we see that
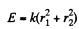 (2)
(2)
where r1 is the minimum distance from O and r2 is the maximum distance. Then
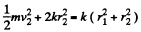
Hence, 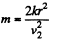
Note : Eq. (1) can be derived from the standard expression for kinetic energy and angular momentum in plane poler coordinates :
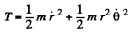
M = angular momentum = mr2θ
Q. 192. A small ball is suspended from a point O by a light thread of length l. Then the ball is drawn aside so that the thread deviates through an angle θ from the vertical and set in motion in a horizontal direction at right angles to the vertical plane in which the thread is located. What is the initial velocity that has to be imparted to the ball so that it could deviate through the maximum angle π/2 in the process of motion?
Ans. The swinging sphere experiences two forces : The gravitational force and the tension of the thread. Now, it is clear from the condition, given in the problem, that the moment of these forces about the vertical axis, passing through the point of suspension Nz = 0. Consequently, the angular momentum Mz of the sphere relative to the given axis (z) is constant.
Thus 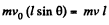 (1)
(1)
where m is the mass of the sphere and v is it s velocity in the position, when the thread 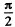 forms an angle with the vertical. Mechanical energy is also conserved, as the sphere is under the influence if only one other force, i.e. tension, which does not perform any work, as it is always perpendicular to the velocity.
forms an angle with the vertical. Mechanical energy is also conserved, as the sphere is under the influence if only one other force, i.e. tension, which does not perform any work, as it is always perpendicular to the velocity.
So,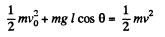 (2)
(2)
From (1) and (2), we get,
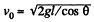
Q. 193. A small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The other end of the thread is being drawn into a hole O (Fig. 1.49) with a constant velocity. Find the thread tension as a function of the distance r between the body and the hole if at r = r0 the angular velocity of the thread is equal to ω.
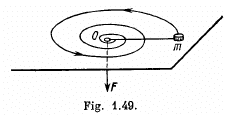
Ans. Forces, acting on the mass m are shown in the figure. As 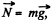 the net torque of these two forces about any tixed point must be equal to zero. Tension T, acting on the mass m is a central force, which is always directed towards the centre O. Hence the moment of force T is also zero about the point 0 and therefore the angular momentum of the particle m is conserved about O.
the net torque of these two forces about any tixed point must be equal to zero. Tension T, acting on the mass m is a central force, which is always directed towards the centre O. Hence the moment of force T is also zero about the point 0 and therefore the angular momentum of the particle m is conserved about O.
Let, the angular velocity of the particle be to, when the separation between hole and particle m is r, then from the conservation of momentum about the point O, : 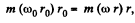
or 
Now, from the second law of motion for m,
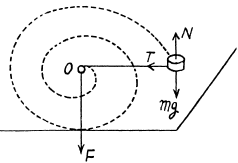
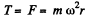
Hence the sought tension;
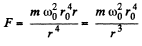
Q. 194. A light non-stretchable thread is wound on a massive fixed pulley of radius R. A small body of mass m is tied to the free end of the thread. At a moment t = 0 the system is released and starts moving. Find its angular momentum relative to the pulley axle as a function of time t.
Ans. On the given system the weight of the body m is the only force whose moment is effective about the axis of pulley. Let us take the sense of co of the pulley at an arbitrary instant  the pulley at an arbitrary instant as the positive sense of axis of rotation (z - axis)
the pulley at an arbitrary instant as the positive sense of axis of rotation (z - axis)
As 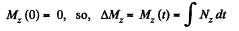
So, 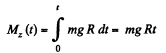
Q. 195. A uniform sphere of mass m and radius R starts rolling without slipping down an inclined plane at an angle α to the horizontal. Find the time dependence of the angular momentum of the sphere relative to the point of contact at the initial moment. How will the obtained result change in the case of a perfectly smooth inclined plane?
Ans. Let the point of contact of sphere at initial moment (t = 0) be at O. At an arbitrary moment, the forces acting on the sphere are shown in the figure. We have normal reaction Nr = mg sin a and both pass through same line and the force of static friction passes through the point O, thus the moment about point O becomes zero. Hence mg sin a is the only force which has effective torque about point 0, and is given by  mgR sin α normally emerging from the plane of figure.
mgR sin α normally emerging from the plane of figure.
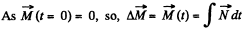
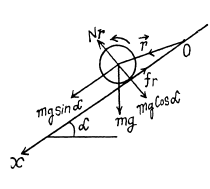
Hence , 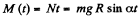
Q. 196. A certain system of particles possesses a total momentum p and an angular momentum M relative to a point O. Find its angular momentum M' relative to a point O' whose position with respect to the point O is determined by the radius vector r0. Find out when the angular momentum of the system of particles does not depend on the choice of the point O.
Ans. Let position vectors of the particles of the system be 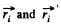 with respect to the points O and O' respectively. Then we have,
with respect to the points O and O' respectively. Then we have,
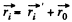 (1)
(1)
where  is the radius vector of O' with respect to O.
is the radius vector of O' with respect to O.
Now, the angular momentum of the system relative to the point O can be written as follows;
 [using (1)]
[using (1)]
or, 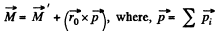 (2)
(2)
From (2), if the total linear momentum of the system, 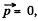 then its angular momen tum does not depend on the choice of the point O.
then its angular momen tum does not depend on the choice of the point O.
Note that in the C M . frame, the system of particles, as a whole is at rest.
Q. 197. Demonstrate that the angular momentum M of the system of particles relative to a point 0 of the reference frame K can be represented as 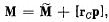
where 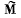 is its proper angular momentum (in the reference frame moving translationally and fixed to the centre of inertia), rc is the radius vector of the centre of inertia relative to the point O, p is the total momentum of the system of particles in the reference frame K.
is its proper angular momentum (in the reference frame moving translationally and fixed to the centre of inertia), rc is the radius vector of the centre of inertia relative to the point O, p is the total momentum of the system of particles in the reference frame K.
Ans. On the basis of solution of problem 1.196, we have concluded that; “in the C.M. frame, the angular momentum of system of particles is independent of the choice of the point, relative to which it is determined” and in accordance with the problem, this is denoted by 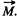
We denote the angular momentum of the system of particles, relative to the point O, by 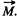 Since the internal and proper angular momentum
Since the internal and proper angular momentum 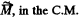 frame, does not depend on the choice of the point O', this point may be taken coincident with the point O of the A-frame, at a given moment of time. Then at that moment, the radius vectors of all the particles, in both reference frames, are equal
frame, does not depend on the choice of the point O', this point may be taken coincident with the point O of the A-frame, at a given moment of time. Then at that moment, the radius vectors of all the particles, in both reference frames, are equal  and the velocities are related by the equation,
and the velocities are related by the equation,
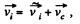 (1)
(1)
where  is the velocity of C.M. frame, relative to the A-frame. Consequently, we may write,
is the velocity of C.M. frame, relative to the A-frame. Consequently, we may write,
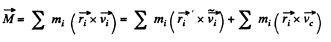
or, 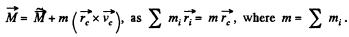
or, 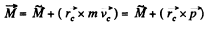
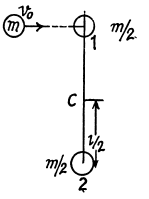
Q. 198. A ball of mass m moving with velocity v0 experiences a head-on elastic collision with one of the spheres of a stationary rigid dumbbell as whown in Fig. 1.50. The mass of each sphere equals m/2, and the distance between them is l. Disregarding the size of the spheres, find the proper angular momentum 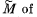 the dumbbell after the collision, i.e. the angular momentum in the reference frame moving translationally and fixed to the dumbbell's centre of inertia.
the dumbbell after the collision, i.e. the angular momentum in the reference frame moving translationally and fixed to the dumbbell's centre of inertia.
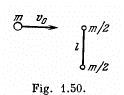
Ans. From conservation of linear momentum along the direction of incident ball for the system consists with colliding ball and phhere
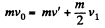
where v' and v1 are the velocities of ball and sphere 1 respectively after collision. (Remember that the collision is head on).
As the collision is perfectly elastic, from the definition of co-efficeint of restitution,
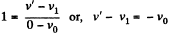 (2)
(2)
Solving (1) and (2), we get,

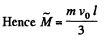
Q. 199. Two small identical discs, each of mass m, lie on a smooth horizontal plane. The discs are interconnected by a light non-deformed spring of length l0 and stiffness x. At a certain moment one of the discs is set in motion in a horizontal direction perpendicular to the spring with velocity v0. Find the maximum elongation of the spring in the process of motion, if it is known to be considerably less than unity.
Ans. In the C.M. frame of the system (both the discs + spring), the linear momentum of the discs are related by the relation,  at all the moments of time.
at all the moments of time.
where, 
And the total kinetic energy of the system,
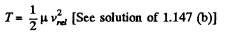
Bearing in mind that at the moment of maximum deformation of the spring, the projection of  along the length of the spring becomes zero, i.e.
along the length of the spring becomes zero, i.e. 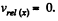
The conservation of mechanical energy of the considered system in the C.M. frame gives.
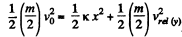 (1)
(1)
Now from the conservation of angular momentum of the system about the C.M.,

or, 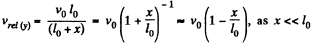 (2)
(2)
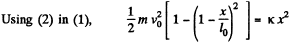
or, 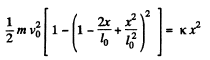
or, 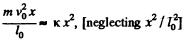
As 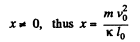
FAQs on Irodov Solutions: Laws of Conservation of Energy, Momentum & Angular Momentum - 4 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the law of conservation of energy? |  |
| 2. What is the law of conservation of momentum? |  |
| 3. What is the law of conservation of angular momentum? |  |
| 4. How are the laws of conservation of energy, momentum, and angular momentum related? |  |
| 5. Can the laws of conservation of energy, momentum, and angular momentum be violated? |  |

|
Explore Courses for JEE exam
|

|

















