Irodov Solutions: Mechanical Oscillations- 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.21. A pendulum clock is mounted in an elevator car which starts going up with a constant acceleration w, with w < g. At a height h the acceleration of the car reverses, its magnitude remaining constant. How soon after the start of the motion will the clock show the right time again?
Ans. Let the downward acceleration of the elevator car has continued for time t then the sought time
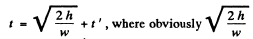 is the time of upward acceleration of the elevator.
is the time of upward acceleration of the elevator.
One should i/ote that if the point of suspension of a mathematical pendulum moves with an acceleration 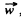 then the time period of the pendulum becomes
then the time period of the pendulum becomes
 ( see 4.30)
( see 4.30)
In this problem the time period of the pendulum while it is moving upward with acceleration w becomes
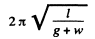 and its time period while the elevator moves downward with the same magnitude of acceleration becomes
and its time period while the elevator moves downward with the same magnitude of acceleration becomes
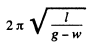
As the time of upward acceleration equals 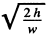 , the total number of oscillations during this time equals
, the total number of oscillations during this time equals
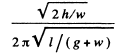
Thus the indicated time 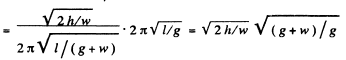
Similarly the indicated time for the time interval t '
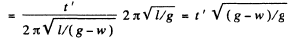
we demand that
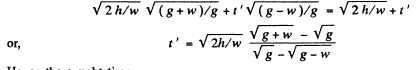
Hence the sought time
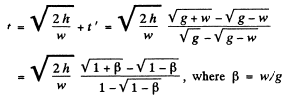
Q.22. Calculate the period of small oscillations of a hydrometer (Fig. 4.2) which was slightly pushed down in the vertical direction. The mass of the hydrometer is m = 50 g, the radius of its tube is r = 3.2 mm, the density of the liquid is ρ = 1.00 g/cm3. The resistance of the liquid is assumed to be negligible.
Ans. If the hydromoter were in equlibrium or floating, its weight will be balanced by the buoyancy force acting on it by the fluid. During its small oscillation, let us locate the hydrometer when it is at a vertically downward distance x from its equilibrium position. Obviously the net unbalanced force on the hydrometer is the excess buoyancy force directed upward and equals π r2 x ρ g. Hence for the hydrometer.
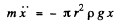
or 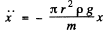
Hence the sought time period
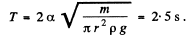
Q.23. A non-deformed spring whose ends are fixed has a stiffness x = 13 N/m. A small body of mass m = 25 g is attached at the point removed from one of the ends by η = 1/3 of the spring's length. Neglecting the mass of the spring, find the period of small longitudinal oscillations of the body. The force of gravity is assumed to be absent.
Ans. At first let us calculate the stiffness k1 and k2 of both the parts of the spring. If we subject the original spring of stiffness k having the natural length l0 (say), under the deforming forces F - F (say) to elongate the spring by the amount x y then
F = k x (1)
Therefore the elongation per unit length of the spring is x / l0 . Now let us subject one o f the parts of the spring of natural length η\ l0 under the same deforming forces F - F. Then the elongation of the spring will be
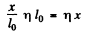
Thus 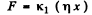 (2)
(2)
Hence from Eqns (1) and (2)
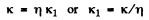
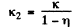
Hence the sought time period
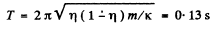
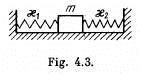
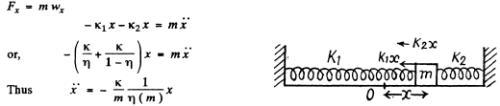
Q.24. Determine the period of small longitudinal oscillations of a body with mass m in the system shown in Fig. 4.3. The stiffness values of the springs are x1 and x2. The friction and the masses of the springs are negligible.
Ans. Similar to the Soln of 4.23, the net unbalanced force on the block m when it is at a small horizontal distance x from the equilibrium position becomes (k1 + k2)x.

Alternate : Let us set the block m in motion to perform small oscillation. Let us locate the block when it is at a distance x from its equilibrium position.
As the spring force is restoring conservative force and deformation of both the springs are same, so from the conservation of mechanical energy of oscillation of the spring-block system :
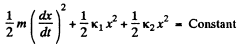
Differentiating with respect to time
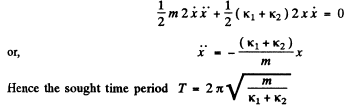
Q.25. Find the period of small vertical oscillations of a body with mass m in the system illustrated in Fig. 4.4. The stiffness values of the springs are x1 and x2, their masses are negligible.
Ans. During the vertical oscillation let us locate the block at a vertical down distance x from its equilibrium position. A t this m om ent if x1 and x2 are the additional or further elongation of the upper & lower springs relative to the equilibrium position, then the net unbalanced force on the block will be k2 x2 directed in upward direction. Hence
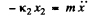 (1)
(1)
We also have x = x1 + x2 (2)
As the springs are massless and initially the net force on the spring is also zero so for the spring
k1x1 = k2x2 (3)
Solving the Eqns (1), (2) and (3) simultaneously, we get
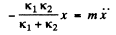
Thus 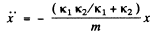
Hence the sought time period 
Q.26. A small body of mass in is fixed to the middle of a stretched string of length 2/. In the equilibrium position the string tension is equal to To. Find the angular frequency of small oscillations of the body in the transverse direction. The mass of the string is negligible, the gravitational field is absent.
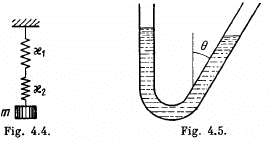
Ans.The force F, acting on the weight deflected from the position of equilibrium is 2 T0 sin θ.
Since the angle θ is small, the net restoring force, 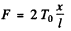

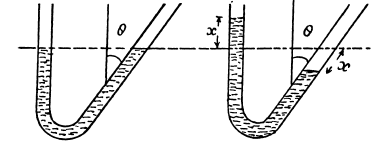
4.27. Determine the period of oscillations of mercury of mass m = 200 g poured into a bent tube (Fig. 4.5) whose right arm forms an angle θ = 30° with the vertical. The cross-sectional area of the tube is S = 0.50 cm2. The viscosity of mercury is to be neglected.
Ans. If the mercury rises m the left arm by x it m ust fall by a slanting length equal to x in the other arm.
Total pressure difference in the two arms will then be ρg x + pgx cosθ = ρgx (1 + cosθ)
This will give rise to a restoring force - ρgSx (1+ cosθ)
This must equal mass times acceleration which can be obtained from work energy principle.
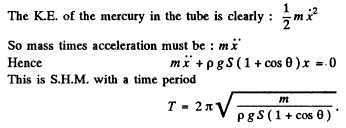
Q. 28. A uniform rod is placed on two spinning wheels as shown in Fig. 4.6. The axes of the wheels are separated by a distance l = 20 cm, the coefficient of friction between the rod and the wheels is k = 0.18. Demonstrate that in this case the rod performs harmonic oscillations. Find the period of these oscillations.
Ans. In the equilibrium position the C.M. of the rod lies nid way between the two rotating wheels. Let us displace the rod horizontally by some small distance and then release it Let us depict the forces acting on the rod when its C.M. is at distance x from its equilibrium position (Fig.). Since there is no net vertical force acting on the rod, Newton’s second law gives :
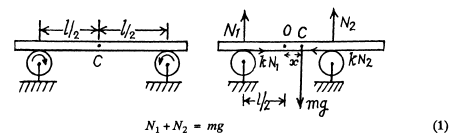
For the translational motion of the rod from the Eqn. : Fx = m wcx
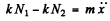 (2)
(2)
As the rod experiences no net torque about an axis perpendicular to the plane of the Fig. through the C.M. of the rod.
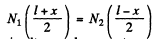 (3)
(3)
Solving Eqns. (1), (2) and (3) simultaneously we get

Hence the sought time period
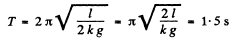
Q.29. Imagine a shaft going all the way through the Earth from pole to pole along its rotation axis. Assuming the Earth to be a homogeneous ball and neglecting the air drag, find:
(a) the equation of motion of a body falling down into the shaft;
(b) how long does it take the body to reach the other end of the shaft;
(c) the velocity of the body at the Earth's centre.
Ans. (a) The only force acting on the ball is the gravitational force 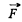 of magnitude
of magnitude 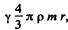 where y is the gravitational constant ρ, the density of the Earth and r is the distance of the body from the centre of the Earth.
where y is the gravitational constant ρ, the density of the Earth and r is the distance of the body from the centre of the Earth.
But, 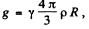 so the expression for
so the expression for 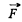 can be written as,
can be written as,
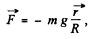 here R is the radius of the Earth and the equation of motion in projection
here R is the radius of the Earth and the equation of motion in projection
form has the form, or, 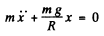
(b) The equation, obtained above has the form of an equation of S.H.M. hawing the time period,
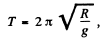
Hence the body will reach the other end of the shaft in the time,
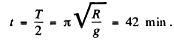
(c) From the conditions of the speed of the body at the centre of the Earth will be maximum, having the magnitude,
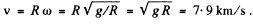
Q.30. Find the period of small oscillations of a mathematical pendulum of length 1 if its point of suspension 0 moves relative to the Earth's surface in an arbitrary direction with a constant acceleration w (Fig. 4.7). Calculate that period if l = 21 cm, ω = g/2, and the angle between the vectors w and g equals β = 120°.
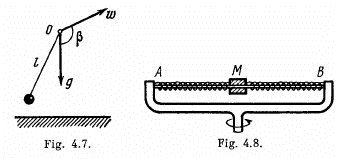
Ans. In the frame of point of suspension the mathematical pendulum of mass m (say) will oscillate. In this frame, the body m will experience the inertial force 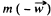 in addition to the real forces during its oscillations. Therefore in equilibrium position m is deviated by some angle say a. In equilibrium position
in addition to the real forces during its oscillations. Therefore in equilibrium position m is deviated by some angle say a. In equilibrium position
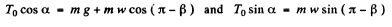
So, from these two Eqns
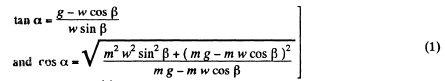
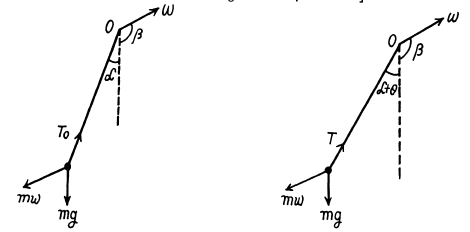
Let us displace the bob m from its equilibrium position by some small angle and then release it Now locate die ball at an angular position (α + θ) from vertical as shown in the figure.
From the Eqn. :
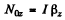
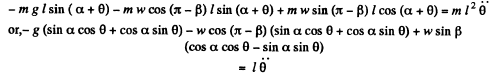
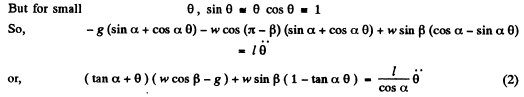
Solving Eqns (1) and (2) simultaneously we get
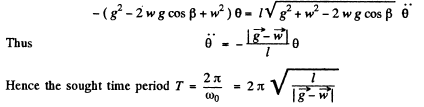
4.31. In the arrangement shown in Fig. 4.8 the sleeve M of mass m = 0.20 kg is fixed between two identical springs whose combined stiffness is equal to x = 20 N/m. The sleeve can slide without friction over a horizontal bar AB. The arrangement rotates with a constant angular velocity ω = 4.4 rad/s about a vertical axis passing through the middle of the bar. Find the period of small oscillations of the sleeve. At what values of ω will there be no oscillations of the sleeve?
Ans. Obviously the sle e v e performs small oscillations in the frame of rotating rod. In the rod’s frame let us depict the forces acting on the sleeve along the length of the rod while the sleeve is at a small distance x towards right from its equilibrium position. The free body diagram of block does not contain Coriolis force, because it is perpendicualr to the length of the rod.
From Fx - mwx for the sleeve in the frame of rod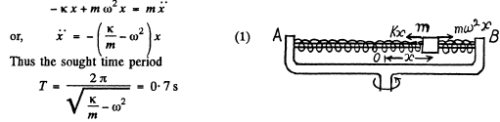
It is obvious from Eqn (1) that the sleeve will not perform small oscillations if
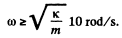
Q.32. A plank with a bar placed on it performs horizontal harmonic oscillations with amplitude a = 10 cm. Find the coefficient of friction between the bar and the plank if the former starts sliding along the plank when the amplitude of oscillation of the plank becomes less than T = 1.0 s.
Ans. When the bar is about to start sliding along the plank, it experiences the maximum restoring force which is being provided by the limiting friction, Thus
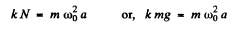
or, 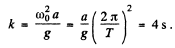
Q.33. Find the time dependence of the angle of deviation of a mathematical pendulum 80 cm in length if at the initial moment the pendulum
(a) was deviated through the angle 3.0° and then set free without push;
(b) was in the equilibrium position and its lower end was imparted the horizontal velocity 0.22 m/s;
(c) was deviated through the angle 3.0° and its lower end was imparted the velocity 0.22 m/s directed toward the equilibrium position.
Ans. The natural angular frequency of a mathematical pendulum equals

(a) We have the solution of S.H.M. equation in angular form :
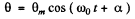
If at the initial moment i.e. at t = 0 , θ = θm than α = 0.
Thus the above equation takes the form
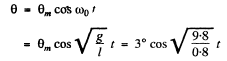
Thus 0 = 3° cos 3.5 t
(b) The S.H.M. equation in angular form :
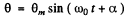
If at the initial moment t = 0 , θ = 0 , then α = 0 .Then the above equation takes the form
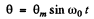
Let v0 be the velocity of the lower end of pendulam at θ = 0, then from conserved of mechanical energy of oscillaton
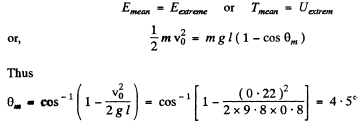
Thus the sought equation becomes
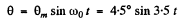
(c) Let θO and v0 be the angular deviation and linear velocity at t = 0.
As the mechanical energy of oscillation of the mathematical pendulum is conservation
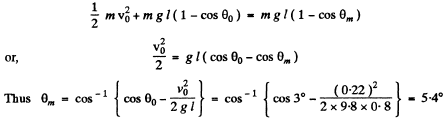
Then from θ = 5.4° sin (3.5 t + α), we see that  because the velovity is directed towards the centre. Thus
because the velovity is directed towards the centre. Thus
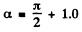 radians and we get the answer.
radians and we get the answer.
Q.34. A body A of mass m1 = 1.00 kg and a body B of mass m2 = 4.10 kg are interconnected by a spring as shown in Fig. 4.9. The body A performs free vertical harmonic oscillations with amplitude a = 1.6 cm and frequency = 25 s-1. Neglecting the mass of the spring, find the maximum and minimum values of force that this system exerts on the bearing surface.
Ans. While the body A is at its upper extreme position, the spring is obviously elongated by the amount
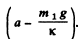
If we indicate y-axis in vertically downward direction, Newton’s second law of motion in projection form i.e. Fy = mwy for body A gives :
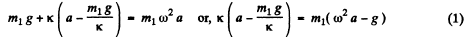
(Because at any extreme position the magnitude of acceleration of an oscillating body equals ω2a and is restoring in nature.)
If N be the normal force exerted by the floor on the body B, while the body A is at its upper extreme position, from Newton’s second law for body B
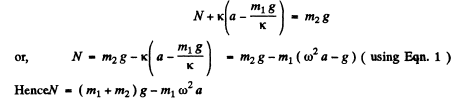
When the body A is at its lower extreme position, the spring is compresed by the distance
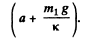
From Newton’s second law in projeciton fonn i.e. Fy = mwy for body A at this state:
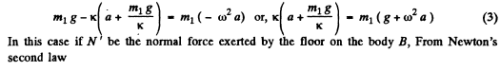
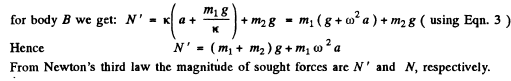
Q.35. A plank with a body of mass m placed on it starts moving straight up according to the law y = a (1 — cos ωt), where y is the displacement from the initial position, ω = 11 s -1 .

Find: (a) the time dependence of the force that the body exerts on the plank if a = 4.0 cm; plot this dependence;
(b) the minimum amplitude of oscillation of the plank at which the body starts falling behind the plank;
(c) the amplitude of oscillation of the plank at which the body springs up to a height h = 50 cm relative to the initial position (at the moment t = 0).
Ans. (a) For the block from Newton’s second law in projection form Fy = mwy
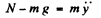 (1)
(1)
But from y = a (1 - cos ωt)
We get  (2)
(2)
From Eqns (1) and (2)
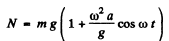 (3)
(3)
From Newtons’s third law the force by which the body m exerts on the block is directed vertically downward and equls
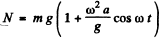
(b) When the body m starts, falling behind the plank or looking contact, N = 0, (because the normal reaction is the contact force). Thus from Eqn. (3)
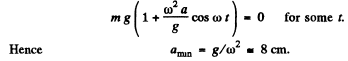
(c) We observe that the motion takes place about the mean position y = a. A t the initial instant y = 0. As shown in (b) the normal reaction vanishes at a height (g/ω2) above the position of equilibrium and the body flies off as a free body. The speed of the body at a distance (g/ω2) from the equilibrium position is  so that the condition of the problem gives
so that the condition of the problem gives
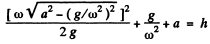
Hence solving the resulting quadratic equation and taking the positive roof,
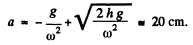
FAQs on Irodov Solutions: Mechanical Oscillations- 3 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are mechanical oscillations? |  |
| 2. How do you calculate the period of a mechanical oscillation? |  |
| 3. What is the relationship between frequency and period in mechanical oscillations? |  |
| 4. How does damping affect mechanical oscillations? |  |
| 5. What are some real-life applications of mechanical oscillations? |  |

|
Explore Courses for JEE exam
|

|

















