Irodov Solutions: Mechanical Oscillations- 4 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.36. A body of mass in was suspended by a non-stretched spring, and then set free without push. The stiffness of the spring is x. Neglecting the mass of the spring, find:
(a) the law of motion y (t) , where y is the displacement of the body from the equilibrium position;
(b) the maximum and minimum tensions of the spring in the process of motion.
Ans. (a) Let y (t) = displacement o f the body from the end of the unstreched position of the spring (not the equilibrium position). Then
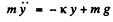
This equation has the solution of the form
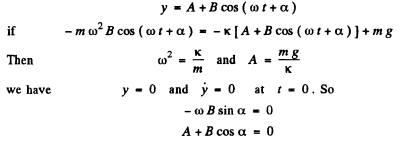
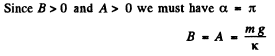
and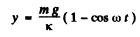
(b) Tension in the spring is
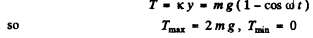
Q.37. A particle of mass in moves due to the force F = — αmr, where α is a positive constant, r is the radius vector of the particle relative to the origin of coordinates. Find the trajectory of its motion if at the initial moment r = roi and the velocity v = voj, where i and j are the unit vectors of the x and y axes.
Ans. In accordance with the problem
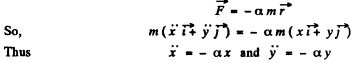
Hence the solution of the differential equation
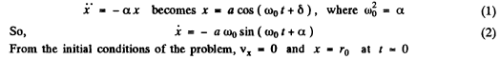
So from Eqn. (2) a - 0, and Eqn takes the form
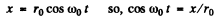 (3)
(3)
One o f the solution of the other differential Eqn 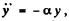 becomes
becomes
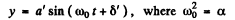 (4)
(4)
From the initial condition, y = 0 at t = 0, so δ' = 0 and Eqn (4) becomes
y = a' sin ω0t(S)
Differentiating w.r.t time we get
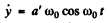 (6)
(6)
But from the initial condition of the problem, 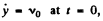

Using it in Eqn (5), we get
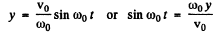 (7)
(7)
Squaring and adding Eqns (3) and (7) we get :
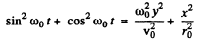
or, 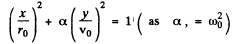
Q.38. A body of mass m is suspended from a spring fixed to the ceiling of an elevator car. The stiffness of the spring is x. At the moment t = 0 the car starts going up with an acceleration ω. Neglecting the mass of the spring, find the law of motion y (t) of the body rela- tive to the elevator car if y (0) = 0 and 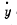 (0) = 0. Consider the following two cases:
(0) = 0. Consider the following two cases:
(a) ω = const;
(b) ω = αt, where α is a constant.
Ans. (a) As the elevator car is a translating non-inertial frame, therefore the body m will experience an inertial force m w directed downward in addition to the real forces in the elevator’s frame. From the Newton’s second law in projection form Fy = mwy for the body in the frame of elevator car:
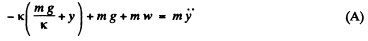
(Because the initial elongation in the spring is m g/K)
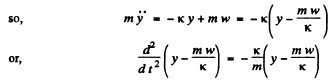 (1)
(1)
Eqn. (1) shows that the motion of the body m is S.H.M. and its solution becomes
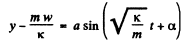 (2)
(2)
Differentiating Eqn (2) w.r.t time
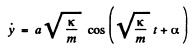 (3)
(3)
Using the initial condition y (0) = 0 in Eqn (2), we get :
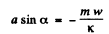
and using the other initial condition 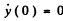 in Eqn (3)
in Eqn (3)
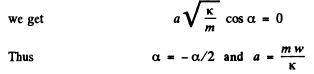
Hence using these values in Eqn (2), we get
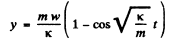
(b) Proceed up to Eqn.(l). The solution of this differential Eqn be of the form
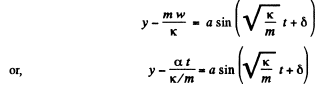
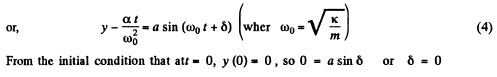
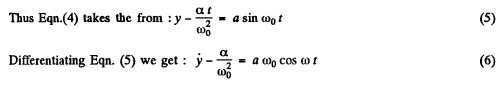
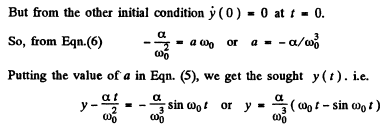
Q.39. A body of mass m = 0.50 kg is suspended from a rubber cord with elasticity coefficient k = 50 Is17m. Find the maximum distance over which the body can be pulled down for the body's oscillations to remain harmonic. What is the energy of oscillation in this case?
Ans. There is an important difference between a rubber cord or steel coire and a spring. A spring can be pulled or compressed and in both cases, obey’s Hooke’s law. But a rubber cord becomes loose when one tries to compress it and does not then obey Hooke’s law. Thus if we suspend a 'body by a rubber cord it stretches by a distance m g/k in reaching the equilibrium configuration. If we further strech it by a distance A hit will execute harmonic oscillations when released if A h ≤ m g / k because only in this case will the cord remain taut and obey Hooke’s law.
Thus A hmax ≤ m g / k
The energy of oscillation in this case is
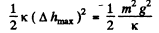
Q.40. A body of mass m fell from a height h onto the pan of a spring balance (Fig. 4.10). The masses of the pan and the spring are negligible, the stiffness of the latter is x. Having stuck to the pan, the body starts performing harmonic oscillations in the vertical direction. Find the amplitude and the energy of these oscillations.
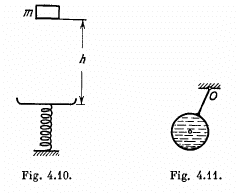
Ans. As the pan is of negligible mass, there is no loss of kinetic energy even though the collision is inelastic. The mechanical energy of the body m in the field generated by the joint action of both the gravity force and the elastic force is conserved i.e. ΔE = 0. During the motion of the body m from the initial to the final (position of maximum compression of the spring) position ΔT = 0, and therefore

or 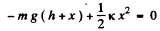
On solving the quadratic equation :
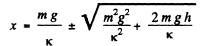
As minus sign is not acceptable
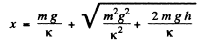
If the body m were at rest on the spring, the corresponding position of m will be its equilibrium position and at this position the resultant force on the body m will be zero. Therefore the equilibrium compression Δx (say) due to the body m will be given by
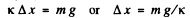
Therefore seperation between the equilibrium position and one of the extreme position i.e. the sought amplitude
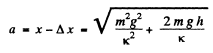
The mechanical eneigy of oscillation which is con served equals E = Uextreme, because at the extreme position kinetic eneigy becomes zero.
Although the weight of body mis aconservative force , it is not restoring in this problem , hence Uextreme is only concerned w jth the spring force . Therefore
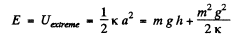
Q.41. Solve the foregoing problem for the case of the pan having a mass M. Find the oscillation amplitude in this case.
Ans. Unlike the previous (4.40) problem thekinetic energy of body m decreases due to the perfectly inelastic collision with the pan.Obviously the body m comes to strike the pan with velocity 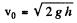 . If v be the common velocity of the " body m + pan " system due to the collision then from the conservation of linear momentum
. If v be the common velocity of the " body m + pan " system due to the collision then from the conservation of linear momentum
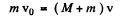
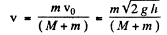
At the moment the body m strikes the pan, the spring is com pressed due to the weight of "he pan by the amount M g/ k . If l be the further com pression o f the spring due to the velocity acquired by the "pan - body m " system , then from the conservation of m echanical energy of the said system in the Geld generatad by the joint action of both the gravity and spring forces
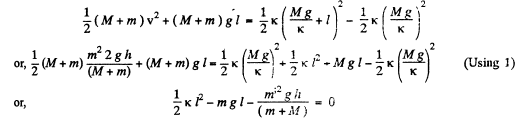
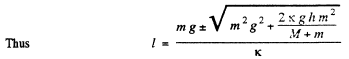
As minus sign is not acceptable
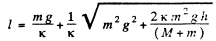
If the oscillating " pan + body m" system were at rest it correspond to their equilbijium position i.e. the spring were com pressed by 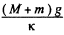 therefore the am plitude of oscillation
therefore the am plitude of oscillation

The mechanical energy of oscillation which is only conserved with the restoring forces becomes 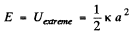 (Because spring force is the only restoring force not the weight of the body)
(Because spring force is the only restoring force not the weight of the body)
Alternately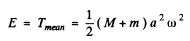
thus 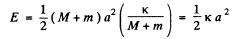
Q.42. A particle of mass m moves in the plane xy due to the force varying with velocity as 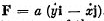 , where a is a positive constant, i and j are the unit vectors of the x and y axes. At the initial moment t = 0 the particle was located at the point x = y = 0 and possessed a velocity v0 directed along the unit vector j. Find the law of motion x (t) , y (t) of the particle, and also the equation of its trajectory.
, where a is a positive constant, i and j are the unit vectors of the x and y axes. At the initial moment t = 0 the particle was located at the point x = y = 0 and possessed a velocity v0 directed along the unit vector j. Find the law of motion x (t) , y (t) of the particle, and also the equation of its trajectory.
Ans.
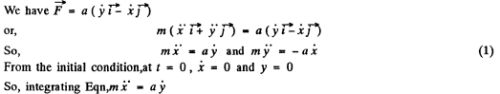
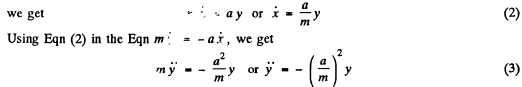
one of the solution of differential Eqn (3) is y = A sin ( ω0t + α ) , where ω0 = a/ m .
As at r = 0 ,y » 0 , s o the solution takes the form y = A sin ω0t
On differentiating w.r.t time 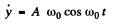
From the initial condition of the problem, at 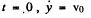
So 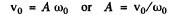
Thus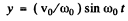 (4)
(4)
Thus from (2) 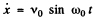 so integrating
so integrating
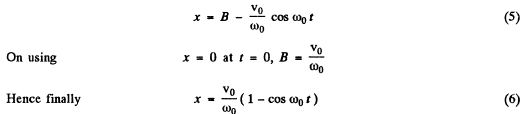
Hence from Eqns (4) and (6) we get
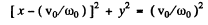
which is the equation of a circle of radius (Vo/ω0) with the centre at the point
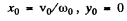
Q.43. A pendulum is constructed as a light thin-walled sphere of radius R filled up with water and suspended at the point 0 from a light rigid rod (Fig. 4.1.1). The distance between the point 0 and the centre of the sphere is equal to l. How many times will the small oscillations of such a pendulum change after the water freezes? The viscosity of water and the change of its volume on freezing are to be neglected.
Ans. If water has frozen, the system consisting of the light rod and the frozen water in the hollow sphere constitute a compound (physical) pendulum to a very good approximation because we can take the whole system to be rigid. For such systems the time period is given by
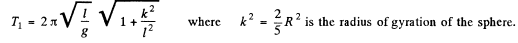
The situation is different when water is unfrozen. When dissipative forces (viscosity) are neglected, we are dealing with ideal fluids. Such fluids instantaneously respond to (unbalanced) internal stresses. Suppose the sphere with liquid water actually executes small rigid oscillations. Then the portion of the fluid above the centre of the sphere will have a greater acceleration than the portion below the centre because the linear acceleration of any element is in this case, equal to angular acceleration of the element multiplied by the distance of the element from the centre of suspension (Recall that we are considering small oscillations).
Then, as is obvious in a frame moving with the centre of mass, there will appear an unbalanced couple (not negated by any pseudoforces) which will cause the fluid to move rotationally so as to destroy differences in acceleration. Thus for this case of ideal fluids the pendulum must move in. such a way that the elements of the fluid all undergo the same acceleration. This implies that we have a simple (mathematical) pendulum with the time period :
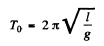
Thus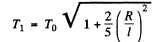
(One expects that a liquid with very small viscosity will have a time period close T0 while one with high viscosity will have a time period closer to 7l.)
Q.44. Find the frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point 0 (Fig. 4.12). The combined stiffness of the springs is equal to x. The mass of the springs is negligible.
Ans. Let us locate the rod at the position when it makes an angle 0 from the vertical. In this problem both, the gravity and spring forces are restoring conservative forces, thus from the conservation of mechanical energy of oscillation of the oscillating system :
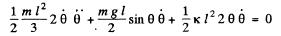 = constant
= constant
Differentiating w.r.t. time, we get :
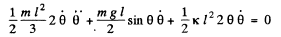
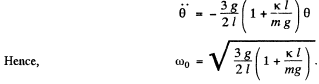
Q.45. A uniform rod of mass m = 1.5 kg suspended by two identical threads l = 90 cm in length (Fig. 4.13) was turned through a small angle about the vertical axis passing through its middle point C. The threads deviated in the process through an angle α = 5.0°. Then the rod was released to start performing small oscillations. Find:
(a) the oscillation period;
(b) the rod's oscillation energy.
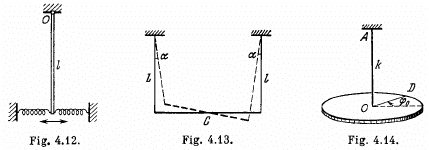
Ans. (a) Let us locate the system when the threads are deviated through an angle α' < α , during the oscillations of the system (Fig.). From the conservation of mechanical energy of the system :

Where L is the length of the rod, 0 is the angular deviation of the rod from its equilibrium position i.e. θ = 0.
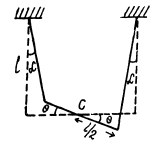
Differentiating Eqn. (1) w.r.t. time
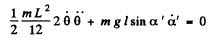
So, 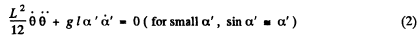
But from the Fig.
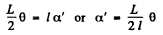
so, 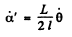
Putting these values of  in Eqn. (2) we get
in Eqn. (2) we get
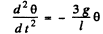
Thus the sought time period
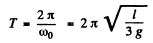
(b) The sought oscillation energy
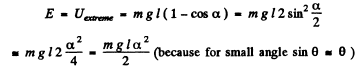
Q.46. An arrangement illustrated in Fig. 4.14 consists of a horizontal uniform disc D of mass m and radius R and a thin rod AO whose torsional coefficient is equal to k. Find the amplitude and the energy of small torsional oscillations if at the initial moment the disc was deviated through an angle φ0 from the equilibrium position and then imparted an angular velocity 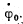
Ans.
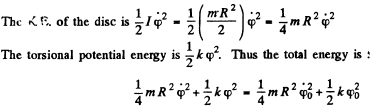
By definition of the amplitude 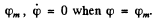 Thus total energy is
Thus total energy is
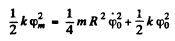
or, 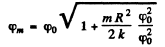
Q.47. A uniform rod of mass m and length l performs , small oscillations about the horizontal axis passing through its upper end. Find the mean kinetic energy of the rod averaged over one oscillation period if at the initial moment it was deflected from the vertical by an angle θ0 and then imparted an angular velocity 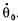 .
.
Ans. Moment of inertia of the rod equals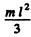 about its one end and perpendicular to its length
about its one end and perpendicular to its length
Thus rotational k inetic energy o f the rod =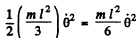
when the rod is displaced by an angle 6 its C.G. goes up by a distance
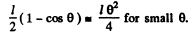
Thus the P.E. becomes : 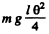
As the mechanical energy of oscillation of the rod is conserved.
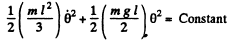
on differentiating w x t time and for the simplifies we get: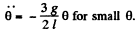
we see that the angular frequency ω is
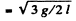
we write the general solution of the angular oscillation as:
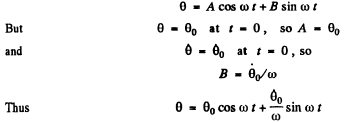
Thus the ICE. of the rod
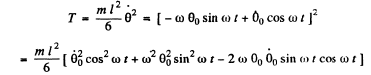
On averaging over one time period the last term vanishes and
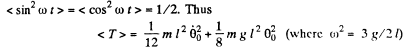
Q.48. A physical pendulum is positioned so that its centre of gravity is above the suspension point. From that position the pendulum started moving toward the stable equilibrium and passed it with an angular velocity ω. Neglecting the friction find the period of small oscillations of the pendulum.
Ans. Let l = distance between the C.G. (C) of the pendulum and, its point of suspension 0 Originally the pendulum is in inverted position and its C.G. is above O. When it falls to the normal (stable) position of equilibrium its C.G. has fallen by a distance 2l. In the equilibriun
position the total energy is equal to K.E. =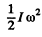 and we have from energy conservation :
and we have from energy conservation :
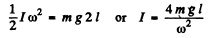
Angular frequency o f oscillation for a physical pendulum is given by 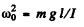
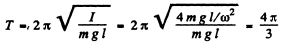
Q.49. A physical pendulum performs small oscillations about the horizontal axis with frequency ω1 = 15.0 s- 1 . When a small body of mass m = 50 g is fixed to the pendulum at a distance l = 20 cm below the axis, the oscillation frequency becomes equal to ω2 = 10.0 s-1. Find the moment• of inertia of the pendulum relative to the oscillation axis.
Ans. Let, moment of inertia of the pendulum, about the axis, concerned is 7, then writing Nz - IβD for the pendulum,
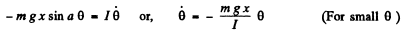
which is the required equation for S.H.M. So, the frequency of oscillation,
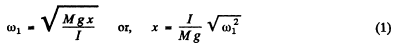
Now, when the mass m is attached to the pendulum, at a distance / below the oscillating axis,
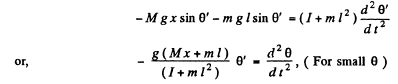
which is again the equation of S.H.M., So, the new frequency,
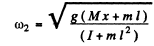 ( 2)
( 2)
Solving Eqns. (1) and (2),
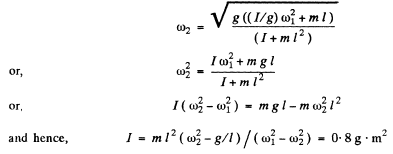
Q.50. Two physical pendulums perform small oscillations about the same horiiontal axis with frequencies ω1 and ω2. Their moments of inertia relative to the given axis are equal to I1 and I2 respectively. In a state of stable equilibrium the pendulums were fastened rigidly together. What will be the frequency of small oscillations of the compound pendulum?
Ans.
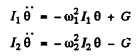
where ± G is the to rque of mutual in teractions. We have written the restoring forces on each pendulum in the absence of the other as 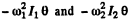 respectively . Then
respectively . Then

Hence 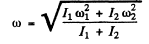
FAQs on Irodov Solutions: Mechanical Oscillations- 4 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are mechanical oscillations? |  |
| 2. How are mechanical oscillations described mathematically? |  |
| 3. What is the relationship between frequency and period in mechanical oscillations? |  |
| 4. What is the concept of resonance in mechanical oscillations? |  |
| 5. How can mechanical oscillations be damped? |  |


















