Irodov Solutions: Mechanical Oscillations- 5 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.51. A uniform rod of length 1 performs small oscillations about the horizontal axis 00' perpendicular to the rod and passing through one of its points. Find the distance between the centre of inertia of the rod and the axis 00' at which the oscillation period is the shortest. What is it equal to?
Ans. Let us locate the rod when it is at small angular position 6 relative to its equilibrium position. If a be the sought distance, the n from the conservation of mechanical energy of oscillation
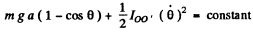
Differentiating w.r.t= time we get :
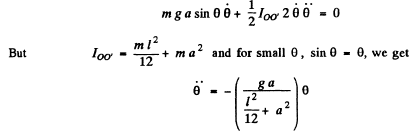
Hence the time period of one full osscillation becomes
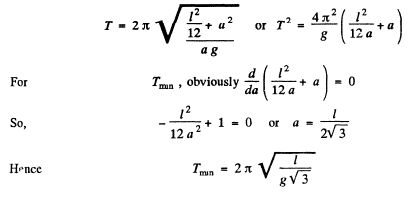
Q.52. A thin uniform plate shaped as an equilateral triangle with a height h performs small oscillations about the horizontal axis coinciding with one of its sides. Find the oscillation period and the reduced length of the given pendulum.
Ans. Consider the moment of inertia of the triangular plate about AB.
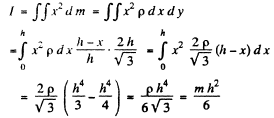
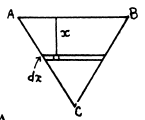
On using the area of the triangle 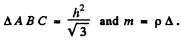
Thus K.E. 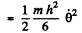
P.E.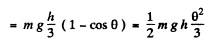
Here 6 is the angle that the instantaneous plane of the plate makes with the equilibrium position which is vertical. (The plate rotates as a rigid body)


Q.53. A smooth horizontal disc rotates about the vertical axis 0 (Fig. 4.15) with a constant angular velocity ω. A thin uniform rod AB of length 1 performs small oscillations about the vertical axis A fixed to the disc at a distance a from the axis of the disc. Find the frequency ωo of these oscillations.
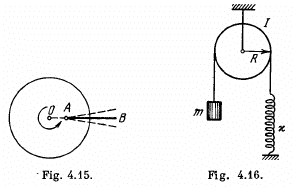
Ans. Let us go to the rotating frame, in which the disc is stationary. In this frame die rod is subjected to coriolis and centrifugal forces, 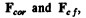 where
where
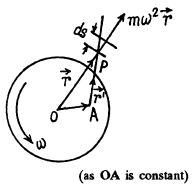
where r is the position of an elemental mass of the rod (Fig.) with respect to point O (disc’s centre) and
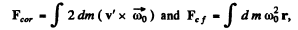

As the rod is vibrating transversely, so v' is directed perpendicular to the length of the rod.
Hence 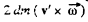 for each elemental mass o f the rod is directed along PA. Therefore the net torque of coriolis about A becomes zero. The not torque of centrifulgal force about point A :
for each elemental mass o f the rod is directed along PA. Therefore the net torque of coriolis about A becomes zero. The not torque of centrifulgal force about point A :
Now, 
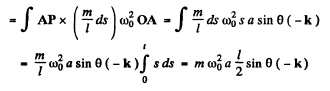
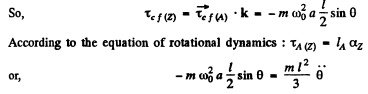

Q.54. Find the frequency of small oscillations of the arrangement illustrated in Fig. 4.16. The radius of the pulley is R, its moment of inertia relative to the rotation axis is I, the mass of the body is m, and the spring stiffness is x. The mass of the thread and the spring is negligible, the thread does not slide over the pulley, there is no friction in the axis of the pulley.
Ans. The physical system consists with a pulley and the block. Choosing an intertial frame, let us direct the x-axis as shown in the figure.
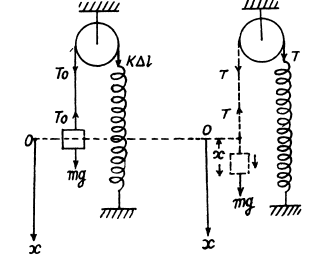
Initially the system is in equilibrium position. Now from the condition of translation equilibrium for the block
To = ms (1)
Similarly for the rotational equilibrium of the pulley
k Δ/R = T0R
or. T0 = k Δ l (2)
from Eqns. (1) and (2)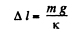 (3)
(3)
Now let us disturb the equilibrium of the system no matter in which way to analyse its motion. At an arbitrary position shown in the figure, from Newton's second law of motion for the block
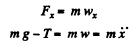 (4)
(4)
Similarly for the pulley
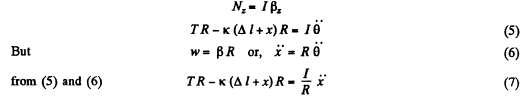
Solving (4) and (7) using the initial condition of the problem
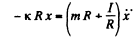
or, 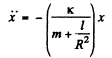
Hence the sought time period, 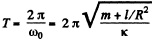
Note : we may solve this problem by using die conservation of mechanical energy also
Q.55. A uniform cylindrical pulley of mass M and radius R can freely rotate about the horizontal axis 0 (Fig. 4.17). The free end of

a thread tightly wound on the pulley carries a deadweight A. At a certain angle α it counterbalances a point mass in fixed at the rim of the pulley. Find the frequency of small oscillations of the arrangement.
Ans. At the equilbrium position, Noz = 0 ( Net torque about 0)
So,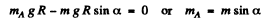 (1)
(1)
From the equation of rotational dynamics of a solid body about the stationary axis (say 2 -axis) of rotation i.e. from Nz = Iβz
when the pulley is rotated by the small angular displacement 0 in clockwise sense relative to the equilibrium position (Fig.), we get :
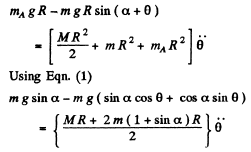
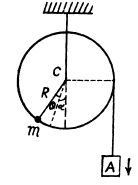
But for small θ, we may write cos θ = 1 and sin θ = θ
Thus we have
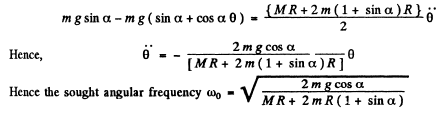
Q.56. A solid uniform cylinder of radius r rolls without sliding along the inside surface of a cylinder of radius R, performing small oscillations. Find their period.
Ans. Let us locate solid cylinder when it is displaced from its stable equilibrium position by the small angle θ during its oscillations (Fig.). If Vc be the instantaneous speed of the C.M. (C) of the solid cylinder which is in pure rolling, then its angular velocity about its own centre C is
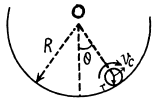
ω = vc/r (1)
Since C moves in a circle of radius (R - r), the speed of C at the same m oment can be written as
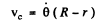 (2)
(2)
Thus from Eqns (1) and (2)
 (3)
(3)
As the mechanical energy of oscillation of the solid cylinder is conserved, i.e. E = T + U = constant
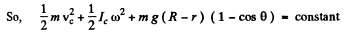
(Where m is the mass of solid cylinder and Ic is the moment of inertia o f the solid cylinder about an axis passing through its C .M . ( C ) and perpendicular to the plane of Fig . of solid cylinder)
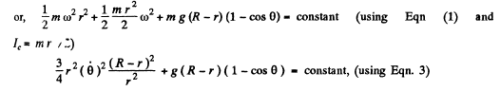
Differentiating w.r.t time
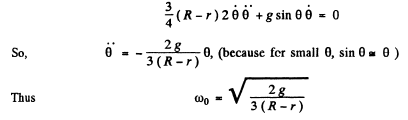
Hence the sought time period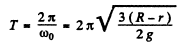
Q.57. A solid uniform cylinder of plass m performs small oscillations due to the action of two springs whose combined stiffness is equal to x (Fig. 4.18). Find the period of these oscillations in the absence of sliding.
Ans. Let k1 and k2 be the spring constant o f left and right sides springs. As the rolling o f th< solid cylinder is pure its lowest point becomes the instanteneous centre of rotation. If θ b( the small angular displacement of its upper most point relative to its equilibrium position, the deformation o f each spring becomes (IR Q) . Since the mechanical energy o f oscillation of the solid cylinder is conserved, E = T+ U = constant
i.e. 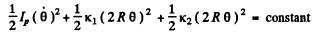
Differentiating w.r.t time
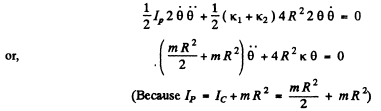
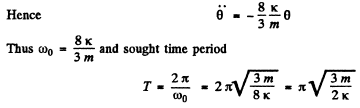
Q.58. Two cubes with masses m1 a nd m2 were interconnected by a weightless spring of stiffness x and placed on a smooth horizontal surface. Then the cubes were drawn closer to each other and released simultaneously. Find the natural oscillation frequency of the system.
Ans. In the C.M. frame (which is rigidly attached with the centre of mass of the two cubes) the cubes oscillates. We know that the kinetic energy of two body system equals 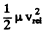 , where p. is the reduced mass and is the modulus of velocity of any one body particle relative to other. From the conservation of mechanical energy of oscillation :
, where p. is the reduced mass and is the modulus of velocity of any one body particle relative to other. From the conservation of mechanical energy of oscillation :
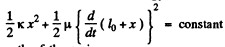
Here l0 is the natural length of the spring.
Differenting the above equation w.r.t time, we get :
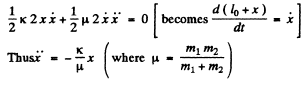
Hence the natural frequency of oscillation :
Q.59. Two balls with masses m1 = 1.0 kg and m2 = 2.0 kg are slipped on a thin smooth horizontal rod (Fig. 4.19). The balls are
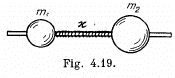
interconnected by a light spring of stiffness x = 24 N/m. The lefthand ball is imparted the initial velocity v1 = 12 cm/s. Find:
(a) the oscillation frequency of the system in the process of motion;
(b) the energy and the amplitude of oscillations.
Ans. Suppose the balls 1 & 2 are displaced by x1, x2 from their initial position. Then the eneigy is
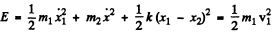
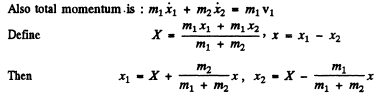
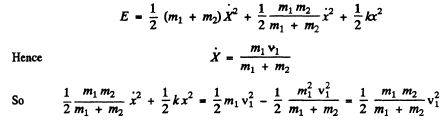
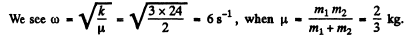
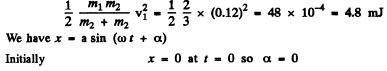
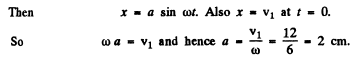
Q.60. Find the period of small torsional oscillations of a system consisting of two discs slipped on a thin rod with torsional coefficient k. The moments of inertia of the discs relative to the rod's axis are equal to I1 and l2.
Ans. Suppose the disc 1 rotates by angle θ1 and the disc 2 by angle θ2 in the opposite sense. Then total torsion of the rod = 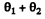
and torsional P.E. 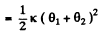
The KJE. of the system (neglecting the moment of inertia of the rod) is
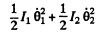
So total eneigy of the rod
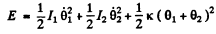
We can put the total angular momentum of the rod equal to zero since the frequency associated with the rigid rotation of the whole system must be zero (and is known).
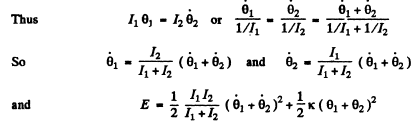
The angular oscillation, frequency corresponding to this is
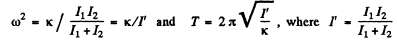
Q.61. A mock-up of a CO2 molecule consists of three balls interconnected by identical light springs and placed along a straight line in the state of equilibrium. Such a system can freely perform oscillations of two types, as shown by the arrows in Fig. 4.20. Knowing the masses of the atoms, find the ratio of frequencies of these oscillations.
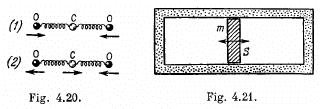
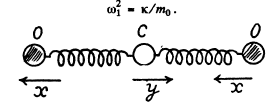
Ans. In the first mode the carbon atom remains fixed and the oxygen atoms move in equal & opposite steps. Then total energy is
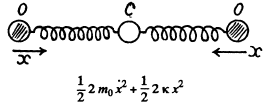
where x is the displacement of one of the 0 atom (say left one). Thus
In this mode the oxygen atoms move in equal steps in the same direction but the carbon atom moves in such a way as to keep the centre of mass fixed.
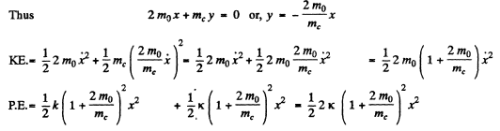
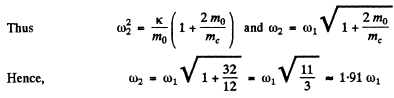
Q.62. In a cylinder filled up with ideal gas and closed from both ends there is a piston of mass m, and cross-sectional area S (Fig. 4.21).
In equilibrium the piston divides the cylinder into two equal parts, each with volume Vo. The gas pressure is Po. The piston was slighlty displaced from the equilibrium position and released. Find its oscillation frequency, assuming the processes in the gas to be adiabatic and the friction negligible.
Ans. Let, us displace the piston through small distance x, towards right, then from Fx = mwx
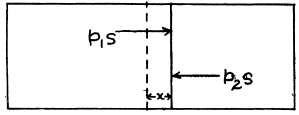
or,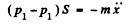 (1)
(1)
But, the process is adiabatic, so from 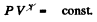
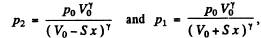
as the new volumes of the left and the right parts are now (Vo + Sx) and (Vo - Sx) respectively.
So, the Eqn (1) becomes.
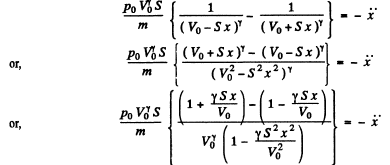
Neglecting the term 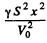 in the denominator, as it is very sm all, we get
in the denominator, as it is very sm all, we get
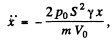
which is the equation for S.H.M. and hence the oscillating frequency.
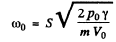
Q.63. A small ball of mass m = 21 g suspended by an insulating thread at a height h = 12 cm from a large horizontal conducting plane performs small oscillations (Fig. 4.22). After a charge q had been imparted to the ball, the oscillation period changed η = 2.0 times. Find q.
Ans. In the absence of the charge, the oscillation period of the ball
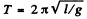
when we impart the charge q to the ball, it will be influenced by the induced charges on the conducting plane. From the electric image method the electric force on the ball by the plane  and is directed downward . Thus in this case the effective acceleration of the ball
and is directed downward . Thus in this case the effective acceleration of the ball
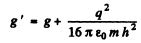
and the corresponding time period
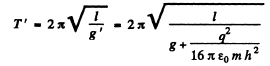
From the conditon of the problem
Thus on solving
Q.64. A small magnetic needle performs small oscillations about an axis perpendicular to the magnetic induction vector. On changing the magnetic induction the needle's oscillation period decreased η = 5.0 times. How much and in what way was the magnetic induction changed? The oscillation damping is assumed to be negligible.
Ans. In a magnetic field of induction B the couple on the magnet is - MB sinθ = - MBθ equating this to  we get
we get
The induction of the field increased η2 times.
Q.65. A loop (Fig. 4.23) is formed by two parallel conductors connected by a solenoid with inductance L and a conducting rod of mass m which can freely (without friction) slide over the conductors. The conductors are located in a horizontal plane in a uniform vertical magnetic field with induction B. The distance between the conductors is equal to 1. At the moment t = 0 the rod is imparted an initial velocity vo directed to the right. Find the law of its motion x (t) if the electric resistance of the loop is negligible.
Ans. We have in the circuit at a certain instant of time (t), from Faraday’s law of electromagnetic induction :

For the rod from the second law of motion Fx = mwx
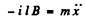
Using Eqn. (I), we get :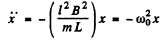 (2)
(2)
where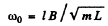
The solution of the above differential equation is of the form
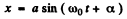
From the initial condition, at = 0 , x = 0 , so α = 0
Hence,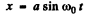 (3)
(3)
Differentiating w.r.t time, 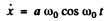
But from the initial condition of the problem at 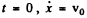
Thus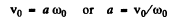 (4)
(4)
Putting the value of a from Eqn. (4) into Eqn. (3), we obtained
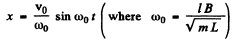
FAQs on Irodov Solutions: Mechanical Oscillations- 5 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are mechanical oscillations? |  |
| 2. How are mechanical oscillations described mathematically? |  |
| 3. What is the relationship between frequency and period in mechanical oscillations? |  |
| 4. What is resonance in mechanical oscillations? |  |
| 5. How is damping related to mechanical oscillations? |  |


















