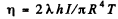Irodov Solutions: Mechanical Oscillations- 6 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download

Q.66. A coil of inductance L connects the upper ends of two vertical copper bars separated by a distance l. A horizontal conducting connector of mass m starts falling with zero initial velocity along the bars without losing contact with them. The whole system is located in a uniform magnetic field with induction B perpendicular to the plane of the bars. Find the law of motion x (t) of the connector. 

Ans. As the connector moves, an emf is set up in the circuit and a current flows, since the emf is

provided x is measured from the initial position.

We then have

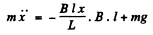
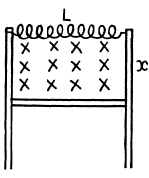
for by Lenz’s law the induced current will oppose downward sliding. Finally

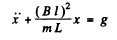
on putting

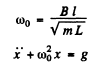
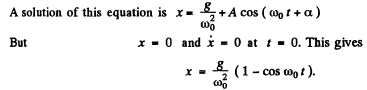
Q.67. A point performs damped oscillations according to the law 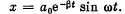 Find: (a) the oscillation amplitude and the velocity of the point at the moment t = 0; (b) the moments of time at which the point reaches the extreme positions. 

Ans. We are given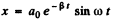 

(a) The velocity of the point at t = 0 is obtained from

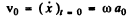
The term "oscillation amplitude at the moment t = 0" is meaningless. Probably the implication is the amplitude for  sin ωt and amplitude is a_o.

(b)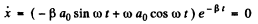 

when the displacement is an extremum. Then

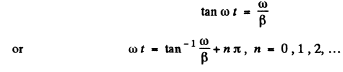
Q.68. A body performs torsional oscillations according to the law 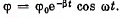 Find: 

(a) the angular velocity 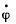 and the angular acceleration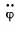of the body at the moment t = 0; (b) the moments of time at which the angular velocity becomes maximum. 

Ans. 

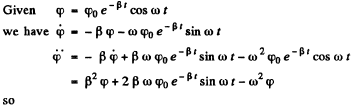
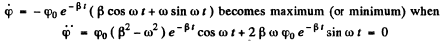
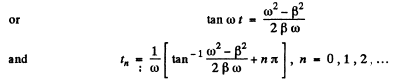
Q.69. A point performs damped oscillations with frequency ω and damping coefficient   according to the law (4.1b). Find the initial amplitude a, and the initial phase a if at the moment t = 0 the displacement of the point and its velocity projection are equal to

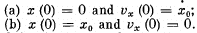
Ans. 

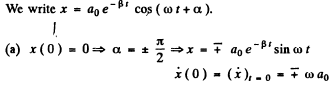
 Since a0 is + ve, we must choose the upper sign if  and the lower sign if

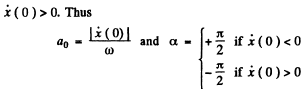
(b) 

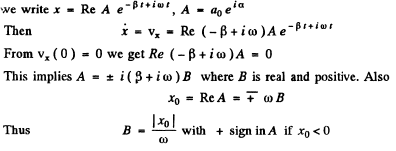
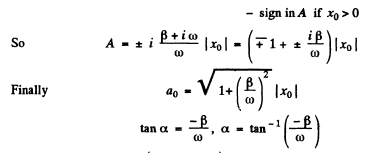
Q.70. A point performs damped oscillations with frequency ω = = 25 s^-1. Find the damping coefficient l if at the initial moment the velocity of the point is equal to zero and its displacement from the equilibrium position is η = 1.020 times less than the amplitude at that moment. 

Ans.

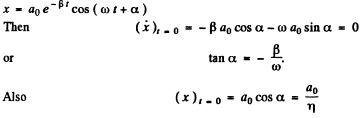
Q.71. A point performs damped oscillations with frequency ω and damping coefficient β. Find the velocity amplitude of the point as a function of time t if at the moment t = 0
 (a) its displacement amplitude is equal to a₀;
 (b) the displacement of the point x (0) = 0 and its velocity pro- jection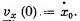 

Ans. 

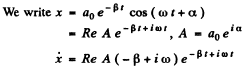
Velocity amplitude as a function of time is defined in the following manner. Put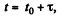 

then

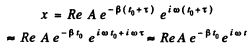
for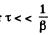 This means that the displacement amplitude around the time  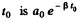and we can say that the displacement amplitude at time  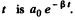Similarly for the velocity amplitude.
Clearly

(a) Velocity amplitude at time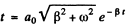  

Since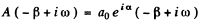  

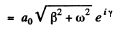
where y is anotner constant

(b)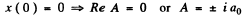  

where a₀ is real and positive.

Also

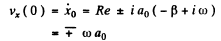
Thus   and we take - ( + ) sign if x₀ is negative (positive). Finally the velocity amplitude is obtained as

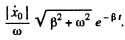
Q.72. There are two damped oscillations with the following periods T and damping coefficients β: T₁ =  0.10 ms, β₁  = 100s^-1  and T₂  = 10ms, β₂  = 10s^-1. Which of them decays faster?

Ans. The first oscillation decays faster in time. But if one takes the natural time scale, the period T for each oscillation, the second oscillation attenuates faster during that period. 

Q.73. A mathematical pendulum oscillates in a medium for which the logarithmic damping decrement is equal to 20  = 1.50. What will be the logarithmic damping decrement if the resistance of the medium increases n = 2.00 times? How many times has the resistance of the medium to be increased for the oscillations to become impossible? 

Ans. By definition of the logarithemic decrement 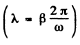we get for the original decrement

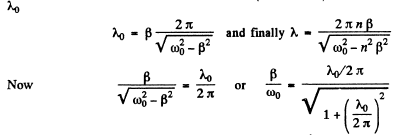
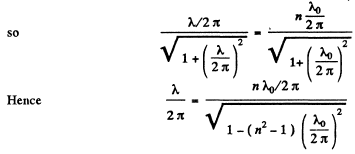
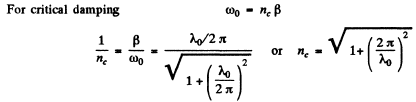
Q.74. A deadweight suspended from a weightless spring extends it by Δx = 9.8 cm. What will be the oscillation period of the dead Weight when it is pushed slightly in the vertical direction? The logarithmic damping decrement is equal to λ = 3.1.  

Ans.  The Eqn of the dead weight is 

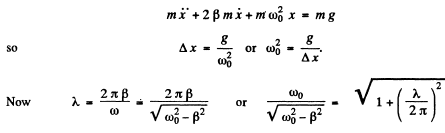
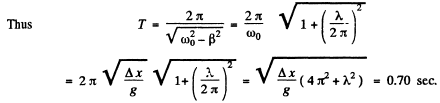
Q.75. Find the quality factor of the oscillator whose displacement amplitude decreases η = 2.0 times every n = 110 oscillations. 

Ans. The displacement amplitude decrease η times every n oscillations. Thus

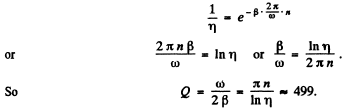
Q.76. A particle was displaced from the equilibrium position by a distance l = 1.0 cm and then left alone. What is the distance that the particle covers in the process of oscillations till the complete stop, if the logarithmic damping decrement is equal to λ = 0.020? 

Ans.

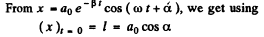
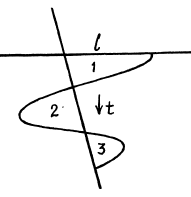
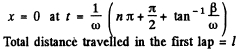
To get the maximum displacement in thfe second lap we note that

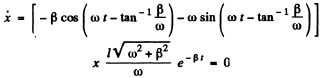
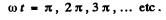
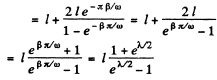
where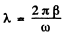, is the logarithemic decrement Substitution gives 2 metres.

Q.77. Find the quality factor of a mathematical pendulum l = = 50 cm long if during the time interval δ = 5.2 min its total mechanical energy decreases η = 4.0.10⁴  times. 

Ans. For an undamped oscillator the mechanical energy 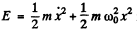is conserved. For a damped oscillator.

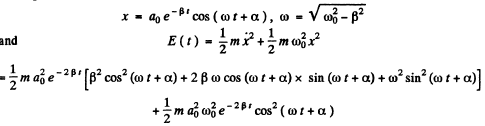
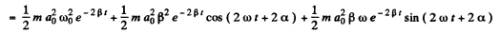
If 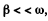 then the average of the last two terms over many oscillations about the time t will vanish and

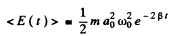
and this is the relevant mechanical energy.

In time δ this decreases by a factor 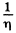so

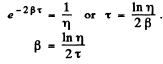
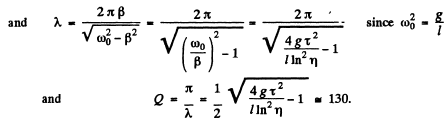
Q.78. A uniform disc of radius R = 13 cm can rotate about a horizontal axis perpendicular to its plane and passing through the edge of the disc. Find the period of small oscillations of that disc if the logarithmic damping decrement is equal to λ = 1.00. 

Ans. The restoring couple is

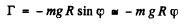
The moment of inertia is

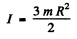
Thus for undamped oscillations

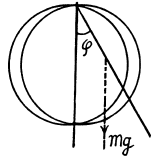
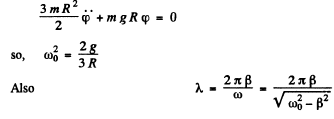
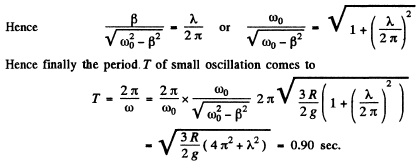
Q.79. A thin uniform disc of mass m and radius R suspended by an elastic thread in the horizontal plane performs torsional oscillations in a liquid. The moment of elastic forces emerging in the thread is equal to N = αφ, where a is a constant and IT is the angle of rotation from the equilibrium position. The resistance force acting on a unit area of the disc is equal to F₁ = ηv, where is a constant and η is the velocity of the given element of the disc relative to the liquid. Find the frequency of small oscillation. 

Ans. Let us calculate the moment G₁ of all the resistive forces on the disc. When the disc rotates an element (rdrdθ) with coordinates (r,θ) has a velocity r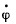, where φ is the instantaneous angle of rotation from the equilibrium position and r is measured from the centre. Then

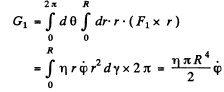
Also moment of inertia =

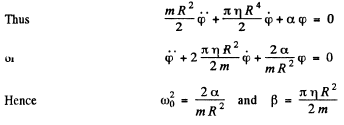
and angular frequency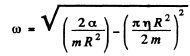 

Note:- normally by frequency we mean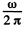 

Q.80. A disc A of radius R suspended by an elastic thread between two stationary planes (Fig. 4.24) performs torsional oscillations about its axis 00'. The moment of inertia of the disc relative to that axis is equal to I, the clearance between the disc and each of the planes is equal to h, with h << R. Find the viscosity of the gas surrounding the disc A if the oscillation period of the disc equals T and the logarithmic damping decrement, λ. 

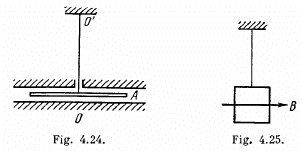
Ans. From the law of viscosity, force per unit area =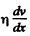 

so when the disc executes torsional oscillations the resistive couple on it is

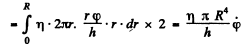
(factor 2 for the two sides of the disc; see the figure  in the book) where φ is torsion. The equation of motion is

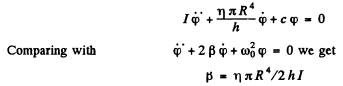
Now the logarithmic decrement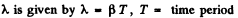 

Thus