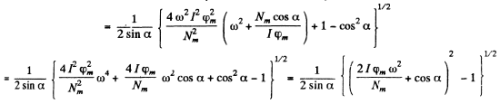Irodov Solutions: Mechanical Oscillations- 7 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download

Q.81. A conductor in the shape of a square frame with side a suspended by an elastic thread is located in a uniform horizontal magnetic field with induction B. In equilibrium the plane of the frame is parallel to the vector B (Fig. 4.25). Having been displaced from the equilibrium position, the frame performs small oscillations about a vertical axis passing through its centre. The moment of inertia of the frame relative to that axis is equal to I, its electric resistance is R. Neglecting the inductance of the frame, find the time interval after which the amplitude of the frame's deviation angle decreases e-fold.

Ans. If φ = angle of deviation of the frame from its normal position, then an e.m.f.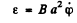

is induced in the frame in the displaced position and a current 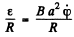 flows in it. A couple

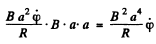
then acts on the frame in addition to any elastic restoring couple c φ. We write the equation of the frame as

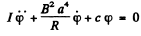
 Thus 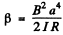 where β is defined in the book.

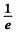Amplitude of oscillation die out according to  so time required for the oscillations to decrease to of its value is 

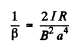
Q.82. A bar of mass m = 0.50 kg lying on a horizontal plane with a friction coefficient k = 0.10 is attached to the wall by means of a horizontal non-deformed spring. The stiffness of the spring is equal to x = 2.45 N/cm, its mass is negligible. The bar was displaced so that the spring was stretched by x₀ = 3.0 cm, and then released. Find:
 (a) the period of oscillation of the bar;
 (b) the total number of oscillations that the bar performs until it stops completely.

Ans. We shall denote the stiffness constant by k . Suppose the spring is stretched by x₀ . The bar in then subject to two horizontal forces (1) restorin g force - k x and (2) friction kmg opposing motion. If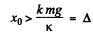  

 the bar will come back.

(If x₀ ≤ Δ , the bar will stay put) The equation of the bar when it is moving to the left is

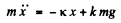
This equation has the solution

where we have used 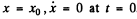 This solution is only valid till the bar comes to rest. This happens at

and at that time 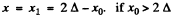   the tendency of the rod will now be to move to the right . (if  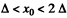the rod will stay put now) Now the equation for rightward motion becomes'*

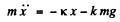
(the friction force has reversed ).

We notice that the rod will move to the right only if

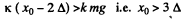
In this case the solution is

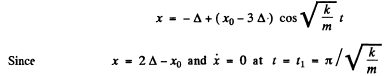
The rod will next come to rest at

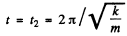
and at that instant 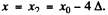. How ever the rod will stay put unless x₀ > 5Δ. Thus

(a) time period of one full oscillation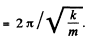   

(b) There is no oscillation if 0 < x₀ < Δ     

One half oscillation if Δ < x₀ < 3Δ

2 half oscillation if 3Δ < x₀< 5Δ etc.
We can say that the number of full oscillations is one half of the integer n

where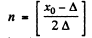

where [ x ] = smallest non-negative integer greater than x.

Q.83. A ball of mass m can perform undamped harmonic oscillations about the point x = 0 with natural frequency ω_o. At the moment t = 0, when the ball was in equilibrium, a force F_x = F₀  cos ωt coinciding with the x axis was applied to it. Find the law of forced oscillation x (t) for that ball. 

Ans. The equation of motion of the ball is

.

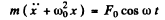This equation has the solution

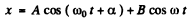
where A and a are arbitrary and B is obtained by substitution in the above equation

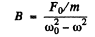
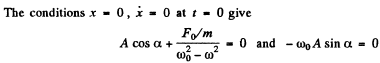
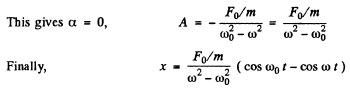
Q.84. A particle of mass m can perform undamped harmonic oscillations due to an electric force with coefficient k. When the particle was in equilibrium, a permanent force F was applied to it for δ seconds. Find the oscillation amplitude that the particle acquired after the action of the force ceased. Draw the approximate plot x (t) of oscillations. Investigate possible cases.

Ans. We have to look for solutions of the equation

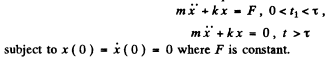
The solution of this equation will be sought in the form

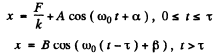
 A and α will be determined from the boundary condition at t = 0.

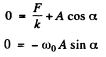
Thus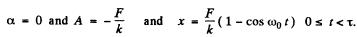 

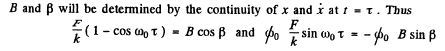
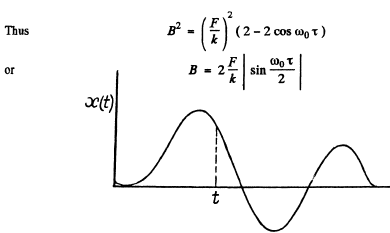
Q.85. A ball of mass m, when suspended by a spring stretches the latter by Δl. Due to external vertical force varying according to a harmonic law with amplitude F₀  the ball performs forced oscillations. The logarithmic damping decrement is equal to λ. Neglecting the mass of the spring, find the angular frequency of the external force at which the displacement amplitude of the ball is maximum. What is the magnitude of that amplitude? 

Ans. Foi the spring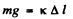

 where k is its stifiiess coefficient. Thus

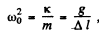
The equation of motion of the ball is

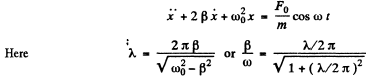
To find the solution of the above equation we look for the solution of the auxiliary equation

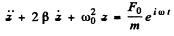
Clearly we can take 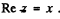 Now we look for a particular integral for z of the form

Thus, substitution gives A and we get

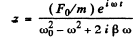
so taking the real part

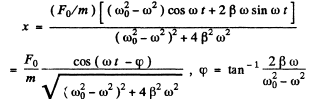
The amplitude of this oscillation is maximum when the denominator is minimum. Tthis happens when

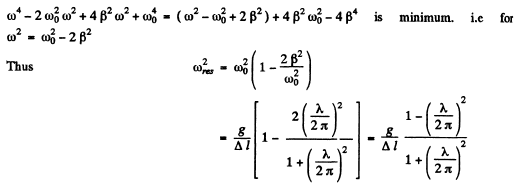
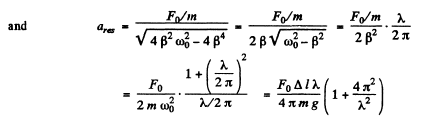
Q.86. The forced harmonic oscillations have equal displacement amplitudes at frequencies ω₁ = 400 s^-1  and ω₂ = 600s^-1 . Find the resonance frequency at which the displacement amplitude is maximum. 

Ans.

Q.87. The velocity amplitude of a particle is equal to half the maximum value at the frequencies ω₁  and ω₂ of external harmonic force. Find:
 (a) the frequency corresponding to the velocity resonance;
 (b) the damping coefficient β and the damped oscillation frequency co of the particle. 

Ans.

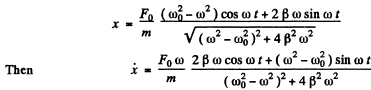
Thus the velocity amplitude is

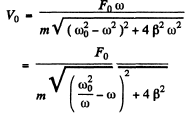
This is maximum when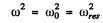

and then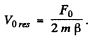 

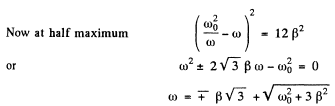
 where we have rejected a solution with - ve sign before there dical. Writing

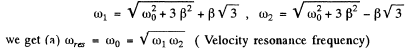
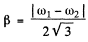and damped oscillation frequency

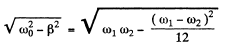
Q.88. A certain resonance curve describes a mechanical oscillating system with logarithmic damping decrement λ = 1.60. For this curve find the ratio of the maximum displacement amplitude to the displacement amplitude at a very low frequency. 

Ans. In general for displacement amplitude

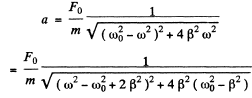
Hence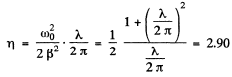

Q.89. Due to the external vertical force F_x  = F₀  cos ωt a body suspended by a spring performs forced steady-state oscillations according to the law x = a cos (ωt — φ). Find the work performed by the force F during one oscillation period. 

Ans. The work done in one cycle is

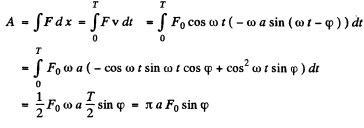
Q.90. A ball of mass m = 50 g is suspended by a weightless spring with stiffness x = 20.0 N/m. Due to external vertical harmonic force with frequency ω = 25.0 s^-1  the ball performs steady-state oscillations with amplitude a = 1.3 cm. In this case the displace- ment of the ball lags in phase behind the external force by

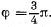
Find: (a) the quality factor of the given oscillator; (b) the work performed by the external force during one oscillation period. 

Ans. In the formula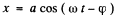 

we have

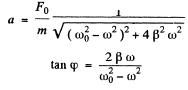
Thus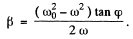  

Hence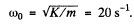 

and (a) the quality factor

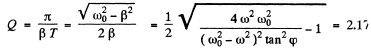
 (b) work done is 

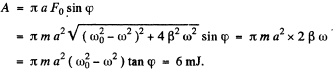
Q.91. A ball of mass m suspended by a weightless spring can perform vertical oscillations with damping coefficient β. The natural oscillation frequency is equal to ω₀. Due to the external vertical force varying as F_x = F_o , cos ωt the ball performs steady-state harmonic oscillations. Find:
 (a) the mean power (P), developed by the force F, averaged over one oscillation period;
 (b) the frequency ω of the force F at which (P) is maximum; what is (P)_max equal to? 

Ans. Here as usual 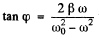  where φ is the phase lag of the displacement

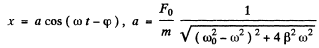
(a) Mean power developed by the force over one oscillation period

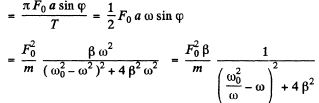
(b) Mean power < P > is maximum when ω = ω₀ (for the denominator is then minimuir Also

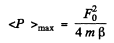
Q.92. An external harmonic force F whose frequency can be varied, with amplitude maintained constant, acts in a vertical direction on a ball suspended by a weightless spring. The damping coefficient is times less than the natural oscillation frequency ω_o of the ball. How much, in per cent, does the mean power (P) developed by the force F at the frequency of displacement resonance differ from the maximum mean power (P)_max?  Averaging is performed over one oscillation period. 

Ans. Given Then from the previous problem

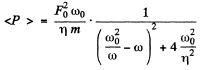
At displacement resonance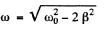 

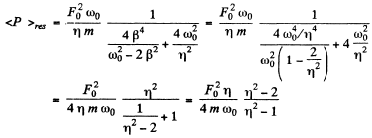
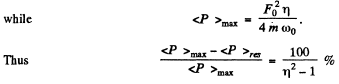
Q.93. A uniform horizontal disc fixed at its centre to an elastic vertical rod performs forced torsional oscillations due to the moment of forces 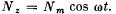 The oscillations obey the law φ  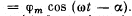Find: (a) the work performed by friction forces acting on the disc during one oscillation period; (b) the quality factor of the given oscillator if the moment of inertia of the disc relative to the axis is equal to I. 

Ans. The equation of the disc is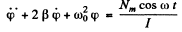

Then as before

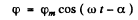
where

 (a) Work performed by frictional forces

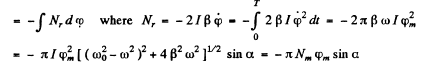
(b) The quality factor