Irodov Solutions: Molecules and Crystals- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download

Q.186. Calculate the Debye temperature for iron in which the propagation velocities of longitudinal and transverse vibrations are equal to 5.85 and 3.23 km/s respectively.

Ans. We proceed as in the previous example. The total number of modes must be 3n₀ v (total transverse and one longitudinal per atom). On the other hand the number of transverse modes per unit frequency interval is given by

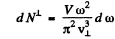
.while the number of longitudinal modes per unit frequency tnterval is given by

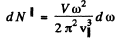
The total number per unit frequency interval is

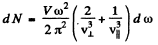
If the high frequency cut off is at 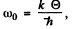the total number of modes will be

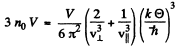
Here n₀ is the number of iron atoms per unit volume. Thus

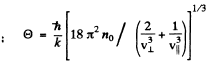
For iron

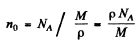
(p = density, M = atomic weight of iron N_A = Avogadro number).

n_o = 8.389 x 10²² per cc

Substituting the data we get

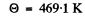
Q.187. Evaluate the propagation velocity of acoustic vibrations in aluminium whose Debye temperature is 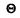 = 396 K.

Ans. We apply the same formula but assume 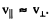   Then

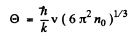
or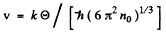 

For Al

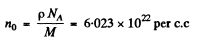
Thus                v = 3.39 km/s .

The tabulated values are  

and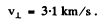 

Q.188. Derive the formula expressing molar heat capacity of a unidimensional crystal, a chain of identical atoms, as a function of temperature T if the Debye temperature of the chain is equal to 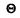. Simplify the obtained expression for the case T >> .

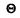Ans. In the Debye approximation the number of modes per unit frequency interval is given by

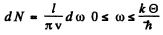
But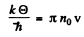 

Thus 

The energy per mode is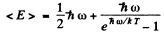 

Then the total interval energy of the chain is

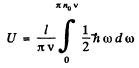
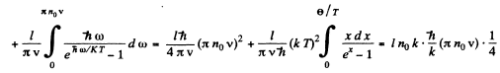
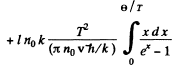
We put ln₀ it = for 1 mole of the chain.

Then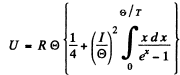 

Hence the molar heat capacity is by differentiation

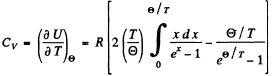
when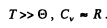 

Q.189. In a chain of identical atoms the vibration frequency ω depends on wave number k as ω = ω_max  sin (ka/2), where ω_max is the maximum vibration frequency, k = 2π/λ is the wave number corresponding to frequency ω, a is the distance between neighbouring atoms. Making use of this dispersion relation, find the dependence of the number of longitudinal vibrations per unit frequency interval on ω, i.e. dN/dω, if the length of the chain is l Having obtained dN/dω, find the total number N of possible longitudinal vibrations of the chain. 

Ans. If the chain has N atoms, we can assume atom number 0 and N +1 held ficed. Then the displacement of the n^th atom has the form

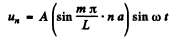
Here 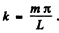 Allowed frequencies then have the form 

In our form only +ve k values are allowed.

The number of modes in a wave number range dk is

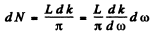
 But

Hence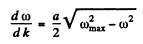 

So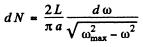  

(b) The total number of modes is

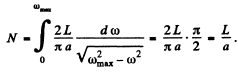
i.e. the number of atoms in the chain.

Q.190. Calculate the zero-point energy per one gram of copper whose Debye temperature is 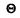 = 330 K. 

Ans. Molar zero point energy is 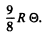The zero point energy per gm of copper is  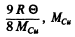is the atomic weight of the copper.
Substitution gives 48-6 J / g m .

Q.191. Fig. 6.10 shows heat capacity of a crystal vs temperature in terms of the Debye theory. Here C_cl is classical heat capacity, 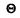 is the Debye temperature. Using this plot, find: 

(a) the Debye temperature for silver if at a temperature T = 65 K its molar heat capacity is equal to 15 J/(mol•K);
 (b) the molar heat capacity of aluminium at T = 80 K if at T = 250 K it is equal to 22.4 J/(mol•K);
 (c) the maximum vibration frequency for copper whose heat capacity at T = 125 K differs from the classical value by 25%

Ans. (a) By Dulong and Petit's law, the classical heat capacity is 3 R - 24-94 J/K - mole. Thus

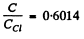
From the graph we see that this

value of 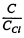 corresponds to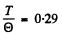 

Hence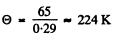 

 (b) 22.4 J/mole - K corresponds to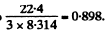 From the graph this corresponds to

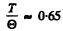 This gives

Then 80 K corresponds to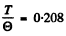 

The corresponding value of 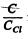is 0.42. Hence C = 10.5 J/mole - K .

(c) We calculate © from the datum tha 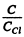 = 0.75 at T = 125 K .

The x-coordinate corresponding to 0.75 is 0.40. Hence

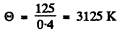
 Now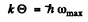      

So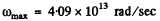  

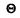Q.192. Demonstrate that molar heat capacity of a crystal at a temperature T << , where  is the Debye temperature, is defined by Eq. (6.4f). 

Ans. We use the formula (6.4d)

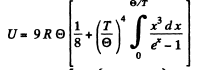
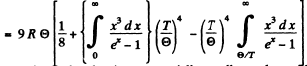
In the limit 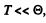 the third term in the bracket is exponentially small together wil derivatives.
Then we can drop the last term

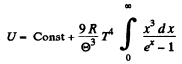
 Thus

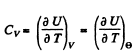
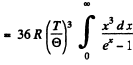
Now from the table in the book

Thus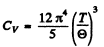 

Note Call the 3^rd term in the bracket above - U₃ Then

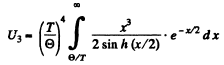
The maximum value of 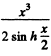  is a finite + v e quantity C₀ for 0 ≤ x <  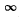Thus

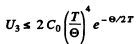
we see that U₃ is exponentially small as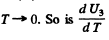  

Q.193. Can one consider the temperatures 20 and 30 K as low for a crystal whose heat capacities at these temperatures are equal to 0.226 and 0.760 J/(mol- K)? 

Ans. At low temperatures 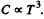. This is also a test of the “ lowness ” of the temperature We see that

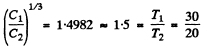
Thus T³ law is obeyed and T₁, T₂ can we regarded low .

Q.194. Calculate the mean zero-point energy per one oscillator of a crystal in terms of the Debye theory if the Debye temperature of the crystal is equal to .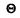 

Ans. The total zero point energy of 1 mole of the solid is 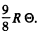Dividing this by the number of modes 3N we get the average zero point energy per mode. It is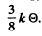 

Q.195. Draw the vibration energy of a crystal as a function of frequency (neglecting the zero-point vibrations). Consider two cases: T = /2 and T = /4, where 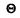 is the Debye temperature.

Ans. In the Debye model

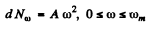
 Then 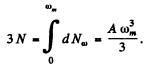      (Total no of modes is 3N) 

Thus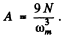  

wc get 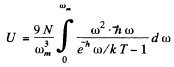   ignoring zero point energy

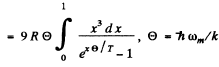
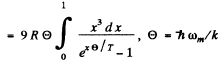
Thus   for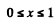 

 For

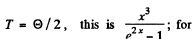
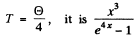Plotting then we get the figures given in the answer.

Q.196. Evaluate the maximum values of energy and momentum of a phonon (acoustie quantum) in copper whose Debye temperature is equal to 330 K.

Ans. The maximum energy of the phonon is

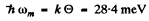
On substituting 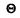 - 330 K .

To get the corresponding value of the maximum momentum we must know the dispersion relation 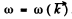 . For small  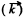we know  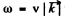where v is velocity o f sound in the crystal. For an order of magnitude estimate we continue to use this result for high  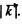Then we estimate v from the values of the modulus of elasticity and density

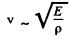
We write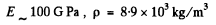  

Then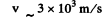 

Hence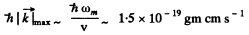  

Q.197. Employing Eq. (6.4g), find at T = 0:
 (a) the maximum kinetic energy of free electrons in a metal if their concentration is equal to n;
 (b) the mean kinetic energy of free electrons if their maximum kinetic energy T_max  is known. 

Ans. (a) From the formula

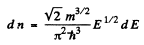
the maximum value E_max of E is determined in terms of n by

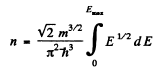
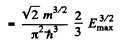
or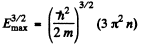           

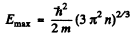
(b) Mean K.E. < E >is

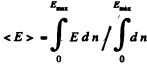
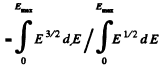
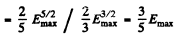
Q.198. What fraction (in per cent) of free electrons in a metal at T = 0 has a kinetic energy exceeding half the maximum energy? 

Ans. The fraction is

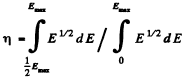
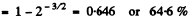
Q.199. Find the number of free electrons per one sodium atom at T = 0 if the Fermi level is equal to E_F = 3.07 eV and the density of sodium is 0.97 g/cm³. 

Ans. We calculate the concentration n of electron in the Na metal from

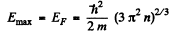
we get from

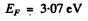
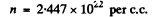
From this we get the number of electrons per one Na atom as

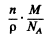
where p = density of Na, M = molar weight in gm of Na, N_A = Avogadro number 

we get

0.963 elecrons per one Na atom.

Q.200. Up to what temperature has one to heat classical electronic gas to make the mean energy of its electrons equal to that of free electrons in copper at T = 0? Only one free electron is supposed to correspond to each copper atom. 

Ans. The mean K.E. of electrons in a Fermi gas is 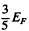. This must equal  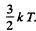Thus

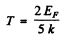
 We calculate E_F first For Cu

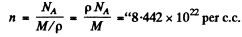
Then E_{F =} 7.01 eV 

and T = 3 -2 5 x 10⁴ K