Irodov Solutions: Nuclear Reactions- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.249. An alpha-particle with kinetic energy Tα =7 .0 MeV is scattered elastically by an initially stationary Li6 nucleus. Find the kinetic energy of the recoil nucleus if the angle of divergence of the two particles is 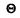 = 60°.
= 60°.
Ans. Initial momentum of the a particle is  is a unit vector in the incident direction). Final momenta are respectively
is a unit vector in the incident direction). Final momenta are respectively  Conservation of momentum reads
Conservation of momentum reads
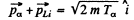
Squaring 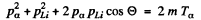 (1)
(1)
where 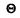 is the angle between
is the angle between 
Also by energy conservation 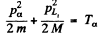
(m & M are respectively the masses of a particle and 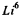 ) So
) So
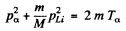 (2)
(2)
Substracting (2) from (1) we see that
Thus if 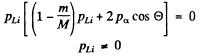
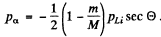
Since pα, pLi are both positive number (being magnitudes of vectors) we must have
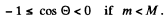
This being understood, we write
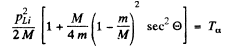
Hence the recoil energy of the Li, nucleus is
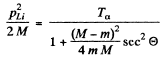
As we pointed out above 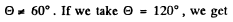 recoil energy of Li = 6 MeV
recoil energy of Li = 6 MeV
Q.250. A neutron collides elastically with an initially stationary deuteron. Find the fraction of the kinetic energy lost by the neutron (a) in a head-on collision; (b) in scattering at right angles.
Ans. (a) In a head on collision
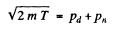
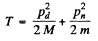
Where pd and pn are the momenta of deuteron and neutron after the collision. Squaring
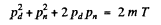
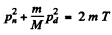
or since pd = 0 in a head on collisions
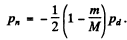
Going back to energy conservation
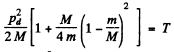
So 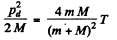
This is the energy lost by neutron. So the fraction of energy lost is
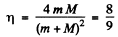
(b) In this case neutron is scattered by 90°. Then we have from the diagram
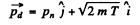
Then by eneigy conservation
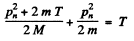
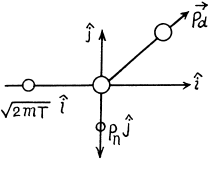
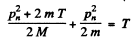
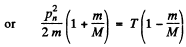
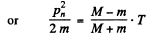
The energy lost by neutron in then
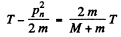
or fraction of energy lost is 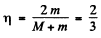
6.251. Find the greatest possible angle through which a deuteron is scattered as a result of elastic collision with an initially stationary proton.
Ans. From conservation of momentum
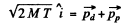
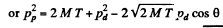
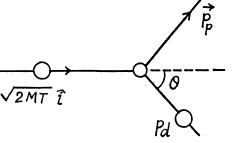
From energy conservation
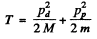
(M = mass of denteron, m = mass of proton)
So 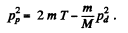
Hence 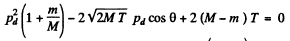
For real roots 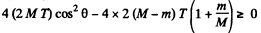
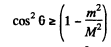
Hence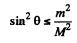
i.e.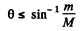
For deuteron-proton scaltering 
6.252. Assuming the radius of a nucleus to be equal to 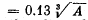 pm, where A is its mass number, evaluate the density of nuclei and the number of nucleons per unit volume of the nucleus.
pm, where A is its mass number, evaluate the density of nuclei and the number of nucleons per unit volume of the nucleus.
Ans. This problem has a misprint Actually the radius R of a nucleus is given by
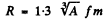
where 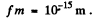
Then the number of nucleous per unit volume is 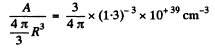
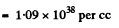
The corresponding mass density is (1.09 x 10-38 x mass of a nucleon) per cc = 1.82 x 1011kg/cc
6.253. Write missing symbols, denoted by x, in the following nuclear reactions: (a) B10 (x, α) Be8
(b) O17 (d, n) x; (c) Na23 (p, x) Ne20; (d) x (p, n) Ar37.
Ans. (a) The particle x must carry two nucleons and a unit of positive charge.
The reaction is
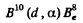
(b) The particle x must contain a proton in addition to the constituents of O17. Thus the reaction is
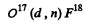
(c) The particle x must carry nucleon number 4 and two units of +ve charge. Thus the particle must be x = α and the reaction is
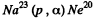
(d) The particle x must carry mass number 37 and have one unit less of positive charge.
Thus x = Cl 37 and the reaction is
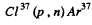
6.254. Demonstrate that the binding energy of a nucleus with mass number A and charge Z can be found from Eq. (6.6b).
Ans. From the basic formula
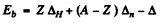
We define
AH = mH - 1 amu
An = - 1 amu
A = M - A amu
Then clearly Eb - Z A# + (A - Z ) An - A
6.255. Find the binding energy of a nucleus consisting of equal numbers of protons and neutrons and having the radius one and a half times smaller than that of A127 nucleus.
Ans. The mass number of the given nucleus must be
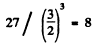
Thus the nucleus is Be8. Then Ihe binding eneigy is
E b - 4 x 0-00867 + 4 + x 0-00783 - 0-00531 amu
= 0-06069 amu = 56-5 MeV
On using 1 amu = 931 MeV.
6.256. Making use of the tables of atomic masses, find: (a) the mean binding energy per one nucleon in O16 nucleus; (b) the binding energy of a neutron and an alpha-particle in a B11 nucleus; (c) the energy required for separation of an O16 nucleus into four identical particles.
Ans. (a) Total binding eneigy of Ihe O16 nucleus is
Eb = 8 x .00867 + 8 x .00783 + 0.00509 amu
= 0.13709 amu = 127.6 MeV
So B.E. per nucleon is 7.98 Mev/nucleon
(b) B.E. of neutron in B11 nucleus
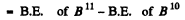
(since on removing a neutron from B11 we get B10)

= 0.01231 amu = 11.46 MeV
B.E. of ( an α-particle in B11)
= B.E. of B1 - B.E. of Li7 - B.E. of α
(since on removing an a from B11 we get Li7 )
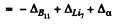
= - 0.00930 + 0.01601 + 0.00260
= 0.00931 amu = 8.67 MeV
(c) This eneigy is
[B.E. of O16 + 4 (B.E. of a particles)]
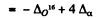
= 4 x 0-00260 + 0.00509
= 0.01549 amu - 14.42 MeV
6.257. Find the difference in binding energies of a neutron and a proton in a B11 nucleus. Explain why there is the difference.
Ans. B.E. o f a neutron in B11 - B.E. of a proton in B11
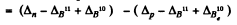
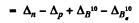 = 0.00867 - 0.00783
= 0.00867 - 0.00783
+ 0.01294 - 0.01354 = 0.00024 amu = 0.223 MeV
The difference in binding energy is essentially due to the coulomb repulsion between the proton and the residual nucleus Be10 which together constitute B11.
6.258. Find the energy required for separation of a Ne20 nucleus into two alpha-particles and a C12 nucleus if it is known that the binding energies per one nucleon in Ne20, He4, and C12 nuclei are equal to 8.03, 7.07, and 7.68 MeV respectively.
Ans. Required energy is simply the difference in total binding energies
= B.E. of Ne20 - 2 (BE. of He4) - B.E. of C12
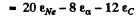
(ε is binding energy per unit nucleon.) Substitution gives 11.88MeV .
6.259. Calculate in atomic mass units the mass of (a) a Li8 atom whose nucleus has the binding energy 41.3 MeV; (b) a C10 nucleus whose binding energy per nucleon is equal to 6.04 MeV.
Ans. We have for 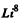
41.3 MeV = 0.044361 amu = 3ΔH + 5Δn - Δ
Hence Δ = 3 x 0.00783 + 5 x 0.00867 - 0.09436 - 0.02248 amu
(b) For C10 10 x 6.04 = 60.4 MeV
- 0-06488 amu
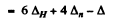
Hence Δ = 6 x 0.00783 + 4 x 0-00867 - 0.06488 = 0.01678 amu
Hence the mass of C10 is 10.01678 amu
6.260. The nuclei involved in the nuclear reaction A1 + A2 → → A3 + A4 have the binding energies E1, E2, E3, and E4. Find the energy of this reaction.
Ans. Suppose M1 , M2 , M3 , M4 are the rest masses of the nuclei A1 lf A2 , A3 and A4 participating in the reaction

Here Q is the energy released. Then by conservation of energy.
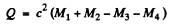
Now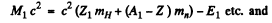
Z1 + Z2 = Z3 + Z4 (conservation of change)
A1 + A2 = A3 + A4 (conservation of heavy particles)
Hence Q = (Es + E4) - (Ex + E2)
6.261. Assuming that the splitting of a U236 nucleus liberates the energy of 200 MeV, find: (a) the energy liberated in the fission of one kilogram of U236 isotope, and the mass of coal with calorific value of 30 kJ/g which is equivalent to that for one kg of U235; (b) the mass of U235 i sotope split during the explosion of the atomic bomb with 30 kt trotyl equivalent if the calorific value of trotyl is 4.1 kJ/g.
Ans. (a) the energy liberated in the fission of 1 kg of U235 is
 6.023 x 1023 x 200MeV = 8.21 x 1010kJ
6.023 x 1023 x 200MeV = 8.21 x 1010kJ
The mass of coal with equivalent calorific value is
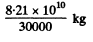 = 2.74 x 106 kg
= 2.74 x 106 kg
(b) The required mass' is
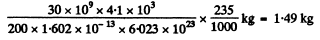
6.262. What amount of heat is liberated during the formation of one gram of He4 from deuterium H2? What mass of coal with calorific value of 30 kJ/g is thermally equivalent to the magnitude obtained?
Ans. The reaction is (in effect).
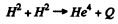
Then
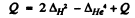
= 0.02820-0.00260
= 0.02560 amu = 23.8 MeV
Hence the energy released in 1 gm of He4 is
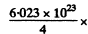 23.8 x 16.02 x 10-13 Joule = 5.75 x 108 kJ
23.8 x 16.02 x 10-13 Joule = 5.75 x 108 kJ
This eneigy can be derived from
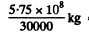 =1.9 x 104 kg of Coal.
=1.9 x 104 kg of Coal.
6.263. Taking the values of atomic masses from the tables, calculate the energy per nucleon which is liberated in the nuclear reaction Li6 + H2 → 2He4. Compare the obtained magnitude with the energy per nucleon liberated in the fission of U235 nucleus.
Ans. The energy released in the reaction
is 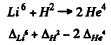
= 0.01513 + 0.01410 - 2 x 0.00 260 amu
= 0.02403 amu = 22.37 MeV
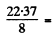 2.796 MeV/nucleon.
2.796 MeV/nucleon.
This should be compared with the value 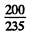 = 0.85 MeV/nucleon
= 0.85 MeV/nucleon
6.264. Find the energy of the reaction Li7 + p → 2He4 if the binding energies per nucleon in Li7 and He4 nuclei are known to be equal to 5.60 and 7.06 MeV respectively.
Ans. The eneigy of reaction
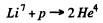
is, 2 x B.E. of He4 - B.E. of Li7
= 8εα - 7εLi = 8 x 7.06 - 7 x 5.60 = 17.3 MeV
6.265. Find the energy of the reaction N14 (α, p) O17 if the kinetic energy of the incoming alpha-particle is Tα = 4.0 MeV and the proton outgoing at an angle θ = 60° to the motion direction of the alpha-particle has a kinetic energy Tp = 2.09 MeV.
Ans. The reaction is N14(a, p)O17
It is given that (in the Lab frame where N14 is at rest) Tα = 4.0MeV. The momentum of incident α particle is
The momentum of outgoing proton is
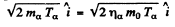
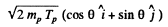
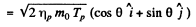
Where 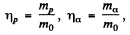
and mo is the mass of O17
The momentum of O17 is
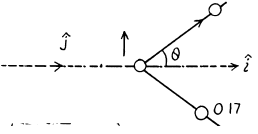
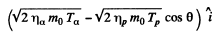
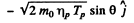
By energy conservation (conservation of energy including rest mass energy and kinetic energy)


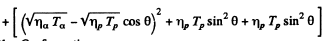
Hence by definition of the Q of reaction
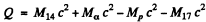

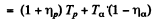
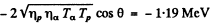
6.266. Making use of the tables of atomic masses, determine the energies of the following reactions: (a) Li7 (p, n) Be7; (b) Be9 (n,γ) Be10; (c) Li7 (α, n) B10); (d) O16 (d, α) N14.
Ans. (a) The reaction is 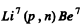 and the energy of reaction is
and the energy of reaction is
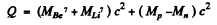
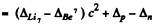
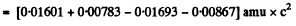
=-1.64 MeV
(b) The reaction is 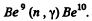
Mass of γ is taken zero. Then
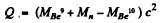
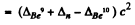
= (0.01219 + 0.00867 - 0.01354) 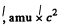
= 6.81 MeV
(c ) The reaction is Li2 (α,n) B10. The energy is
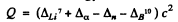
= (0.01601 + 0.00260 - 0.00867 - .01294) amu x c2
= - 2.79 MeV
(d) The reaction is O16 (d , α) N14 The energy of reaction is
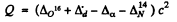
= (- 0.00509 + 0.01410 - 0.00260 - 0.00307) amu x c2
= 3.11 MeV
6.267. Making use of the tables of atomic masses, find the velocity with which the products of the reaction B10 (n, α) Li7 come apart; the reaction proceeds via interaction of very slow neutrons with stationary boron nuclei.
Ans. The reaction is B10 (n, ct) Li1. The energy of the reaction is
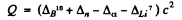
= (0.01294 + 0-00867 - 0.00260 - 0.01601) amu x c2
= 2-79 MeV
Since the incident neutron is very slow and B10 is stationary, the final total momentum must also be zero. So the reaction products must emerge in opposite directions. If their speeds are, repectively, va and vLi
then 4va = 7vLi
and 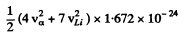 = 2.79 x 1.602 x 10-6
= 2.79 x 1.602 x 10-6
So 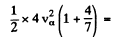 2.70 x 1018 cm2/s2
2.70 x 1018 cm2/s2
or va = 9.27x106 m/s
Then vLi = 5.3 x 106 m/s
6.268. Protons striking a stationary lithium target activate a reaction Li7 (p, n) Be7. At what value of the proton's kinetic energy can the resulting neutron be stationary?
Ans. Q of this reaction (Li7(p, n)Be7) was calculated in problem 266 (a). If is - 1.64 MeV.
We have by conservation of momentum and energy Pp = PBe (since initial Li and final neutron are both at rest)
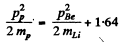
Then 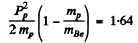
Hence 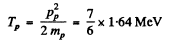 = 1.91MeV
= 1.91MeV
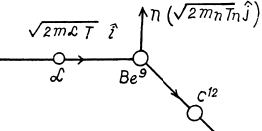
6.269. An alpha particle with kinetic energy T = 5.3 MeV initiates a nuclear reaction Be9 (α, n) C12 with energy yield Q =+5.7 MeV. Find the kinetic energy of the neutron outgoing at right angles to the motion direction of the alpha-particle.
Ans. It is understood that Be9 is initially at rest. The moment of the outgoing neutron is
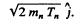 The momentum of C12 is
The momentum of C12 is
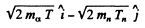
Then by energy conservation

6.270. Protons with kinetic energy T =1.0 MeV striking a lithium target induce a nuclear reaction p + Li7 → 2He4. Find the kinetic energy of each alpha-particle and the angle of their divergence provided their motion directions are symmetrical with respect to that of incoming protons.
Ans. The Q value of the reaction Li7 (p, α) He4 is
= (0.01601 + 0.00783 - 0.00520) amu x c2
= 0.01864 amu x c2 - 17.35 MeV
Since the direction of He4 nuclei is symmetrical, their momenta must also be equal. Let T be the K.E. of each He4. Then

(pp is the momentum of proton). Also

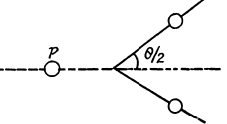
Hence 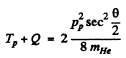
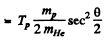
Hence 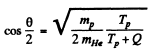
Substitution gives θ = 170.53°
Also 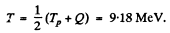
FAQs on Irodov Solutions: Nuclear Reactions- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is a nuclear reaction? |  |
| 2. How are nuclear reactions different from chemical reactions? |  |
| 3. What are the types of nuclear reactions? |  |
| 4. How are nuclear reactions used in power generation? |  |
| 5. What are the risks associated with nuclear reactions? |  |
















