Irodov Solutions: Optics of Moving Sources- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.224. In the Fizeau experiment on measurement of the velocity of light the distance between the gear wheel and the mirror is l = 7.0 km, the number of teeth is z = 720. Two successive disappearances of light are observed at the following rotation velocities of the wheel: n1 = 283 rps and n2 = 313 rps. Find the velocity of light.
Ans. In the Fizean experiment, light disappears when the wheel rotates to bring a tooth in the position formerly occupied by a gap in the time taken by light to go from the wheel to the mirror and back. Thusdistance travelled = 2l Suppose the mth tooth after the gap has come in place of the latter. Then time taken
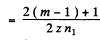 sec. in the first case
sec. in the first case
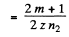 sec in the second case
sec in the second case 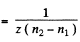
Then 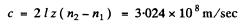
Q.225. A source of light moves with velocity v relative to a receiver. Demonstrate that for v ≪ c the fractional variation of frequency of light is defined by Eq. (5.6a).
Ans. W hen v « c time dilation effect of relativity can be neglected (i.e. t’ ≈ t ) and we can use time in the reference frame fixed to the observer. Suppose the source emits short pulses with intervals T0 . Then in the reference frame fixed to the receiver the distance between two seccessive pulses is 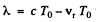 when measured along the observation line.
when measured along the observation line.
Here 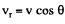 is the projection of the source velocity on the observation line. The frequency of the pulses received by the observer is
is the projection of the source velocity on the observation line. The frequency of the pulses received by the observer is
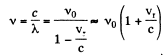
(The formula is accurate to first order only)
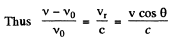
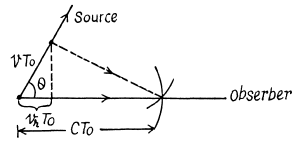
The frequency increases when the source is moving towards the observer.
Q.226. One of the spectral lines emitted by excited He+ ions has a wavelength λ = 410 nm. Find the Doppler shift Δλ of that line when observed at an angle θ = 30° to the beam of moving ions possessing kinetic energy T = 10 MeV
Ans.
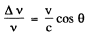 from the previous problem
from the previous problem
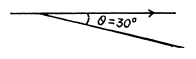
But v λ = c gives an differentiation
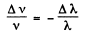
So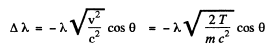
on using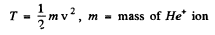
We use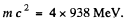 Putting other values
Putting other values
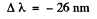
Q.227. When a spectral line of wavelength λ = 0.59 [tm is observed in the directions to the opposite edges of the solar disc along its equator, there is a difference in wavelengths equal to δλ = 8.0 pm. Find the period of the Sun's revolution about its own axis.
Ans. One end of the solar disc is moving towards us while the other end is moving away from us. The angle θ between the direction in which the edges of the disc are moving and the line of observation is small 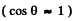 . Thus
. Thus
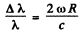
where 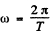 is the angular velocity of the Sun. Thus
is the angular velocity of the Sun. Thus
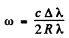
So 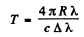
Putting the values 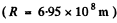
we get T = 24.85days
Q.228. The Doppler effect has made it possible to discover the double stars which are so distant that their resolution by means of a telescope is impossible. The spectral lines of such stars periodically become doublets indicating that the radiation does come from two stars revolving about their centre of mass. Assuming the masses of the two stars to be equal, find the distance between them and their masses if the maximum splitting of the spectral lines is equal to (Δλ/λ)m = 1.2.10-4 and occurs every ζ = 30 days.
Ans. Maximum splitting of die spectral lines will occur when both of the stars are moving in the direction of line of observation as shown. We then have the equations
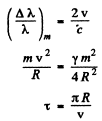
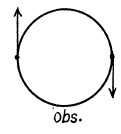
From these we get
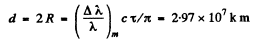
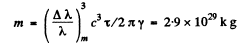
Q.229. A plane electromagnetic wave of frequency coo falls normally on the surface of a mirror approaching with a relativistic velocity V. Making use of the Doppler formula, find the frequency of the reflected wave. Simplify the obtained expression for the case V << c.
Ans. We define the frame S (the lab frame) by the condition of the problem. In this frame the mirror is moving with v elocity v (along say x - ax is) towards left and light of frequency ω0 is approaching it from the left. We introduce the frame S ' whose axes are parallel to those of S but which is moving with velocity v along x axis towards left (so that the mirror is at re st in S'). In S' the frequency of the incident ligh t is
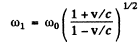
In S.' the reflected light still has frequency ω0 but it is now moving towards left. When we transform back to S this reflected light has the frequency
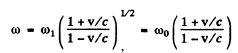
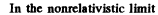
Hence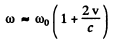
Q.230. A radar operates at a wavelength λ = 50.0 cm. Find the velocity of an approaching aircraft if the beat frequency between the transmitted signal and the signal reflected from the aircraft is equal to Δv = 1.00 kHz at the radar location.
Ans. From the previous problem, the beat frequency is clearly
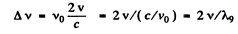
Hence 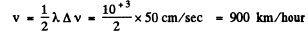
Q.231. Taking into account that the wave phase ωt — kx is an invariant, i.e. it retains its value on transition from one inertial frame to another, determine how the frequency ω and the wave number k entering the expression for the wave phase are transformed. Examine the unidimensional case.
Ans. From the invariance of phase under Lorentz transformations we get
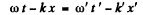
Here 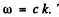 The primed coordinates refer to the frame 5 ' which is moving to the right with velocity v
The primed coordinates refer to the frame 5 ' which is moving to the right with velocity v
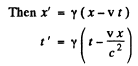
Where 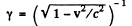
Substituting and equating the coffiecients of t
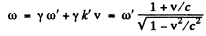
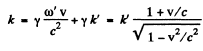
Q.232. How fast does a certain nebula recede if the hydrogen line λ = 434 nm in its spectrum is displaced by 130 nm toward longer wavelengths?
Ans. Frome the previous problem using
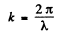
We get 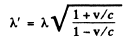
Thus 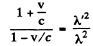
or 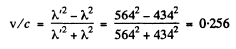
Q.233. How fast should a car move for the driver to perceive a red traffic light  as a green one
as a green one 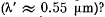
Ans. As in the previous problem
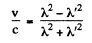
so 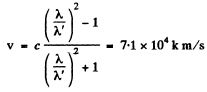
Q.234. An observer moves with velocity 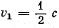 along a straight line. In front of him a source of monochromatic light moves with velocity
along a straight line. In front of him a source of monochromatic light moves with velocity 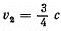 in the same direction and along the same straight line. The proper frequency of light is equal to ωo. Find the frequency of light registered by the observer.
in the same direction and along the same straight line. The proper frequency of light is equal to ωo. Find the frequency of light registered by the observer.
Ans. We go to the frame in which the observer is at rest. In this frame the velocity of the source of light is, by relativistic velocity addition foumula,
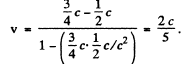
When this source emits light of proper frequency ωo the frequency recorded by observer will be
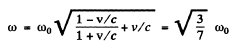
Note that ω < ωo as the source is moving away from the observer (red shift).
FAQs on Irodov Solutions: Optics of Moving Sources- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the Doppler effect in optics? |  |
| 2. How does the Doppler effect affect the perceived color of a moving source of light? |  |
| 3. Can the Doppler effect be observed in everyday situations? |  |
| 4. How is the Doppler effect related to the speed of the moving source? |  |
| 5. Are there any applications of the Doppler effect in optics? |  |

|
Explore Courses for JEE exam
|

|

















