Irodov Solutions: Optics of Moving Sources- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.235. One of the spectral lines of atomic hydrogen has the wavelength λ =656.3 nm. Find the Doppler shift Δλ of that line when observed at right angles to the beam of hydrogen atoms with kinetic energy T = 1.0 MeV (the transverse Doppler effect).
Ans. In transverse Doppler effect.

So 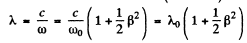
Hence 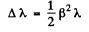
Using 
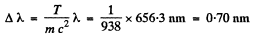
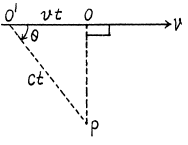
Q.236. A source emitting electromagnetic signals with proper frequency (ωo = 3.0.1010 s-1 moves at a constant velocity v = 0.80 c along a straight line separated from a stationary observer P by a distance l (Fig. 5.37). Find the frequency of the signals perceived by the observer at the moment when
(a) the source is at the point O;
(b) the observer sees it at the point O.
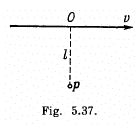
Ans. (a) If light is received by the observer at P at the moment when the source is at <9, it must have been emitted by the source when it was at O' and travelled along
In the frame of the observer, the frequency of the light is ω while its wave vector is
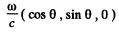
we can calculate the value of ω by relating it to proper frequency ω. The relation is
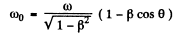
(To derive the formula is this form it is easiest to note that 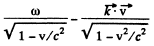 is an invariant which takes the value co0 in the rest frame of the source).
is an invariant which takes the value co0 in the rest frame of the source).
Thus 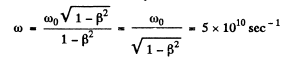
(b) For the light to be received at the instant observer sees the source at O, light must be emitted when the observer is at O at 90° = θ

Then as before  or
or 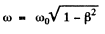
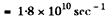
In this case the observer will receive light along OP and he will “see” that the source is at O even though the source will have moved ahead at the instant the light is received.
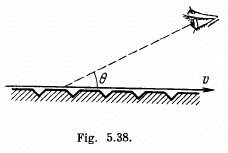
Q.237. A narrow beam of electrons passes immediately over the surface of a metallic mirror with a diffraction grating with period d = 2.0 tim inscribed on it. The electrons move with velocity v, comparable to c, at right angles to the lines of the grating. The trajectory of the electrons can be seen in the form of a strip, whose colouring depends on the observation angle θ (Fig. 5.38). Interpret this phenomenon. Find the wavelength of the radiation observed at an angle θ = 45°.
Ans. An electron moving in front of a metal mirror sees an image chaige of equal and opposite type. The two together constitute a dipole. Let us look at the problem in the rest frame of the electron. In this frame the grating period is Lorenz contracted to

Because the metal has etchings the dipole moment of electron-image pair is periodically distuibed with a period 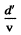
The corresponding frequency is 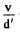 which is also the proper frequency of radiation emitted. Due to Doppler effect the frequency observed at an angle 0 is
which is also the proper frequency of radiation emitted. Due to Doppler effect the frequency observed at an angle 0 is
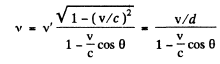
The corresponding wave length is 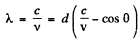
Putting
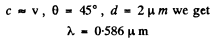
Q.238. A gas consists of atoms of mass m being in thermodynamic equilibrium at temperature T. Suppose ωo is the natural frequency of light emitted by the atoms. (a) Demonstrate that the spectral distribution of the emitted light is defined by the formula
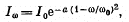
(I0 is the spectral intensity corresponding to the frequency ωo, 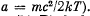
(b) Find the relative width Δω/ω0 of a given spectral line, i.e. the width of the line between the frequencies at which 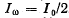 .
.
Ans. (a) Let vx be the projection of the velocity vector of the radiating atom on the observation direction. The number of atoms with projections falling within the interval vx and
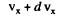
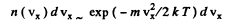
The frequency of light emitted by the atoms moving with velocity vx is 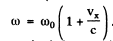 . From the expressions the frequency distribution of atoms can be found
. From the expressions the frequency distribution of atoms can be found
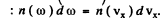 Now using
Now using
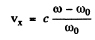
we get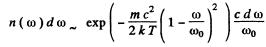
Now the spectral radiation density 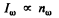
Hence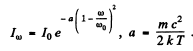
(The constant of proportionality is fixed by I0.)
(b) On putting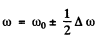 and demanding
and demanding
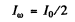
we get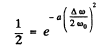
so 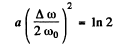
Hence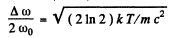
and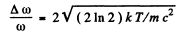
Q.239. A plane electromagnetic wave propagates in a medium moving with constant velocity V ≪ c relative to an inertial frame K. Find the velocity of that wave in the frame K if the refractive index of the medium is equal to n and the propagation direction of the wave coincides with that of the medium.
Ans. In vacuum inertial frames are all equivalent; the velocity of light is c in any frame. This equivalence of inertial frames does not hold in material media and here the frame in which the m edium is at rest is singled out It is in this fram e that the velocity of light is 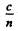 where n is the refractive in desc of light for that medium.
where n is the refractive in desc of light for that medium.
The velocity of light in the frame in which the medium is moving is then by the law of addition of velocities
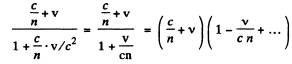
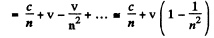
This is the velocity of light in the medium in a frame in which the medium is moving with velocity v « c .
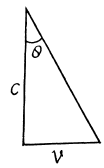
Q.240. Aberration of light is the apparent displacement of stars attributable to the effect of the orbital motion of the Earth. The direction to a star in the ecliptic plane varies periodically, and the star performs apparent oscillations within an angle δθ = 41". Find the orbital velocity of the Earth.
Ans. Although speed of light is the same in all inertial frames of reference according to the principles of relativity, the direction of a light ray can appear different in different frames. This phenomenon is called aberration and to first order in 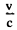 , can be calculated by the elementary law of addition of velocities applied to light waves.
, can be calculated by the elementary law of addition of velocities applied to light waves.
The angle of aberration is
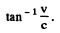
and in the present case it equals 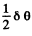 on either side. Thus equating
on either side. Thus equating
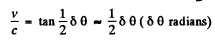
or 
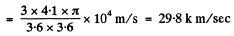
Q.241. Demonstrate that the angle θ between the propagation direction of light and the x axis transforms on transition from the reference frame K to K' according to the formula
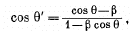
where β = V/c and V is the velocity of the frame K' with respect to the frame K. The x and x' axes of the reference frames coincide.
Ans. We consider the invariance of the phase of a wave moving in the x - y plane. We write
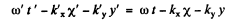
From Lorcntz transformations, L.H.S.
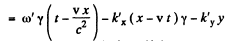
so equating
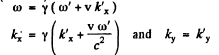
so inverting

writing 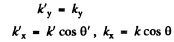
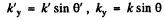
we get on using
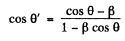

We see that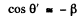
if 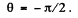
Then 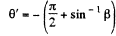
This is exactly what we get from elementary nonrelativistic law of addition of velocities,
Q.242. Find the aperture angle of a cone in which all the stars located in the semi-sphere for an observer on the Earth will be visible if one moves relative to the Earth with relativistic velocity V differing by 1.0% from the velocity of light. Make use of the formula of the foregoing problem.
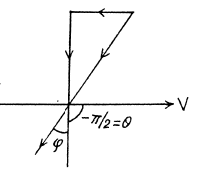
Ans. The statement of the problem is not quite properly worked and is in fact misleading. The correct situation is described below. We consider,for simplicity, stars in the x - z plane. Then the previous formula is applicable, and we have
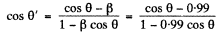
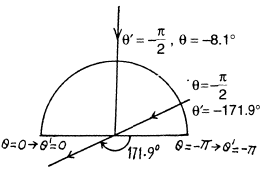
The distribution of θ' is given in the diagram below The light that appears to come from the forward quadrant in the frame  is compressed into an angle of magnitude + 8.1° in the forward direction while the remaining stars are spread out.
is compressed into an angle of magnitude + 8.1° in the forward direction while the remaining stars are spread out.
The three dimensional distribution can also be found out from the three dimensional generalization of the formula in the previous problems.
Q.243. Find the conditions under which a charged particle moving uniformly through a medium with refractive index n emits light (the Vavilov-Cherenkov effect). Find also the direction of that radiation. Instruction. Consider the interference of oscillations induced by the particle at various moments of time.
Ans. The field induced by a charged particle moving with velocity V excites the atoms of the medium turning them into sources of light waves. Let us consider two arbitrary points A and B along the path of the particle. The light waves emitted from these points when the particle passes them reach the point P simultaneously and reinforce each other provided they are in phase which is the case is general if the time taken by the light wave to propagate from the point A to the point C is equal to that taken by the particle to fly over the distance AB. Hence we obtain
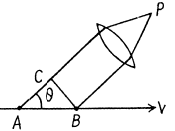

where  is the phase velocity of light. It is evident that the radiation is possible only if V >v i.e. when the velocity of the particle exceeds the phase velocity of light in the medium.
is the phase velocity of light. It is evident that the radiation is possible only if V >v i.e. when the velocity of the particle exceeds the phase velocity of light in the medium.
Q.244. Find the lowest values of the kinetic energy of an electron and a proton causing the emergence of Cherenkov's radiation in a medium with refractive index n = 1.60. For what particles is this minimum value of kinetic energy equal to Tmin = 29.6 MeV?
Ans. We must have
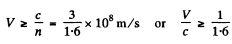
For electrons this means a K.E. greater than

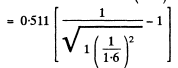
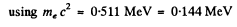
For protons with 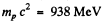
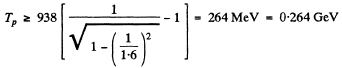
Also 
Then 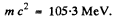 This is very nearly the mass of means.
This is very nearly the mass of means.
Q.245. Find the kinetic energy of electrons emitting light in a medium with refractive index n = 1.50 at an angle θ = 30° to their propagation direction.
Ans. From 
we get 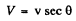
so 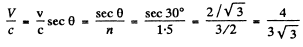
Thus for electoms
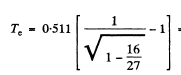
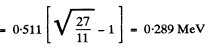
Generally 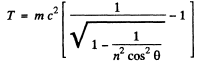

|
Explore Courses for JEE exam
|

|

















