Irodov Solutions: Polarization of Light- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.157. A plane monochromatic wave of natural light with intensity Io falls normally on a screen composed of two touching Polaroid half-planes. The principal direction of one Polaroid is parallel, and of the other perpendicular, to the boundary between them. What kind of diffraction pattern is formed behind the screen? What is the intensity of light behind the screen at the points of the plane perpendicular to the screen and passing through the boundary between the Polaroids?
Ans. Natural light can be considered to be an incoherent mixture of tw o plane polarized light of intensity l0/ 2 with mutually perpendicular planes of vibration. The screen cbnpsting of the two Polaroid half-planes acts as an opaque half-screen fo r one or th^ other of these light waves. The resulting diffraction pattern has the alterations in intensity (in the illuminated region ) characteristic of a straight edge on both sides of the boundary.
A t the boundary the intensity due to either component is
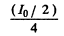
and the total intensity is  (Recall that when light o f intensity I0 is incident on a straight edge, the illuminance in front o f the edge is l0/4 ) .
(Recall that when light o f intensity I0 is incident on a straight edge, the illuminance in front o f the edge is l0/4 ) .
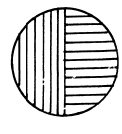
Q.158. A plane monochromatic wave of natural light with intensity Iofalls normally on an opaque screen with round hole corresponding to the first Fresnel zone for the observation point P. Find the intensity of light at the point P after the hole was covered with two identical Polaroids whose principal directions are mutually perpendicular and the boundary between them passes
(a) along the diameter of the hole;
(b) along the circumference of the circle limiting the first half of the Fresnel zone.
Ans. (a) Assume first that there is no polaroid and the amplitude due to the entire hole which extends over the first Fresnel zone is A1
Then, we know, as usual, 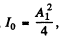
When the polaroid is introduced as shown above, each half transmits only the corresponding polarized light. If the full hole were covered by one polaroid the amplitude transmitted w ill be 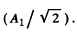
Therefore the amplitude transmitted in the present case will be 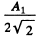 through either half.
through either half.
Since these transmitted waves are polarized in mutually perpendicular planes, the total intensity will be
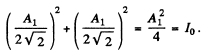
(b) We interpret the problem to mean that the two polaroid pieces are separated along the circumference o f the circle limiting the first half o f the Fresnel zone. (This however is inconsistent with the polaroids being identical in shape; however no other interpretation makes sense.) From (5 .103) and the previous problems we see that the amplitudes o f the waves transmitted through the two parts is
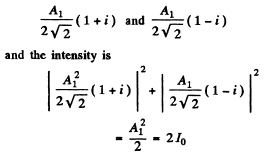
Q.159. A beam of plane-polarized light falls on a polarizer which rotates about the axis of the ray with angular velocity ω = 21 rad/s. Find the energy of light passing through the polarizer per one revolution if the flux of energy of the, incident ray is equal to φ0 = = 4.0 mW.
Ans. When the polarizer rotates with angular velocity ω its instantaneous principal direction makes angle ωt from a reference direction which we choose to be along the direction of vibration of the plane polarized incident light The transmitted flux at this instant is

and the total energy passing through the polarizer per revolution is

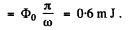
Q.160. A beam of natural light falls on a system of N = 6 Nicol prisms whose transmission planes are turned each through an angle φ = 30° with respect to that of the foregoing prism. What fraction of luminous flux passes through this system?
Ans. Let I0 intensity of the incident beam.
Then the intensity of the beam transmitted through the first Nicol prism is
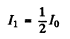
and through the 2nd prism is
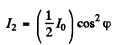
Through the Nth prism it will be
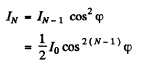
Hence fraction transmitted
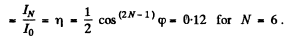
and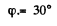
Q.161. Natural light falls on a system of three identical in-line Polaroids, the principal direction of the middle Polaroid forming an angle φ = 60° with those of two other Polaroids. The maximum transmission coefficient of each Polaroid is equal to τ = 0.81 when plane-polarized light falls on them. How many times will the intensity of the light decrease after its passing through the system?
Ans. When natural light is incident on the first polaroid, the fraction transmitted will be 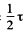 (only the component polarized parallel to the principal direction of the polaroid will go).
(only the component polarized parallel to the principal direction of the polaroid will go).
The emergent light will be plane polarized and on passing through the second polaroid will be polarized in a different direction (corresponding to the principal direction of the 2nd polaroid) and the intensity will have decreased further by 
In the third polaroid the direction of polarization will again have to change by cp thus only a fraction  will go through.
will go through.
Finally
Thus the intensity will have decreased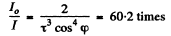
for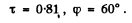
Q.162. The degree of polarization of partially polarized light is P = 0.25. Find the ratio of intensities of the polarized component of this light and the natural component.
Ans. Suppose the partially polarized light consists of natural light of intensity l1 and plane polarized light of intensity I2 with direction of vibration parallel to, say, x - axis.
Then when a polaroid is used to transmit it, the light transmitted will have a maximum intensity
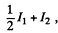
when the principal direction of the polaroid is parallel to x - axis, and will have a minimum

Thus 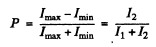
so 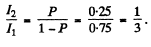
Q.163. A Nicol prism is placed in the way of partially polarized beam of light. When the prism is turned from the position of maximum transmission through an angle ω = 60°, the intensity of transmitted light decreased by a factor of η = 3.0. Find the degree of polarization of incident light.
Ans. If, as above,
I1 = intensity of natural component
I2 = intensity o f plane polarized component
Then 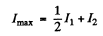
and 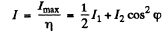
so 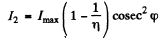
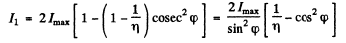
Then 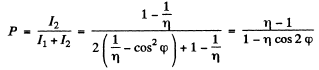
On putting 
we get 
Q.164. Two identical imperfect polarizers are placed in the way of a natural beam of light. When the polarizers' planes are parallel, the system transmits η = 10.0 times more light than in the case of crossed planes. Find the degree of polarization of light produced
(a) by each polarizer separately;
(b) by the whole system when the planes of the polarizers are parallel.
Ans. Let us represent the natural ligh t as a sum o f two mutually perpendicular components, both with intensity I0 . Suppose that each polarizer transmits a fraction α1 o f the light with oscillation plane parallel to the prinicipal direction o f the polarizer and a fraction α2 with oscillation plane perpendicular to the principal direction o f the polaizer. Then the intensity o f light transmitted through the two polarizers is equal to
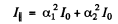
when their principal direction are parallel and
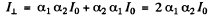
when they are crossed. But
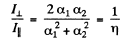
so 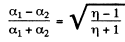
(a) Now the degree of polarization produced by either polarizer when used singly is

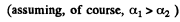
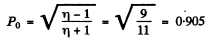
(b) When both polarizer are used with their principal directions parallel, the transmitted light, when analysed, has
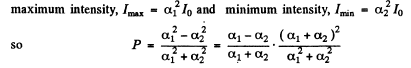
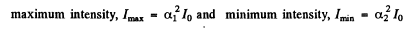
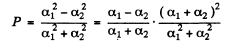
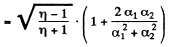
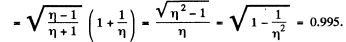
Q.165. Two parallel plane-polarized beams of light of equal intensity whose oscillation planes N1 and N2 form a small angle ω between them (Fig. 5.30) fall on a Nicol prism. To equalize the intensities of the beams emerging behind the prism, its principal direction N must be aligned along the bisecting line A or B. Find the value of the angle φ at which the rotation of the Nicol prism through a small angle δφ ≪ φ from the position A results in the fractional change of intensities of the beams AIII by the value η = 100 times exceeding that resulting due to rotation through the same angle from the position B.
Ans. If the principal direction N o f the N icol is along A or B , the intensity of light transmitted is the same whether the light incident is one with oscillation plane N1 or one with N2. If N makes an angle δφ with A as shown then the fractional difference in intensity transmitted (when the lig h t incident is N1 or N2 ) is
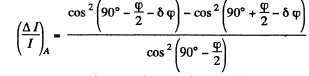
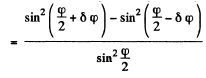
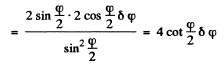
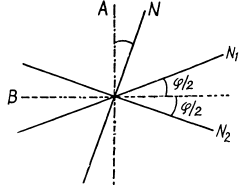
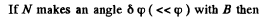
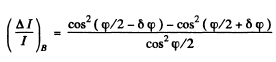
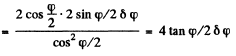
Thus 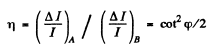
or 
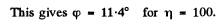
Q.166. Resorting to the Fresnel equations, demonstrate that light reflected from the surface of dielectric will be totally polarized if the angle of incidence θ1, satisfies the condition tanθ1 = n, where n is the refractive index of the dielectric. What is in this case the angle between the reflected and refracted rays?
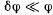
Ans. Fresnel equations read
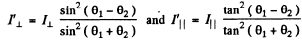
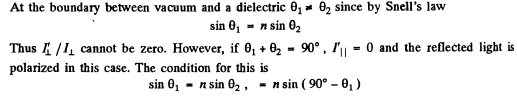
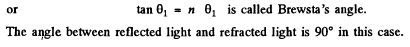
Q.167. Natural light falls at the Brewster angle on the surface of glass. Using the Fresnel equations, find (a) the reflection coefficient; (b) the degree of polarization of refracted light.
Ans. (a) From Fresnel’s equations
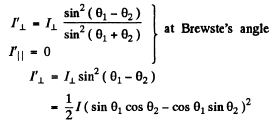
Now
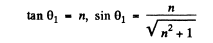
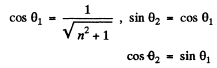
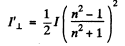
Thus reflection coefficient
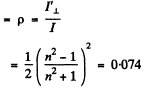
on putting n = 1.5
(b) For the refracted light
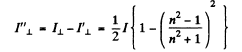
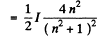
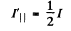
at the Brewster’s angle.
Thus the degree of polarization of the refracted light is
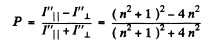
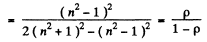
On putting p = 0.074 we get P = 0.080 .
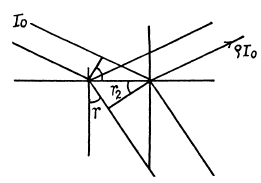
Q.168. A plane beam of natural light with intensity l0 falls on the surface of water at the Brewster angle. A fraction p = 0.039 of luminous flux is reflected. Find the intensity of the refracted beam.
Ans. he energy transmitted is, by conservation of energy, the difference between incident energy and the reflected energy. However the intensity is affected by the change of the cross section of the beam by refraction. Let Ai, Ar, At be the cross sections of the incident, reflected and transmitted beams. Then
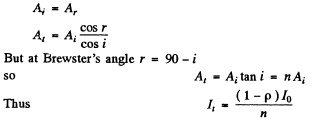
Q.169. A beam of plane-polarized light falls on the surface of water at the Brewster angle. The polarization plane of the electric vector of the electromagnetic wave makes an angle λ = 45° with the incidence plane. Find the reflection coefficient.
Ans. The amplitude of the incident component whose oscillation vector is perpendicular to the plane of incidence is
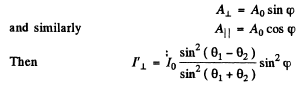
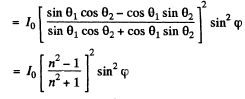
Hence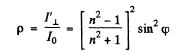
Putting n = 1.33 for water we get p = 0.0386
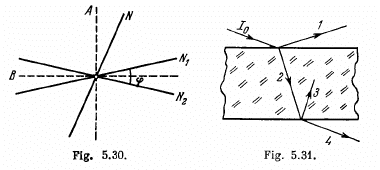
Q.170. A narrow beam of natural light falls on the surface of a thick transparent plane-parallel plate at the Brewster angle. As a result, a fraction p = 0.080 of luminous flux is reflected from its top surface. Find the degree of polarization of beams 1-4 (Fig. 5.31)
Ans. Since natural light is incident at the Brewster’s angle, the reflected light 1 is completely polarized and P1 = 1.
Similarly the ray 2 is incident on glass air surface at
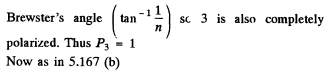
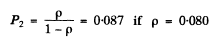
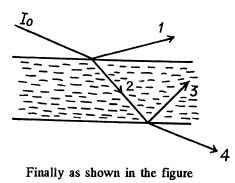
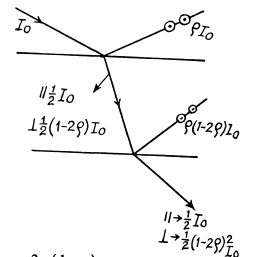
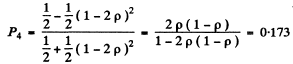
Q.171. A narrow beam of light of intensity l0 falls on a planeparallel glass plate (Fig. 5.31) at the Brewster angle. Using the Fresnel equations, find:
(a) the intensity of the transmitted beam 1:4 if the oscillation plane of the incident plane-polarized light is perpendicular to the incidence plane;
(b) the degree of polarization of the transmitted light if the light falling on the plate is natural.
Ans. (a) In this case from Fresnel's equations
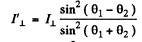
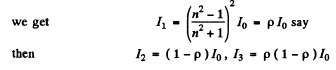
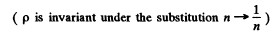
finally 
(b) Suppose p' = coeflGcient of reflection for the component of light whose electric vector oscillates at right angles to the incidence plane.
From Fresnel's equations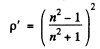
Then in the transmitted beam we have a partially polarized beam which is a superposition of two components with intensities
components with intensities
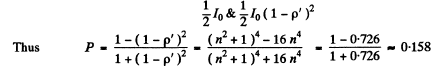
Q.172. A narrow beam of natural light falls on a set of N thick plane-parallel glass plates at the Brewster angle. Find: (a) the degree P of polarization of the transmitted beam; (b) what P is equal to when N = 1, 2, 5, and 10.
Ans. (a) When natural light is incident on a glass plate at Brewster’s angle, the transmitted light has
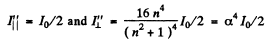
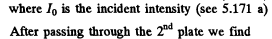
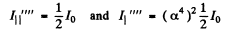
Thus After N Plates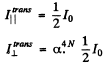
Hence 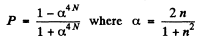
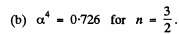
Thus
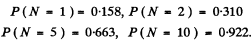
Q.173. Using the Fresnel equations, find:
(a) the reflection coefficient of natural light falling normally on the surface of glass;
(b) the relative loss of luminous flux due to reflections of a paraxial ray of natural light passing through an aligned optical system comprising five glass lenses (secondary reflections of light are to be neglected).
Ans.

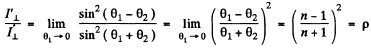
Similarity 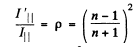
Thus 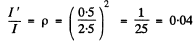
(b) The reflected light at the first surface has the intensity
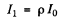
Then the transmitted light has the intensity
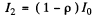
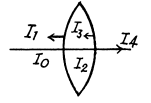
At the second surface where light emerges from glass into air, the reflection coefficient is again p because
FAQs on Irodov Solutions: Polarization of Light- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is polarization of light? |  |
| 2. How does polarization of light occur? |  |
| 3. What are the types of polarized light? |  |
| 4. How can polarized light be detected? |  |
| 5. What are the applications of polarized light? |  |

|
Explore Courses for JEE exam
|

|

















