Irodov Solutions: Polarization of Light- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.174. A light wave falls normally on the surface of glass coated with a layer of transparent substance. Neglecting secondary reflections, demonstrate that the amplitudes of light waves reflected from the two surfaces of such a laver will be equal under the condi- tion  where n' and n are the refractive indices of the layer and the glass respectively.
where n' and n are the refractive indices of the layer and the glass respectively.
Ans. Suppose the incident light can be decomposed into waves with intensity  with oscillations of the electric vectors parallel and perpendicular to the plane of incidence.
with oscillations of the electric vectors parallel and perpendicular to the plane of incidence.
For normal incidence we have from Fresnel equations
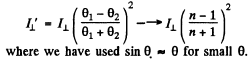
Similarly 

Then the refracted wave will be

At the interface with glass

we see that

This shows that the light reflected as a fraction of the incident light is the same on the two surfaces if 
Note:- The statement of the problem given in the book is incorrect. Actual amplitudes are not equal; only the reflectance is equal.
Q.175. A beam of natural light falls on the surface of glass at an angle of 45°. Using the Fresnel equations, find the degree of polarization of
(a) reflected light;
(b) refracted light.
Ans. Here

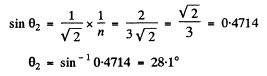
Hence

Thus 
(1) Degree of polarization P of the reflected light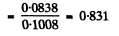
(b) By conservation of energy
Thus
Q.176. Using Huygens's principle, construct the wavefronts and the propagation directions of the ordinary and extraordinary rays in a positive uniaxial crystal whose optical axis
(a) is perpendicular to the incidence plane and parallel to the surface of the crystal;
(b) lies in the incidence plane and is parallel to the surface of the crystal;

(c) lies in the incidence plane at an angle of 45° to the surface of the crystal, and light falls at right angles to the optical axis.
Ans. The wave surface of a uniaxial crystal consists of two sheets of which one is a sphere while the other is an ellipsoid of revolution.
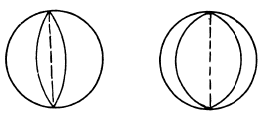
The optic axis is the line joining the points of contact.
To makes the appropriate Huyghen’s construction we must draw the relevant section of the wave surface inside the crystal and determine the directions of the ordinary and extraordinary rays. The result is as shown in Fig. 42 (a, b & c) of the answers
Q.177. A narrow beam of natural light with wavelength λ = 589 nm falls normally on the surface of a Wollaston polarizing prism made of Iceland spar as shown in Fig. 5.32. The optical axes of the two parts of the prism are mutually perpendicular. Find the angle 8 between the directions of the beams behind the prism if the angle 0 is equal to 30°.
Ans. In a uniaxial crystal, an unpolarized beam of light (or even a polarized one) splits up into O (for ordinary) and E (for extraordinary) light waves. The direction of vibration in the O and E waves are most easily specified in terms of the O and E principal planes. The principal plane of the ordinary wave is defined as the plane containing the O ray and the optic axis. Similarly the principal plane of the E wave is the plane containing the E ray and the optic axis.
In terms of these planes the following is true : The O vibrations are perpendicular to the principal plane of the O ray while the E vibrations are in the principal plane of the E ray.

When we apply this definition to the wollaston prism we find the following :
When unpolarized light enters from the left the O and E waves travel in the same direction but with different speeds. The O ray on the left has its vibrations normal to the plane of the paper and it becomes E ray on crossing the diagonal boundary of the two prism similarly the E ray on the left becomes O ray on the right In this case Snell’s law is applicable only approximately. The two rays are incident on the boundary at an angle θ and in the right prism the ray which we have called O ray on the right emerges at

Similarly the E ray on the right emerges within the prism at

This means that the O ray is incident at the boundary between the prism and air at
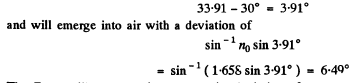
The E ray will emeige with an opposite deviation of
Hence 
This result is accurate to first order in  because S nell’s law holds when
because S nell’s law holds when 
Q.178. What kind of polarization has a plane electromagnetic wave if the projections of the vector E on the x and y axes are perpendicular to the propagation direction and are defined by the following equations:

Ans. The wave is moving in the direction of z - axis

so the of the electric vector m oves along a circle. For the right handed coordinate system this represents circular anticlockwise polarization when observed towards the incoming wave
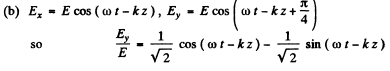

This is clearly an ellipse. By comparing with the previous case (compare the phase of Ey in the two cases) we see this represents elliptical clockwise polarization when viewed towards the incoming wave.
We write the equations as

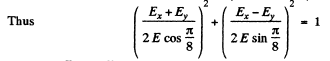
Since  the major axis is in the direction of the straight line y = x.
the major axis is in the direction of the straight line y = x.

Q.179. One has to manufacture a quartz plate cut parallel to its optical axis and not exceeding 0.50 mm in thickness. Find the maximum thickness of the plate allowing plane-polarized light with wavelength λ = 589 nm
(a) to experience only rotation of polarization plane;
(b) to acquire circular polarization after passing through that plate.
Ans.

In a quartz plate cut parallel to its optic axis, plane polarized light incident normally from the left divides itself into O and E waves which move in the same direction with different speeds and as a result acquire a phase difference. This phase difference is

where d = thickness of the plate. In general this makes the emergent light elliptically polarized.
(a) For emergent light to experience only rotation of polarization plane
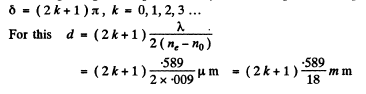
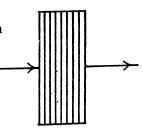
The maximum value of (2k+1) for which this is

(b) For circular polarization 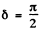
modulo 
so 
Now 
The nearest integer less than this which is of the form  For this d = 0.4749 mm
For this d = 0.4749 mm
Q.180. A quartz plate cut parallel to the optical axis is placed between two crossed Nicol prisms. The angle between the principal directions of the Nicol prisms and the plate is equal to 45°. The thickness of the plate is d = 0.50 mm. At what wavelengths in the interval from 0.50 to 0.60 μm is the intensity of light which passed through that system independent of rotation of the rear prism? The difference of refractive indices for ordinary and extraordinary rays in that wavelength interval is assumed to be Δn = 0.0090.
Ans. As in the previous problem the quartz plate introduces a phase difference δ between the O & E components. When  the resultant wave is circularly polarized.
the resultant wave is circularly polarized.
In this case intensity is independent of the rotation of the rear prism. Now
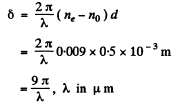
 The relevant values of δ have to be chosen in the form
The relevant values of δ have to be chosen in the form
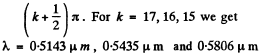
These are the values of δ which lie between 0.50μm and 0.60μm .
Q.181. White natural light falls on a system of two crossed Nicol prisms having between them a quartz plate 1.50 mm thick, cut parallel to the optical axis. The axis of the plate forms an angle of 45° with the principal directions of the Nicol prisms. The light transmitted through that system was split into the spectrum. How many dark fringes will be observed in the wavelength interval from 0.55 to 0.66 μm? The difference of refractive indices for ordinary and extraordinary rays in that wavelength interval is assumed to be equal to 0.0090.
Ans. As in the previous two problems the quartz plate will introduce a phase difference δ. The light on passing through the plate will remain plane polarized only for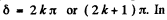 the latter case the plane of polarization of the light incident on the plate will be rotated by 90° by it so light passing through the analyser (which was originally crossed) will be a maximum. Thus dark bands will be observed only for those λ for which
the latter case the plane of polarization of the light incident on the plate will be rotated by 90° by it so light passing through the analyser (which was originally crossed) will be a maximum. Thus dark bands will be observed only for those λ for which


Q.182. A crystalline plate cut parallel to its optical axis is 0.25 mm thick and serves as a quarter-wave plate for a wavelength λ = 530 nm. At what other wavelengths of visible spectrum will it also serve as a quarter-wave plate? The difference of refractive indices for extraordinary and ordinary rays is assumed to be constant and equal to ne — no =0 .0090 at all wavelengths of the visible spectrum.
Ans. Here

We check that for

These are the only values of λ, for which the plate acts as a quarter wave plate.
Q.183. A quartz plate cut parallel to its optical axis is placed between two crossed Nicol prisms so that their principle directions form an angle of 45° with the optical axis of the plate. What is the minimum thickness of that plate transmitting light of wavelength λ1 = 643 nm with maximum intensity while greatly reducing the intensity of transmitting light of wavelength λ2 = 564 nm? The difference of refractive indices for extraordinary and ordinary rays is assumed to be equal to ne — no = 0 .0090 for both wavelengths.
Ans. Between crossed Nicols, a quartz plate, whose optic axis makes 45° with the principal directions of the Nicols, must introduce a phase difference of (2k + 1) ji so as to transmit the incident light (of that wavelength) with maximum intensity. For in this case the plane of polarization of the light emerging from the polarizer will be rotated by 90° and will go through the analyser undiminished. Thus we write for light of wavelengths 643 nm
 (1)
(1)
To nearly block light of wavelength 564 nm we require
 (2)
(2)

This is not quite an integer but is close to one. This means that if we take 2 k = 6 equations (1) can be satisfied exactly while equation (2) will hold approximately. Thus

Q.184. A quartz wedge with refracting angle  is inserted between two crossed Polaroids. The optical axis of the wedge is parallel to its edge and forms an angle of 45° with the principal directions of the Polaroids. On transmission of light with wavelength λ = 550 nm through this system, an interference fringe pattern is formed. The width of each fringe is Δx = 1.0 mm. Find the
is inserted between two crossed Polaroids. The optical axis of the wedge is parallel to its edge and forms an angle of 45° with the principal directions of the Polaroids. On transmission of light with wavelength λ = 550 nm through this system, an interference fringe pattern is formed. The width of each fringe is Δx = 1.0 mm. Find the

difference of refractive indices of quartz for ordinary and extraordinary rays at the wavelength indicated above.
Ans. If a ray traverses the wedge at a distance x below the joint, then the distance that the ray moves in the wedge is
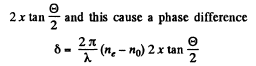
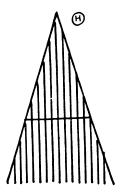
between the E and O wave components of the ray. For a general x the resulting light is elliptically polarized and is not completely quenched by the analyser polaroid. The condition for complete quenching is

That for maximum brightness is

The fringe width is given by

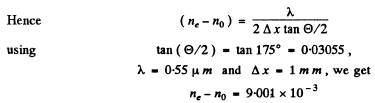
Q.185. Natural monochromatic light of intensity l0 falls on a system of two Polaroids between which a crystalline plate is inserted, cut parallel to its optical axis. The plate introduces a phase difference δ between the ordinary and extraordinary rays. Demonstrate that the intensity of light transmitted through that system is equal to

where φ and φ' are the angles between the optical axis of the crystal and the principal directions of the Polaroids. In particular, consider the cases of crossed and parallel Polaroids.
Ans. Light emerging from the first polaroid is plane polarized with amplitude A where N1 is the principal direction of the polaroid and a vibration of amplitude can be resolved into two vibration : E wave with vibration along the optic axis of amplitude A cosφ and the O wave with vibration perpendicular to the optic axis and having an amplitude A sinφ. These acquire a phase difference δ on passing through the plate. The second polaroid transmits the components


What emerges from the second polaroid is a set of two plane polarized waves in the same direction and same plane of polarization but phase difference δ. They interfere and produce a wave of amplitude squared




Parallel polaroids :

With  the conditions for the maximum and minimum are easily found to be that shown in the answer.
the conditions for the maximum and minimum are easily found to be that shown in the answer.
FAQs on Irodov Solutions: Polarization of Light- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is polarization of light? |  |
| 2. How does polarization of light occur? |  |
| 3. What are the applications of polarization of light? |  |
| 4. Can all types of light be polarized? |  |
| 5. How is polarization of light useful in scientific research? |  |
















