Irodov Solutions: Polarization of Light- 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
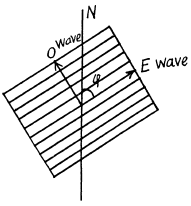
Q.186. Monochromatic light with circular polarization falls normally on a crystalline plate cut parallel to the optical axis. Behind the plate there is a Nicol prism whose principal direction forms an angle φ with the optical axis of the plate. Demonstrate that the intensity of light transmitted through that system is equal to
where δ is the phase difference between the ordinary and extraordinary rays which is introduced by the plate.
Ans. Let the circularly polarized light be resolved into plane polarized components of amplitude A0 with a phase
difference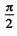 between then
between then
On passing through the crystal the phase difference becomes 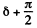 and the components of the E and O wave in the direction N are respectively
and the components of the E and O wave in the direction N are respectively 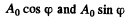
They interfere to produce the amplitude squared
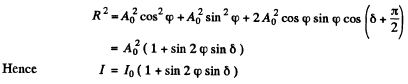
Here I0 is the intensity of die light transmitted by the polaroid when there is no crystal plate
Q.187. Explain how, using a Polaroid and a quarter-wave plate made of positive uniaxial crystal  o distinguish
o distinguish
(a) light with left-hand circular polarization from that with right-hand polarization;
(b) natural light from light with circular polarization and from the composition of natural light and that with circular polarization.
Ans. (a) The light with right circular polarization (viewed against the oncoming light, this means that the light vector is moving clock wise.) becomes plane polarized on passing through a quarter-wave plate. In this case the direction of oscillations of the electric vector of the electromagnetic wave forms an angle of + 45° with the axis of the crystal OO' (see Fig (a) below). In the case of left hand circular polarizations, this angle will be - 45° ( Fig (b)).
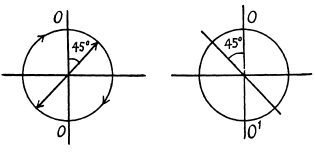
(b) If for any position of the plate the rotation of the polaroid (located behind the plate) does not bring about any variation in the intensity of the transmitted light, the incident ligit is unpolarized (i.e. natural). If the intensity of the transmitted light can drop to zero on rotating the analyzer polaroid for some position of the quarter wave plate, the incident light is circularly polarized. If it varies but does not drop to zero, it must be a mixture of natural and circularly polarized light.
Q.188. Light with wavelength λ falls on a system of crossed polarizer P and analyzer A between which a Babinet compensator C

is inserted (Fig. 5.33). The compensa- tor consists of two quartz wedges with the optical axis of one of them being parallel to the edge, and of the other, perpendicular to it. The principal direc- tions of the polarizer and the analyser form an angle of 45° with the optical axes of the compensator. The refracting angle of the wedges is equal to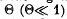
the difference of refractive indices of quartz is 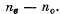 The insertion of investigated birefringent sample S, with the optical axis oriented as shown in the figure, results in displacement of the fringes upward by δx mm. Find:
The insertion of investigated birefringent sample S, with the optical axis oriented as shown in the figure, results in displacement of the fringes upward by δx mm. Find:
(a) the width of the fringe Δx;
(b) the magnitude and the sign of the optical path difference of ordinary and extraordinary rays, which appears due to the sample S.
Ans. The light from P is plane polarized with its electric vector vibrating at 45° with the plane of the paper. At first the sample S is absent Light from P can be resolved into components vibrating in and perpendicular to the plane of the paper. The former is the E ray in the left half of the Babinet compensator and the latter is the O ray. In the right half the nomenclature is the opposite. In the compensator the two components acquire a pahse difference which depends on the relative position of the ray. If the ray is incident at a distance x above the central line through the compensator then the E ray acquires a phase
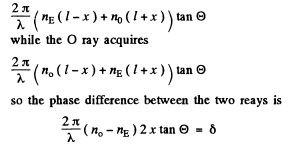
we get dark fringes when ever 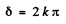
because then the emergent light is the same as that coming from the polarizer and is quenched by the analyser. 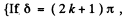 we get bright fringes because in this case, the plane of polarizaton of the emergent hight has rotated by 90° and is therefore fully transmitted by the analyser.} If follows that the fringe width
we get bright fringes because in this case, the plane of polarizaton of the emergent hight has rotated by 90° and is therefore fully transmitted by the analyser.} If follows that the fringe width
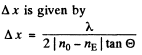
(b) If the fringes are displaced upwards by δx, then the path difference introduced by the sample between the O and the E rays must be such as to be exactly cancelled by the compensator. Thus
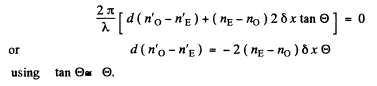
Q.189. Using the tables of the Appendix, calculate the difference of refractive indices of quartz for light of wavelength λ = 589.5 nm with right-hand and left-hand circular polarizations.
Ans. Light polarized along the x-direction (i.e. one whose electric vector has only an x component) and propagating along the z-direction can be decomposed into left and right circularly polarized light in accordance with the formula
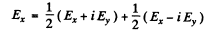
On passing through a distance l of an active medium these acquire the phases 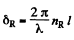
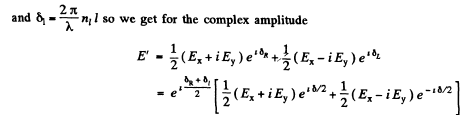

Apart from an over all phase 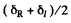 (which is irrelevant) this represents a wave whose plane of polarization has rotated by
(which is irrelevant) this represents a wave whose plane of polarization has rotated by
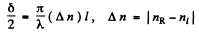
By definition this equals αl so
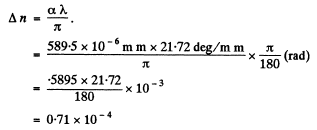
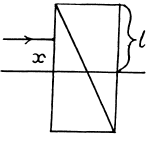
Q.190. Plane-polarized light of wavelength 0.59 tun falls on a trihedral quartz prism P (Fig. 5.34) with refracting angle 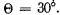 . Inside the prism light propagates along the optical axis whose direction is shown by hatching.
. Inside the prism light propagates along the optical axis whose direction is shown by hatching.
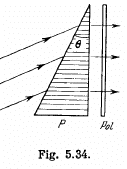
Behind the Polaroid Pol an interference pattern of bright and dark fringes of width Δx = = 15.0 mm is observed. Find the specific rotation constant of quartz and the distribution of intensity of light behind the Polaroid.
Ans. Plane polarized light on entering the wedge decomposes into right and left circularly polarized light which travel with different speeds in P and the emergent light gets its plane of polarization rotated by an angle which depends on the distance travelled.
Given that Δ x = fringe width

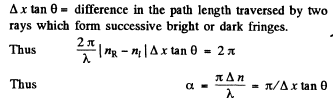
Let x = distance on the polaroid Pol as measured from a maximum. Then a ray that falls at this distance traverses an extra distance equal to

Q.191. Natural monochromatic light falls on a system of two crossed Nicol prisms between which a quartz plate cut at right angles to its optical axis is inserted. Find
the minimum thickness of the plate at which this system will transmit η = 0.30 of luminous flux if the specific rotation constant of quartz is equal to α= 17 ang.deg/mm.
Ans. If l0 intensity of natural light then
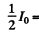 intensity of light emerging from the polarizer nicol.
intensity of light emerging from the polarizer nicol.
Suppose the quartz plate rotates this light by φ, then the analyser will transmit


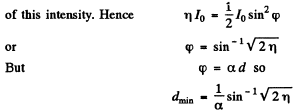

Q.192. Light passes through a system of two crossed Nicol prisms between which a quartz plate cut at right angles to its optical axis is placed. Determine the minimum thickness of the plate which allows light of wavelength 436 nm to be completely cut off by the system and transmits half the light of wavelength 497 nm. The specific rotation constant of quartz for these wavelengths is equal to 41.5 and 31.1 angular degrees per mm respectively.
Ans. For light of wavelength 436 nm
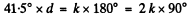
(Light will be completely cut off when the quartz plate rotates the plane of polarization by a multiple of 180°.) Here d = thickness of quartz plate in mm.
For natural incident light, half the light will be transmitted when the quartz rotates light by an odd multiple of 90°. Thus
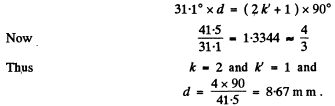
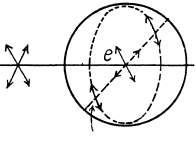
Q.193. Plane-polarized light of wavelength 589 nm propagates along the axis of a cylindrical glass vessel filled with slightly turbid sugar solution of concentration 500 g/l. Viewing from the side, one can see a system of helical fringes, with 50 cm between neighbouring dark fringes along the axis. Explain the emergence of the fringes and determine the specific rotation constant of the solution.
Ans. Two effects are involved here : rotation of plane of polarizatin by sugar solution and the effect of that rotation on the scattering of light in the transverse direction. The latter is shown in the figure given below. It is easy to see trom the figure that there will be no scattering of light in this transverse direction if the incident light has its electric vector parallel to the line of sight. In such a situation, we expect fringes to occur in the given experiment.
From the given data we see that in a distance of 50 cm, the rotation of plane of polarization must be 180°. Thus the specific rotation constant of sugar
Q.194. A Kerr cell is positioned between two crossed Nicol prisms so that the direction of electric field E in the capacitor forms an angle of 45° with the principal directions of the prisms. The capacitor has the length l = 10 cm and is filled up with nitrobenzene. Light of wavelength λ = 0.50 [tm passes through the system. Taking into account that in this case the Kerr constant is equal to B = 2.2.10-10 cm/V2, find:
(a) the minimum strength of electric field E in the capacitor at which the intensity of light that passes through this system is independent of rotation of the rear prism;
(b) how many times per second light will be interrupted when a sinusoidal voltage of frequency v = 10 MHz and strength amplitude Em = 5 0 kV/cm is applied to the capacitor.
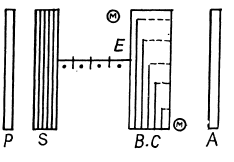
Note. The Kerr constant is the coefficient B in the equation ne - no = BλE2.
Ans. (a) in passing through the Kerr cell the two perpendicular components of the electric field will acquire a phase difference. When this phase difference equals 90° the emergent light will be circularly polarized because the two perpendicular components O & E have the same magnitude since it is given that the direction of electric field E in the capacitor forms an angle of 45° with the principal directions of then icols. In this case the intensity of light that emerges from this system will be independent of the rotation of the analyser prism.
Now the phase difference introduced is given by
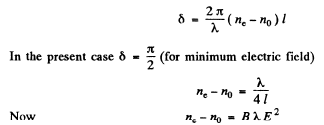
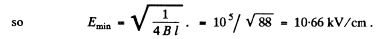
(b) If the applied electric field is
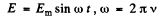
than the Kerr cell introduces a time varying phase difference
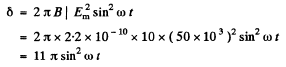
In one half-cycle 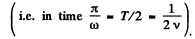
this reaches the value 2kπ when
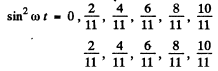
i.e. 11 times. On each of these occasions light will be interrupted. Thus light will be interrupted
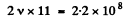 times per second
times per second
(Light will be interrupted when the Kerr cell (placed between crossed Nicols) introduces a phase difference oil kit and in no other case .)
Q.195. Monochromatic plane-polarized light with angular frequency ω passes through a certain substance along a uniform magnetic field H. Find the difference of refractive indices for right-hand and left-hand components of light beam with circular polarization if the Verdet constant is equal to V.
Ans. From problem 189, we know that
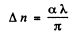
where α is the rotation constant Thus
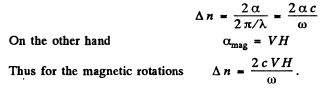
Q.196. A certain substance is placed in a longitudinal magnetic field of a solenoid located between two Polaroids. The length of the tube with substance is equal to l = 30 cm. Find the Verdet constant if at a field strength H = 56.5 kA/m the angle of rotation of polarization plane is equal to 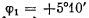 or one direction of the field and to
or one direction of the field and to 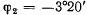 the opposite direction.
the opposite direction.
Ans. Part of the rotations is due to Faraday effect and part of it is ordinary optical rotation. The latter does not change sign when magnetic field is reversed. Thus
Hence 
or 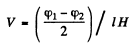
Putting the values 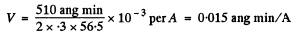
Q.197. A narrow beam of plane-polarized light passes through dextrorotatory positive compound placed into a longitudinal magnetic field as shown in Fig. 5.35. Find the angle through which the
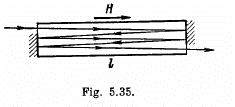
polarization plane of the transmitted beam will turn if the length of the tube with the compound is equal to 1, the specific rotation constant of the compound is equal to α, the Verdet constant is V, and the magnetic field strength is H.
Ans. We write
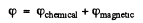
We look against the transmitted beam and count the positive direction clockwise. The chemical part of the rotation is annulled by reversal of wave vector up on reflection .
Thus
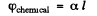
Since in effect there is a single transmission.
On the other hand
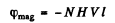
To get the signs right recall that dextro rotatory compounds rotate the plane of vibration in a clockwise direction on looking against the oncoming beam. The sense of rotation of light vibration in Faraday effect is defined in terms of the direction of the field, positive rotation being that of a right handed screw advancing in the direction of the field. This is the opposite of the definition of  for the present case. Finally
for the present case. Finally
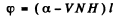
(Note : If plane polarized light is reflected back & forth through the same active medium in a magnetic Held, the Faraday rotation increases with each traveresal.)
Q.198. A tube of length l = 26 cm is filled with benzene and placed in a longitudinal magnetic field of a solenoid positioned between two Polaroids. The angle between the principle directions of the Polaroids is equal to 45°. Find the minimum strength of the magnetic field at which light of the wavelength 589 nm propagates through that system only in one direction (optical valve). What happens if the direction of the given magnetic field is changed to the opposite one?
Ans. There must be a Faraday rotation by 45° in through the second polaroid. Thus
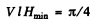
or
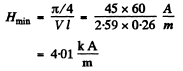
If the direction of magnetic field is changed then the sense of rotation will also change. Light will be completely quenched in the above case.
Q.199. Experience shows that a body irradiated with light with circular polarization acquires a torque. This happens because such a light possesses an angular momentum whose flow density in vacuum is equal to M = l/ω, where I is the intensity of light, ω is the angular oscillation frequency. Suppose light with circular polarization and wavelength λ = 0.70 lam falls normally on a uniform black disc of mass m = 10 mg which can freely rotate about its axis. How soon will its angular velocity become equal to ωo = = 1.0 rad/s provided I = 10 W/cm2?
Ans. Let r - radius of the disc
then its moment of inertia about its axis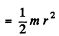
In time t the disc will acquire an angular momentum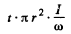
when circularly polarized light of intensity l falls on it. By conservation of angular momentum this must equal
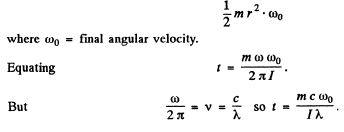
Substituting the values of the various quantities we get
t = 11.9 hours
FAQs on Irodov Solutions: Polarization of Light- 3 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is polarization of light? |  |
| 2. How does polarization occur in light? |  |
| 3. What are the types of polarization? |  |
| 4. How is polarization of light used in everyday life? |  |
| 5. Can unpolarized light become polarized? |  |

|
Explore Courses for JEE exam
|

|

















