Irodov Solutions: Properties of Atoms. Spectra- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.97. The binding energy of a valence electron in a Li atom in the states 2S and 2P is equal to 5.39 and 3.54 eV respectively. Find the Rydberg corrections for S and P terms of the atom.
Ans. From ihe Rydbeig formula we write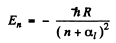
we use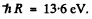 
Then for n = 2 state
α1 = -0.41
for p state
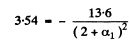
α1 = -0.039
Q.98. Find the Rydberg correction for the 3P term of a Na atom whose first excitation potential is 2.10 V and whose valence electron in the normal 3S state has the binding energy 5.14 eV.
Ans. The energy of the 3p state must be -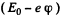 
where - E0 is the energy of the 3S state.
Then
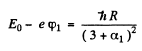
so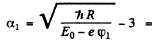 
Q.99. Find the binding energy of a valence electron in the ground state of a Li atom if the wavelength of the first line of the sharp series is known to be equal to λ1 = 813 nm and the short-wave cutoff wavelength of that series to λ2 = 350 nm.
Ans. For the first line of the sharp series 
in a Li atom
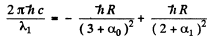
For the short wave cut-off wave-length of the same series
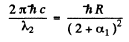
From these two equations we get on subtraction
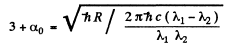
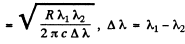
Thus in the ground state, the binding energy of the electron is
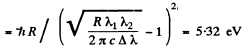
Q.100. Determine the wavelengths of spectral lines appearing on transition of excited Li atoms from the state 3S down to the ground state 2S. The Rydberg corrections for the S and P terms are —0.41 and —0.04.
Ans. The energy of the 3 S state is
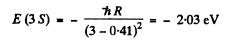
The energy of a 2 S state is
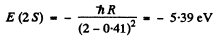
The energy of a 2 P state is
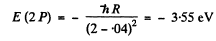
We see that
E (2S ) <E (2P)< E ( 3 S)
The transitions are 3S → 2P and 2P →2S.
Direct 3S → 2S transition is forbidden by selection rules. The wavelengths are determined by
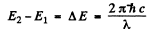
Substitution gives
λ = 0.816 μm ( 3S → 2P )
and λ = 0.674 μm ( 2P → 2S )
Q.101. The wavelengths of the yellow doublet components of the resonance Na line caused by the transition 3P → 3S are equal to 589.00 and 589.56 nm. Find the splitting of the 3P term in eV units.
Ans. The splitting of the Na lines is due to the fine structure splitting of 3 p lines (The 3 s state is nearly single except for possible hyperfine effects.) The splitting of the 3 p level then equals the energy difference
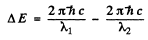
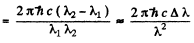
Here Δλ = wavelength difference & λ = average wavelength. Substitution gives
ΔE = 2.0 meV
Q.102. The first line of the sharp series of atomic cesium is a doublet with wavelengths 1358.8 and 1469.5 nm. Find the frequency intervals (in rad/s units) between the components of the sequent lines of that series.
Ans. The sharp series arise from the transitions ns → mp . The s lines are unsplit so the splitting is due entirely to the p level. The frequency difference between sequent lines is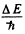 
and is the same for all lines of the sharp series. It is
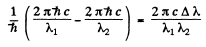
Evaluation gives
1.645 x 1014 rad/s
Q.103. Write the spectral designations of the terms of the hydrogen atom whose electron is in the state with principal quantum number n = 3.
Ans. We shall ignore hyperfine interaction. The state with principal quantum number n = 3 has orbital angular momentum quantum number
/ = 0, 1,2
The levels with these terms are 3 5 , 3 P, 3 D. The total angular momentum is obtained by combining spin and angular momentum. For a single electron this leads to
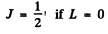
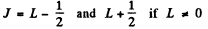
We then get the final designations
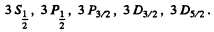
Q.104. How many and which values of the quantum number J can an atom possess in the state with quantum numbers S and L equal respectively to
(a) 2 and 3;
(b) 3 and 3;
(c) 5/2 and 2?
Ans. The rule is that if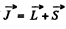 
then J takes the values
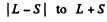
in step of 1. Thus :
(a) The values are 1, 2, 3, 4, 5
(b) The values are 0, 1, 2, 3, 4, 5, 6
(c) The values are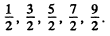 
Q.105. Find the possible values of total angular momenta of atoms in the states 4P and 6D.
Ans. For the state 4 p, L = 1, S =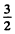 
( since 2s + 1 = 4 ) . For the state 5 d , Z , = 2 , s = 2 .
The possible values of J are
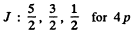
The value of the magnitude of angular momentum is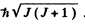 
Substitution gives the values
4 P :
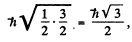
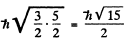
and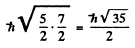 
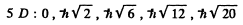
Q.106. Find the greatest possible total angular momentum and the corresponding spectral designation of the term
(a) of a Na atom whose valence electron possesses the principal quantum number n = 4;
(b) of an atom with electronic configuration 1s22p3d.
Ans. (a) For the Na atoms the valence electron has principal quantem number n = 4, and the possible values of orbital angular momentum are l = 0 , 1, 2 , 3 so lmax = 3 . The state is 2F, maximum value of J is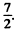 
Thus the state with maximum angular momentum will be
For this state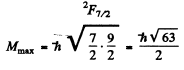 
(b) For the atom with electronic configuration 1 s2 2 p 3 d . There are two inequivalent valence electrons. The total orbital angular moments will be 1, 2, 3 so we pick l = 3. The total spin angular momentum will be s = 0, 1 so we pick up s = 1. Finally 7 will be 2, 3 , 4 so we pick up 4. Thus maximum angular momentum state is
For this state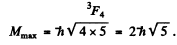 
Q.107. It is known that in F and D states the number of possible values of the quantum number J is the same and equal to five. Find the spin angular momentum in these states.
Ans. For the f state L = 3 , For the d state L = 2. Now if the state has spin s the possible angular momentum are
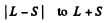
The number of J angular momentum values i s 2 S + 1 if L ≥ S and 2 L + 1 if L < S. Since the number of states is 5 , we must have S ≥ L = 2 for D state while S ≤ 3 and 2 S + 1 = 5 in ply S = 2 for F state. Thus for the F state total spin angular momentum
while for D state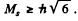 
Q.108. An atom is in the state whose multiplicity is three and the total angular momentum is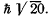 
What can the corresponding quantum number L be equal to?
Ans. Multiplicity is 2S + l so S = 1 .
Total angular m om entum is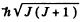 
so J = 4. Then
L must equal 3, 4, 5
in order that J = 4 may be included in
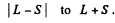
Q.109. Find the possible multiplicities x of the terms of the types (a) xD2; (b) xHP3/2; (c) xF1.
Ans. (a) Here J = 2, L = 2. Then S = 0, 1 , 2, 3, 4
and the multiplicities( 2S - 1 ) are
1, 3, 5, 7, 9.
(b) Here J = 3 / 2 , L = 1 Then
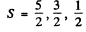and the multiplicities are 6, 4, 2
(c) Here J = 1, L = 3. Then S = 2 , 3 , 4
and the multiplicities are 5, 7, 9
Q.110. A certain atom has three electrons (s, p, and d), in addition to filled shells, and is in a state with the greatest possible total mechanical moment for a given configuration. In the corresponding vector model of the atom find the angle between the spin momentum and the total angular momentum of the given atom.
Ans. The total angular momentum is greatest when L, S are both greatest and add to form J. Now for a triplet of s, p> d electrons Maximum spin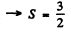
corresponding to
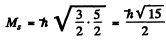
Maximum oibital angular momentum → L = 3
corresponding to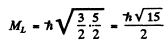 
Maximum total angular momentum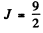 
corresponding to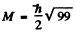 
In vector model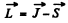 
or in magnitude squared
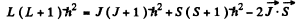
Thus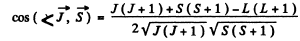 
Substitution gives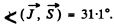 
Q.111. An atom possessing the total angular momentum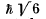 
is in the state with spin quantum number S = 1. In the corresponding vector model the angle between the spin momentum and the total angular momentum is θ = 73.2°. Write the spectral symbol for the term of that state.
Ans. Total angular momentum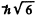 
means J = 2. It is gives that S = 1.
This means that L = 1,2, or 3 . From vector model relation
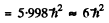
Thus E = 2 and the spectral symbol of the state is
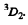
Q.112. Write the spectral symbols for the terms of a two-electron system consisting of one p electron and one d electron.
Ans. In a system containing a p electron and a d electron
S = 0,1
L = 1,2,3
For S = 0 we have the terms
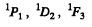
For S = 1 we have the terms
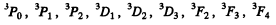
Q.113. A system comprises an atom in 2P3/2 state and a d electron. Find the possible spectral terms of that system.
Ans. The atom has
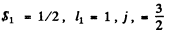
The electron has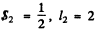 
so the total angular momentum quantum number must be
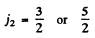
In L - S compling we get S = 0, 1 . L = 1 ,2 , 3 and the terms that can be formed are the same as written in the problem above. The possible values of angular momentum are consistant
with the addition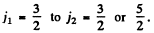 
The latter gives us J = 0, 1, 2, 3 ; 1, 2, 3, 4
All these values are reached above.
Q.114. Find out which of the following transitions are forbidden by the selection rules: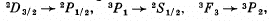 
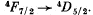
Ans. Selection rules are ΔS = 0
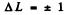
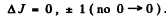
Thus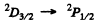 
is allowed
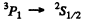not allowed
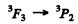is not allowed (ΔL = 2)
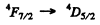is allowed
Q.115. Determine the overall degeneracy of a 3D state of a Li atom. What is the physical meaning of that value?
Ans. For a 3 d state of a Li atom,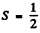 
because there is only one electron and L = 2.
The total degeneracy is
g = (2L + 1) (2S + 1) = 5 x 2 = 10.
The states are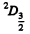 
and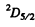 
and we check that
g = 4 + 6 =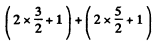
FAQs on Irodov Solutions: Properties of Atoms. Spectra- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are the properties of atoms? |  |
| 2. What is the significance of atomic spectra? | |
| 3. How are atomic spectra produced? | |
| 4. What is the relationship between atomic spectra and electron configuration? | |
| 5. How are atomic spectra used in practical applications? | |
