Irodov Solutions: Properties of Atoms. Spectra- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.116. Find the degeneracy of the states 2P, 3D, and 4F possessing the greatest possible values of the total angular momentum.
Ans. The state with greatest possible total angular momentum are
For a 2P state 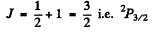
Its degeneracy is 4.
For a 3D state 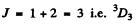
Its degeneracy is 2 x 3 + 1 = 7
For a 4F state 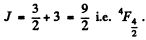
Its degeneracy is 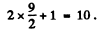
Q.117. Write the spectral designation of the term whose degeneracy is equal to seven and the quantum numbers L and S are interrelated as L = 3S.
Ans. The degeneracy is 2J + 1. So we must have J = 3. From L = 3 S, we see that S must be an integer since L is integral and S can be either integral or half integral. If S = 0 then L = 0 but this is consistent with J = 3. For S ≥ 2, L ≥ 6 and then J = 3. Thus the state is
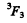
Q.118. What element has the atom whose K, L, and M shells and 4s subshell are filled completely and 4p subshell is half-filled?
Ans. The order of filling is
K , L , M shells, then 4 s2 , 3d10 then 4p3. The electronic configuration of the element will be
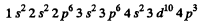
(There must be three 4p electrons)
The number of electrons is 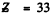 and the element is As. (The 3d subshell must be filled before 4p fills up.)
and the element is As. (The 3d subshell must be filled before 4p fills up.)
Q.119. Using the Hund rules, find the basic term of the atom whose partially filled subshell contains (a) three p electrons; (b) four p electrons.
Ans. (a) when the partially filled shell contains three p electrons, the total spin S must equal
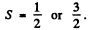 The state
The state 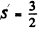 has maximum spin and is totalIy symmetric under exchange of spin lables. By Pauli’s exclusion principle this implies that the angular part of the wavefunction must be totally anti symmetric. Since the angular part of the wave function a p electron is
has maximum spin and is totalIy symmetric under exchange of spin lables. By Pauli’s exclusion principle this implies that the angular part of the wavefunction must be totally anti symmetric. Since the angular part of the wave function a p electron is 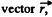 the total wavefunction of three p electrons is the totally antisymmetric combination
the total wavefunction of three p electrons is the totally antisymmetric combination 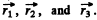 The only such combination is
The only such combination is
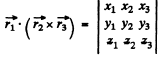
This combination is a scalar and hence has L = 0. The spectral term of the ground state is then
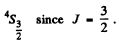
(b) We can think of four p electrons as consisting of a full p shell with two p holes. The state of maximum spin S is then S = 1. By Pauli’s principle the orbital angular momentum part must be antisymmetric and can only have the form
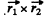
where 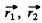 are the coordinates of holes. The result is harder to see if we do not use the concept of holes. Four p electrons can have S = 0, 1, 2 but the S = 2 state is totally symmetric. The corresponding angular wavefunction must be totally antisymmetric. But this is impossible : there is no quantity which is amtisymmetric in four vectors. Thus the maximum allowed S is S = 1. We can construct such a state by coupling the spins of electrons 1 & 2 to 5 = 1 and of electrons 3 & 4 to S = 1 and then coupling the resultant spin states to S = 1. Such a state is symmetric under the exchange of spins of 1 & 2nd 3 and 4 but antisymmetric under the simultaneous exchange of (1, 2) & (3, 4). the conjugate angular wavefimction must be antisymmetric under the exchange of (1, 2) and under the exchange of (3, 4) by Pauli principle. It must also be antisymmetric under the simultaneous exchange of (1, 2) and (3, 4). (This is because two exchanges of electrons are involved.) The required angular wavefunction then has the form
are the coordinates of holes. The result is harder to see if we do not use the concept of holes. Four p electrons can have S = 0, 1, 2 but the S = 2 state is totally symmetric. The corresponding angular wavefunction must be totally antisymmetric. But this is impossible : there is no quantity which is amtisymmetric in four vectors. Thus the maximum allowed S is S = 1. We can construct such a state by coupling the spins of electrons 1 & 2 to 5 = 1 and of electrons 3 & 4 to S = 1 and then coupling the resultant spin states to S = 1. Such a state is symmetric under the exchange of spins of 1 & 2nd 3 and 4 but antisymmetric under the simultaneous exchange of (1, 2) & (3, 4). the conjugate angular wavefimction must be antisymmetric under the exchange of (1, 2) and under the exchange of (3, 4) by Pauli principle. It must also be antisymmetric under the simultaneous exchange of (1, 2) and (3, 4). (This is because two exchanges of electrons are involved.) The required angular wavefunction then has the form
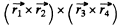
and is a vector, L = 1 . Thus, using also the fact that the shell is more than half full, we find the spectral term 3P2
( J = L + S ) .
Q.120. Using the Hund rules, find the total angular momentum of the atom in the ground state whose partially filled subshell contains (a) three d electrons; (b) seven d electrons.
Ans. (a) The maximum spin angular momentum of three electrons can be 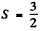 . This state is totally symmetric and hence the conjugate angular wavefunction must be antisymmetric By Pauli’s exclusion principle the totally antisymmetric state must have different magnetic quantum numbers. It is easy to see that for d electrons the maximum value of the magnetic quantum number for oibital angular momentum
. This state is totally symmetric and hence the conjugate angular wavefunction must be antisymmetric By Pauli’s exclusion principle the totally antisymmetric state must have different magnetic quantum numbers. It is easy to see that for d electrons the maximum value of the magnetic quantum number for oibital angular momentum 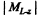 = 3 (from 2 + 1 + 0). Higher values violate Pauli’s principle. Thus the state of highest orbital angular momentum consistent with Pauli’s principle is L = 3.
= 3 (from 2 + 1 + 0). Higher values violate Pauli’s principle. Thus the state of highest orbital angular momentum consistent with Pauli’s principle is L = 3.
The state of the atom is then 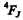 where J = L - S by H und’s rule. Thus we get
where J = L - S by H und’s rule. Thus we get
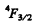
The magnitude of the angular momentum is
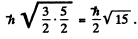
(b) Seven d electrons mean three holes. Then 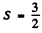 and L = 3 as before. But
and L = 3 as before. But
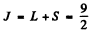 by Hund’s rule for more than half filled shell. Thus the state is
by Hund’s rule for more than half filled shell. Thus the state is
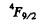
Total angular momentum has the magnitude
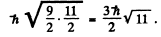
Q.121. Making use of the Hund rules, find the number of electrons in the only partially filled subshell of the atom whose basic term is (a) 3F2; (b) 2P3/2; (c) 6S5/2.
Ans. (a) 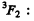 The maximum value of spin is S = 1 here. This means there are 2 electrons.
The maximum value of spin is S = 1 here. This means there are 2 electrons.
L - 3 so s and p electrons are ruled out. Thus the simplest possibility is d electrons. This is the correct choice for if we were considering f electrons, the maximum value of L allowed by Pauli principle will be L = 5 (maximum value of the magnitude of magnetic quantum number will be 3 + 2 - 5 .)
Thus the atom has two d electrons in the unfilled shell.
(b) 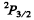 Here
Here 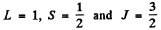
Since J = L + S, Hund’s rule im plies the shell is more than halffull. This means one electron less than a full shell. On the basis of hole picture it is easy to see that we have p electrons. Thus the atom has 5 p electrons.
(c)  Here
Here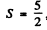 L = 0 . We either have five electrons or five holes. The angular part is antisymmetric. For five d electrons, the maximum value of the quantum number consistent with Pauli exclusion principle is ( 2 + l + 0 - l - 2 ) = 0 so L = 0 . For f or g electrons L > 0 whether the shell has five electrons or five holes. Thus the atom has five d electrons.
L = 0 . We either have five electrons or five holes. The angular part is antisymmetric. For five d electrons, the maximum value of the quantum number consistent with Pauli exclusion principle is ( 2 + l + 0 - l - 2 ) = 0 so L = 0 . For f or g electrons L > 0 whether the shell has five electrons or five holes. Thus the atom has five d electrons.
Q.122. Using the Hund rules, write the spectral symbol of the basic term of the atom whose only partially filled subshell (a) is filled by 1/3, and S = 1; (b) is filled by 70%, and S = 3/2.
Ans. (a) If S = 1 is the maximum spin then there must be two electrons (If there are two holes then the shell will be more than half full.). This means that there are 6 electrons in the full shell so it is a p shell. By Paul’s principle the only antisymmetric combination of two electrons has L = 1 Also J = L - S as the shell is less than half full. Thus the term is 3P0
(b) 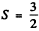 means either 3 electrons or 3 holes. As the shell is more than half full the former possibility is ruled out. Thus we must have seven d electrons. Then as in problem 6.120 we get the term
means either 3 electrons or 3 holes. As the shell is more than half full the former possibility is ruled out. Thus we must have seven d electrons. Then as in problem 6.120 we get the term 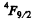
Q.123. The only partially filled subshell of a certain atom contains three electrons, the basic term of the atom having L = 3. Using the Hund rules, write the spectral symbol of the ground state of the given atom.
Ans. With three electrons 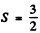 and the spin part is totally symmetric. It is given that the basic term has L = 3 so L = 3 is the state o f highest orbital angular momentum. This is not possible with p electron so we must have d electrons for which L = 3 for 3 electrons. For three f, g electrons L > 3. Thus we have 3 d electrons. Then as in (6.120) the ground state is
and the spin part is totally symmetric. It is given that the basic term has L = 3 so L = 3 is the state o f highest orbital angular momentum. This is not possible with p electron so we must have d electrons for which L = 3 for 3 electrons. For three f, g electrons L > 3. Thus we have 3 d electrons. Then as in (6.120) the ground state is
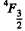
Q.124. Using the Hund rules, find the magnetic moment of the ground state of the atom whose open subshell is half-filled with five electrons.
Ans. We have 5d electrons in the only unfilled shell. Then 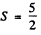 aximum value of L consistent with Pauli’s principle is L = 0. Then
aximum value of L consistent with Pauli’s principle is L = 0. Then
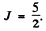
So by Lande’s formula
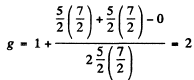
Thus 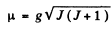
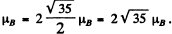
The ground state is 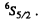
Q.125. What fraction of hydrogen atoms .is in the state with the principal quantum number n = 2 at a temperature T = 3000 K?
Ans. By Boltzmann formula

Here ΔE = energy difference between n = 1 and n = 2 states
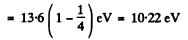
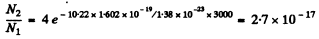
Explicitly 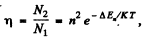
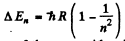
for the nth excited state because the degeneracy of the state with principal quantum number n is 2 n2.
Q.126. Find the ratio of the number of atoms of gaseous sodium in the state 3P to that in the ground state 3S at a temperature T 2400 K. The spectral line corresponding to the transition 3P → 3S is known to have the wavelength λ = 589 nm.
Ans. We have
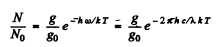
Here g = degeneracy ofthe 3P sate = 6, g0 = degeneracy of the 3S state = 2 and λ wavelength of the 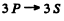 line
line 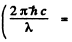 energy difference between 3P & 3S levels.
energy difference between 3P & 3S levels.
Substitution gives 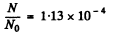
Q.127. Calculate the mean lifetime of excited atoms if it is known that the intensity of the spectral line appearing due to transition to the ground state diminishes by a factor η = 25 over a distance l = 2.5 mm along the stream of atoms whose velocity is v = = 600 m/s.
Ans. Let T = mean life time o f the excited atoms. Then the number o f excited atoms will decrease with time as 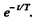 In time t the atom travels a distance vt so
In time t the atom travels a distance vt so 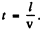 Thus the number of excited atoms in a beam that has traversed a distance l has decreased by
Thus the number of excited atoms in a beam that has traversed a distance l has decreased by
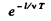
The intensity of the line is proportional to the number of excited atoms in the, beam. Thus
 = 1.29 x 10-6 second.
= 1.29 x 10-6 second.
Q.128. Rarefied Hg gas whose atoms are practically all in the ground state was lighted by a mercury lamp emitting a resonance line of wavelength λ = 253.65 nm. As a result, the radiation power of Hg gas at that wavelength turned out to be P = 35 mW. Find the number of atoms in the state of resonance excitation whose mean lifetime is ζ = 0.15μs.
Ans. As a result of the lighting by the mercury lamp a number of atoms are pumped to the excited state. In equilibrium the number of such atoms is N. Since the mean life time of the atom is T, the number decaying per unit time is 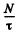 Since a photon of energy
Since a photon of energy 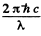 results from each decay, the total radiated power will be
results from each decay, the total radiated power will be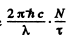 . This must equal P. Thus
. This must equal P. Thus
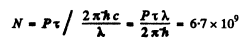
Q.129. Atomic lithium of concentration n = 3.6.1016 cm-3 is at a temperature T = 1500 K. In this case the power emitted at the resonant line's wavelength λ = 671 nm (2P → 2S) per unit volume of gas is equal to P = 0.30 W/cm3. Find the mean lifetime of Li atoms in the resonance excitation state.
Ans. The number of excited atoms per unit volume of the gas in 2P state is
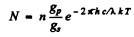
Here gp = degeneracy of the 2p state = 6, gr = degeneacy of the 2s state = 2 and λ = wavelength of the resonant line 2 p → 2 s . The rate of decay of these atoms is 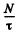 per sec. per unit volume. Since each such atom emits light of wavelength X, we must have
per sec. per unit volume. Since each such atom emits light of wavelength X, we must have
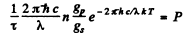
Thus 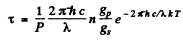
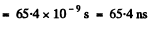
Q.130. Atomic hydrogen is in thermodynamic equilibrium with its radiation. Find: (a) the ratio of probabilities of induced and spontaneous radiations of the atoms from the level 2P at a temperature T = 3000 K; (b) the temperature at which these probabilities become equal.
Ans. (a) We know that
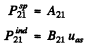
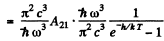
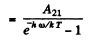
Thus 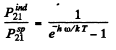
For the transition 2P→1S 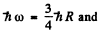
we get 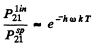
substitution gives 7 x 10-18
(b) The two rates become equal when 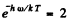
or
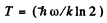 = 1.71 x 105 K
= 1.71 x 105 K
FAQs on Irodov Solutions: Properties of Atoms. Spectra- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are the properties of atoms mentioned in Irodov Solutions: Properties of Atoms. Spectra- 2? |  |
| 2. How is electron configuration defined in the context of atoms? |  |
| 3. What is atomic size and how does it vary across the periodic table? |  |
| 4. What is ionization energy and why is it an important property of atoms? |  |
| 5. How does electronegativity influence the chemical behavior of atoms? |  |

|
Explore Courses for JEE exam
|

|

















