Irodov Solutions: Properties of Atoms. Spectra- 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.131. A beam of light of frequency ω, equal to the resonant frequency of transition of atoms of gas, passes through that gas heated to temperature T. In this case hω >> kT. Taking into account induced radiation, demonstrate that the absorption coefficient of the gas x varies as x = xo (1. — e -hω/kT), where xo is the absorption coefficient for T0.
Ans. Because of the resonant nature of the processes we can ignore nonresonant processes. We also ignore spontaneous emission since it does not contribute to the absorption coefficient and is a small term if the beam is intense enough.
Suppose I is the intensity of the beam at some point. The decrease in the value of this intensity on passing through the layer of the substance of thickness d x is equal to
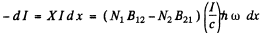
Here N1 = No. of atoms in lower level
N2 = No of atoms in the upper level per unit volume.
B12 , B21 are E in stein coefficients and
Ic = energy density in the beam ,
c = velocity of light
A factor 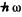 arises because each transition result in a loss or gain of energy
arises because each transition result in a loss or gain of energy 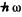
Hence 
But g1B12 = g2B21 so

By Boltzman factor 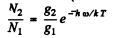
When 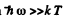 we can put N1= N0 the total number of atoms per unit volume.
we can put N1= N0 the total number of atoms per unit volume.
Then 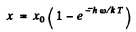
where 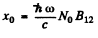 is the absorption coefficient for T → 0.
is the absorption coefficient for T → 0.
Q.132. The wavelength of a resonant mercury line is λ = = 253.65 nm. The mean lifetime of mercury atoms in the state of resonance excitation is ζ = 0.15 μs. Evaluate the ratio of the Doppler line broadening to the natural linewidth at a gas temperature T = 300 K.
Ans. A short lived state of mean life T has an uncertainty in energy of 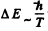 which is transmitted to the photon it emits as natural broadening. Then
which is transmitted to the photon it emits as natural broadening. Then
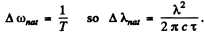
The Doppler broadening on the other hand arises from the thermal motion of radiating atoms.
The effect is non-relativistic and the maximum broadening can be written as
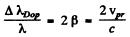
Thus 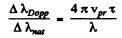
Substitution gives using 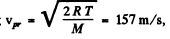
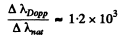
Note: Our formula is an order of magnitude estimate.
Q.133. Find the wavelength of the Kα line in copper (Z = 29) if the wavelength of the Kα line in iron (Z = 26) is known to be equal to 193 pm.
Ans. From Moseley’s law
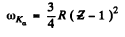
or 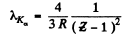
Thus 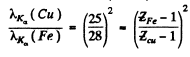
Substitution gives
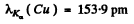
Q.134. Proceeding from Moseley's law find:
(a) the wavelength of the Kα line in aluminium and cobalt:
(b) the difference in binding energies of K and L electrons in vanadium.
Ans. (a) From Moseley’s law
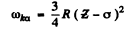
or 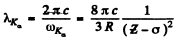
We shall take σ = 1. For Aluminium 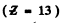
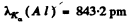
and for cobalt (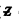 = 27)
= 27)
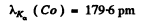
(b) This difference is nearly equal to the energy of the Kα line which by Moseley’s law is equal to (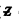 = 23 for vanadium)
= 23 for vanadium)
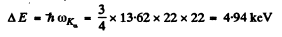
Q.135. How many elements are there in a row between those whose wavelengths of Kα lines are equal to 250 and 179 pm?
Ans. We calculate the 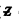 values corresponding to the given wavelengths using Moseley’s law. See problem (134).
values corresponding to the given wavelengths using Moseley’s law. See problem (134).
Substitution gives that
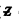 = 23 corresponding to λ = 250 pm
= 23 corresponding to λ = 250 pm
and 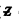 = 27 corresponding to λ = 179 pm
= 27 corresponding to λ = 179 pm
There are thus three elements in a row between those whose wavelengths of Kα lines are equal to 250 pm and 179 pm.
Q.136. Find the voltage applied to an X-ray tube with nickel anticathode if the wavelength difference between the Kα line and the short-wave cut-off of the continuous X-ray spectrum is equal to 84 pm.
Ans. From Moseley’s law
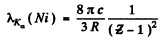
where 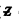 = 28 for Ni . Substitution gives
= 28 for Ni . Substitution gives
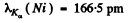
Now the short wave cut of off the continuous spectrum must be more energetic (smaller wavelength) otherwise Kα lines will not emerge. Then since 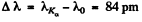 we get
we get
λ = 82.5 pm
This corresponds to a voltage of
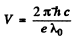
Substitution gives V = 15.0 kV
Q.137. At a certain voltage applied to an X-ray tube with aluminium anticathode the short-wave cut-off wavelength of the continuous X-ray spectrum is equal to 0.50 nm. Will the K series of the characteristic spectrum whose excitation potential is equal to 1.56 kV be also observed in this case?
Ans. Since the short wavelength cut off of the continuous spectrum is
λo = 0.50nm
the voltage applied m ust be 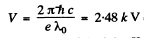
since this is greater than the excitation potential of the K series of the characteristic spectrum (which is only 1.56 k V ) the latter will be observed.
Q.138. When the voltage applied to an X-ray tube increased from V1 =10kV to V2 = 20 kV, the wavelength interval between the Kα line and the short-wave cut-off of the continuous X-ray spectrum increases by a factor n = 3.0. Find the atomic number of the element of which the tube's anticathode is made.
Ans. Suppose λo = wavelength of the characteristic X-ray line. Then using the formula for short wavelength limit of continuous radiation
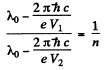
Hence 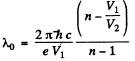
Using also Moseley’s law, we get
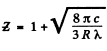
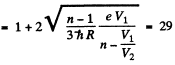
Q.139. What metal has in its absorption spectrum the difference between the frequencies of X-ray K and L absorption edges equal to Δω = 6.85.1018 s-1 ?
Ans. The difference in frequencies of the K and L absorption edges is equal, according to the Bohr picture, to the frequency of the Kα line (see the diagram below). Thus by Moseley’s formule
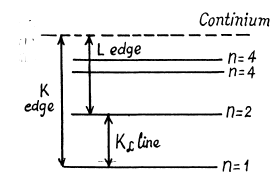

or
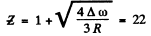
The metal is titanium,
Q.140. Calculate the binding energy of a K electron in vanadium whose L absorption edge has the wavelength λL = 2.4 nm.
Ans. From the diagram above w e see th at the binding energy Eb of a K electron is the sum o f the energy of a Kα line and the energy corresponding to the L edge of absorption spectrum
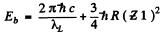
For vanadium 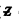 = 23 and the energy of Kα line of vanadium has been calculated in problem 134 (b). Using
= 23 and the energy of Kα line of vanadium has been calculated in problem 134 (b). Using
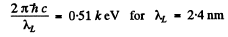
we get Eb = 5.46 k eV
Q.141. Find the binding energy of an L electron in titanium if the wavelength difference between the first line of the K series and its short-wave cut-off is Δλ = 26 pm.
Ans. By Moseley’s law
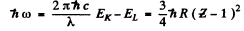
where - EK is the energy of the K electron and - EL of the L electron. Also the energy of the line corresponding to the short wave cut off of the K series is
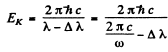
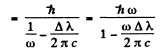
Hence 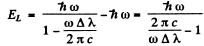
Substitution gives for titanium ( 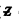 = 22)
= 22)
ω = 6.85 x 1018 s-1
and hence EL = 0.47keV
Q.142. Find the kinetic energy and the velocity of the photoelectrons liberated by Kα radiation of zinc from the K shell of iron whose K band absorption edge wavelength is λK = 174 pm.
Ans. The energy of the K a radiation of 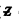 n is
n is
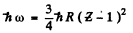
where E = atomic number of  zinc = 30. Th e binding energy of the K electrons in iron is obtained from the wavelength of K absorption edge as
zinc = 30. Th e binding energy of the K electrons in iron is obtained from the wavelength of K absorption edge as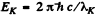 . Hence by Einstein equation
. Hence by Einstein equation
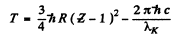
Substitution gives
T = 1.463 k eV
This corresponds to a velocity of the photo electrons of
v = 2.27x106m/s
Q.143. Calculate the Lande g factor for atoms (a) in S states; (b) in singlet states.
Ans. From the Lande formula
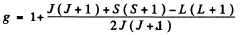
(a) For S states L = 0. This implies J = S. Then, if S = 0
g = 2
(For singlet states g is not defined if L = 0 )
(b) For singlet states, J = L
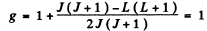
Q.144. Calculate the Lande g factor for the following terms: (a) 6F1/2; (b) 4D1/2; (c) 5F2; (d) 5P1; (e) 3Po.
Ans. (a) 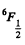 Here
Here 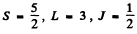
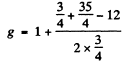
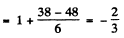
(b) 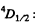 Here
Here 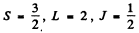
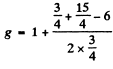
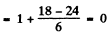
(c) 5F2 Here S = 2 , L = 3 , J = 2
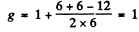
(d) 5P1 Here S = 2 , L = 1 , J = 1
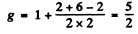
(e) 3P0. For states with J = 0, L = S the g gactor is indeterminate.
Q.145. Calculate the magnetic moment of an atom (in Bohr magnetons) (a) in 1F state; (b) in 2D3/2 state; (c) in the state in which S = 1, L = 2, and Lande factor g = 4/3.
Ans. (a) For the lF state S = 0, L = 3 = J
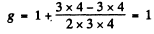
Hence 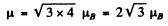
(b) For the 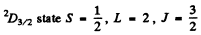
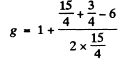
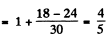
Hence 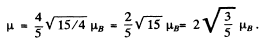
(c) We have 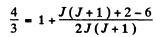
or 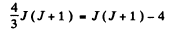
or 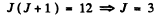
Hence 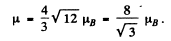
Q.146. Determine the spin angular momentum of an atom in the state D2 if the maximum value of the magnetic moment projection in that state is equal to four Bohr magnetons.
Ans. The expression for the projection of the magnetic moment is
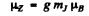
where mj is the projection of 
Maximum value of the mj is J. Thus
gJ = 4
Since J = 2 , we get g = 2. Now
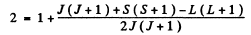
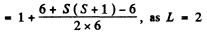

Hence S (S + 1) = 12 or S = 3
Thus 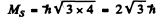
Q.147. An atom in the state with quantum numbers L = 2, S = 1. is located in a weak magnetic field. Find its magnetic moment if the least possible angle between the angular momentum and the field direction is known to be equal to 30°.
Ans. The angle between the angular momentum vector and the field direction is the least when the angular mommentum projection is maximum i.e. 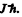
Thus 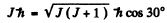
or 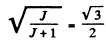
Hence J = 3
Then 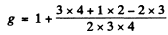
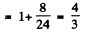
and 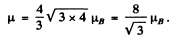
Q.148. A valence electron in a sodium atom is in the state with principal quantum number n = 3, with the total angular momentum being the greatest possible. What is its magnetic moment in that state?
Ans. For a state with n = 3 , l = 2. Thus the state with maximum angular momentum is
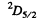
Then 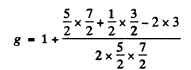
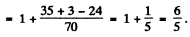
Hence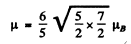
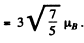

|
Explore Courses for JEE exam
|

|

















