Irodov Solutions: Properties of Atoms. Spectra- 4 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.149. An excited atom has the electronic configuration 1s22s22p3d being in the state with the greatest possible total angular momentum. Find the magnetic moment of the atom in that state.
Ans. To get the greatest possible angular momentum we must have S = Smax = 1
L = Lmax = 1 + 2 = 3 and J = L + S = 4
Then 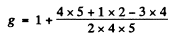
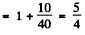
and 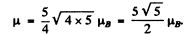
Q.150. Find the total angular momentum of an atom in the state with S = 3/2 and L = 2 if its magnetic moment is known to be equal to zero.
Ans. Since μ = 0 we must have either J = 0 or g = 0. But J = 0 is incompatible with L = 2 and S = 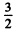 Hence g = 0. Thus
Hence g = 0. Thus
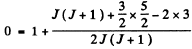
or 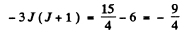
Hence 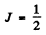
Thus 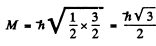
Q.151. A certain atom is in the state in which S = 2, the total angular momentum 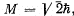 , and the magnetic moment is equal to zero. Write the spectral symbol of the corresponding term.
, and the magnetic moment is equal to zero. Write the spectral symbol of the corresponding term.
Ans. From 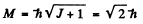
we find J = 1. From the zero value of the magnetic moment we find
g = o
or 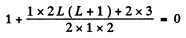
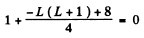
or 12 = L (L+ 1)
Hence L = 3 . The state is
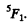
Q.152. An atom in the state 2P3/2 is located in the external magnetic field of induction B = 1.0 kG. In terms of the vector model find the angular precession velocity of the total angular momentum of that atom.
Ans. If  is the total angular momentum vector of the atom then there is a magnetic moment
is the total angular momentum vector of the atom then there is a magnetic moment
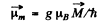
associated with it; here g is the Lande factor. In a magnetic field of induction 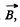 an energy
an energy
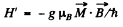
is associated with it. This interaction term corresponds to a presession of the angular momentum vector because if leads to an equation of motion of the angular momentum vector of the form
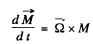
where 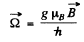
Using Gaussian unit expression of 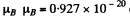 eig/gauss, B = 103 gauss
eig/gauss, B = 103 gauss
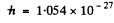 erg sec and for the 2P3/2 state
erg sec and for the 2P3/2 state
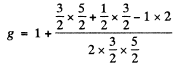
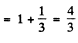
and Ω = 1.17 x 1010 rad/s
The same formula is valid in MKS units also But μB = 0.927 x 10 -23 A.m2 , B = 10-1 T and :h = 1.054 x 10-34 Joule sec. The answer is the same.
Q.153. An atom in the state 2P1/2 is located on the axis of a loop of radius r = 5 cm carrying a current I = 10 A. The distance between the atom and the centre of the loop is equal to the radius of the latter. How great may be the maximum force that the magnetic field of that current exerts on the atom?
The force on an atom with magnetic moment 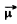 in a magnetic Geld of induction
in a magnetic Geld of induction 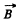 is given by
is given by
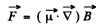
In the present case, the maximum force arise when 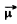 is along the axis or close to it.
is along the axis or close to it.
Then 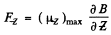
Here 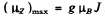 . The Lande factor g is for 2P1/2
. The Lande factor g is for 2P1/2
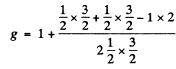
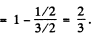
and 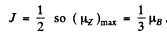
The magnetic field is given by
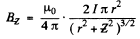
or 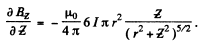
Thus 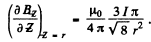
Thus the maximum force is
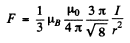
Substitution gives (using data in M K S units)
F = 4.1 x 10-27N
Q.154. A hydrogen atom in the normal state is located at a distance r = 2.5 cm from a long straight conductor carrying a current I = 10 A. Find the force acting on the atom.
Ans.The magnetic field at a distance r from a long current carrying wire is mostly tangential and given by
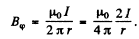
The force on a magnetic dipole of moment 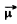 due to this magnetic field is also tangential and has a magnitude
due to this magnetic field is also tangential and has a magnitude
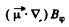
This force is nonvanishing only when the component of 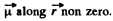 Then
Then
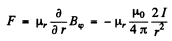
Now the maxim um value of 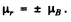 Thus the force is
Thus the force is
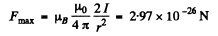
Q.155. A narrow stream of vanadium atoms in the ground state 4F3/2 is passed through a transverse strongly inhomogeneous magnetic field of length l1 = 5.0 cm as in the Stern-Gerlach experiment. The beam splitting is observed on a screen located at a distance l2 = 15 cm from the magnet. The kinetic energy of the atoms is T = 22 MeV. At what value of the gradient of the magnetic field induction B is the distance between the extreme components of the split beam on the screen equal to δ = 2.0 mm?
Ans. In the homogeneous magnetic field the atom experinces a force
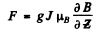
Depending on the sign of /, this can be either upward or downward. Suppose the latter is true. The atom then traverses first along a parabola inside the field and, once outside, in a straight line. The total distance between extreme lines on the screen will be
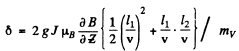
Here mv is the mass of the vanadium atom. (The first term is the displacement within the field and the second term is the displacement due to the transverse velocity acquired in the magnetic field).
Thus using 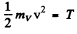
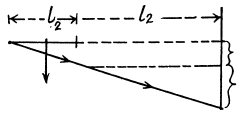
we get 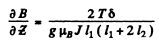
For vanadium atom in the ground state 4F3/2
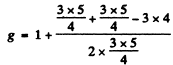
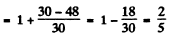
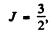 using other data, and substituting
using other data, and substituting
we get 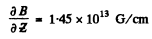
This value differs from the answer given in the book by almost a factor of 109. For neutral atoms in stem Gerlach experiments, the value T = 22MeV is much too laige. A more appropriate value will be T = 22 meV i.e. 109 times smaller. Then one gets the right answer.
Q.156. Into what number of sublevels are the following terms split in a weak magnetic field: (a) 3P0; (b) 2F5/2; (c) 4P1/2?
Ans. (a) The term 3P 0 does not split in weak magnetic field as it has zero total angular momentum.
(b) The term 2F5/2 will split into  sublevels. The shift in each sublevel is given by
sublevels. The shift in each sublevel is given by

where 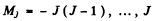 and g is the Landi factor
and g is the Landi factor
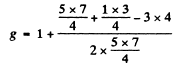
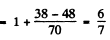
(c) In this case for the 4D1/2 term
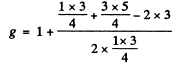
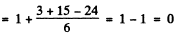
Thus the energy differences vanish and the level does not split.
Q.157. An atom is located in a magnetic field of induction B = 2.50 kG. Find the value of the total splitting of the following terms (expressed in eV units): (a) 1D; (b) 3F4.
Ans. (a) for the 1D2 term
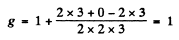
and 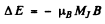
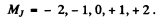 Thus the splitting is
Thus the splitting is
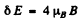
Substitution gives 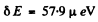
(b) For the 3F4 teim 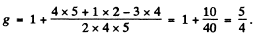
and 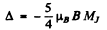
where Mj = - 4 to + 4 . Thus
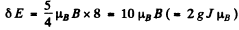
Substitution gives 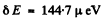
Q.158. What kind of Zeeman effect, normal or anomalous, is observed in a weak magnetic field in the case of spectral lines caused by the following transitions: (a) 1P → 1S (b) 2D5/2 → 2P3/2; (c) 3 D1 → 3P0; (d) 5l5 → 5H4?
Ans. (a) The term 1P1splits into 3 lines with Mz = ± 1, 0 in accordance with the formula
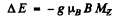
where 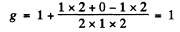
The term 1S0 does not split in weak magnetic field. Thus the transitions between 1P1 & 1S0 will result in 3 lines i.e. a normal Zeeman triplet.
(b) The term 2D5/2 will split ot in 6 terms in accordance with the formula
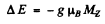
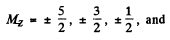
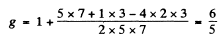
Ther term 2P3/2 will also split into 4 lines in accordance with the above formula with
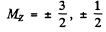 and
and 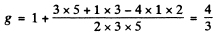
It is seen that the Z eeman splitting is auomalous as g factors are different
(c)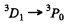
The term 3D1 splits into 3 levels (g = 5 /2)
The term 3P0 does not split. Thus the Z eeman spectrum is normal.
(d) For the 5I5 term
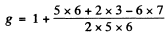
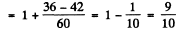
For the 5H4 term
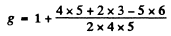
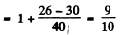
We see that the splitting in the two levels given by 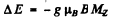 is the same though the number of levels is different (11 and 9). It is then easy to see that only the lines with following energies occur
is the same though the number of levels is different (11 and 9). It is then easy to see that only the lines with following energies occur
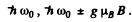
The Z eeman pattern is normal
Q.159. Determine the spectral symbol of an atomic singlet term if the total splitting of that term in a weak magnetic field of induction B = 3.0 kG amounts to ΔE = 104μeV
Ans. For a singlet term S = 0, L = J, g = 1
Then the total splitting is 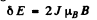
Substitution gives 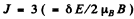
The term is 1F3.
Q.160. It is known that a spectral line λ = 612 nm of an atom is caused by a transition between singlet terms. Calculate the interval Δλ between the extreme components of that line in the magnetic field with induction B = 10.0 kG.
Ans. As the spectral line is caused by transition between singlet terms, the Z eeman effect will be normal (since g = 1 for both terms). The energy difference between extreme components of the line will be 2 μB B .This must equal
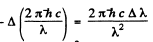
Thus 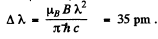
Q.161. Find the minimum magnitude of the magnetic field induction B at which a spectral instrument with resolving power λ/δλ = = 1.0.105 is capable of resolving the components of the spectral line λ = 536 nm caused by a transition between singlet terms. The observation line is at right angles to the magnetic field direction.
Ans. From the previous problem, if the components are 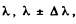 then
then
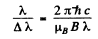
For resolution 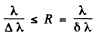 of the instrument
of the instrument
Thus
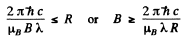
Hence the minimum megnetic induction is
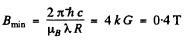
Q.162. A spectral line caused by the transition 3D1 → 3P0 experiences the Zeeman splitting in a weak magnetic field. When observed at right angles to the magnetic field direction, the interval between the neighbouring components of the split line is Δω = 1.32.1010 s -1 Find the magnetic field induction B at the point where the source is located.
Ans. The 3P0 term does not split The 3D1 term splits into 3 lines corresponding to the shift
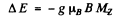
with Mz = ± 1, 0. The interval between neighbouring components is then given by

Hence
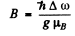
Now for the 3D1 term

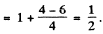
Substitution gives B = 3.00 kG. = 0.3 T.
Q.163. The wavelengths of the Na yellow doublet (2P → 2S) are equal to 589.59 and 589.00 nm. Find:
(a) the ratio of the intervals between neighbouring sublevels of the Zeeman splitting of the terms 2P3/2 and 2P1/2 in a weak magnetic field;
(b) the magnetic field induction B at which the interval between neighbouring sublevels of the Zeeman splitting of the term 2P3/2 is η = 50 times smaller than the natural splitting of the term 2P.
Ans. (a) For the 2P3/2 term
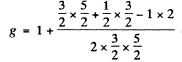
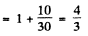
and the energy of the 2P3/2 sublevels will be
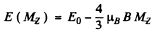
where 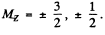 Thus, between neighbouring sublevels.
Thus, between neighbouring sublevels.
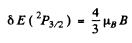
For the 2P1/2 terms
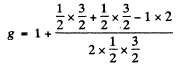

and the separation between the two sublevels into which the 2P1/2 term will split is
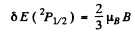
The ratio of the two splittings is 2 : 1.
(b) The interval between neighbouring Zeem an sublevels o f the 2P3/2 term is  The energy separation between D1 and D2 lines is
The energy separation between D1 and D2 lines is 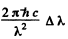 (this is the natural separation of the 2P them)
(this is the natural separation of the 2P them)
Thus 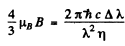
or 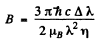
Substitution gives
B = 5-46kG
Q.164. Draw a diagram of permitted transitions between the terms 2P3/2 and 2S1/2 in a weak magnetic field. Find the displacements (in rad/s units) of Zeeman components of that line in a magnetic field B = 4.5 kG.
Ans. for the 2P3/2 level g = 4 / 3 (see above) and the eneigies of sublevels are
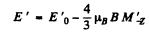
where 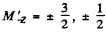 for the four sublevels
for the four sublevels
For the 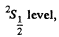 g = 2 (since L = 0) and
g = 2 (since L = 0) and
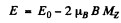
where 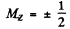
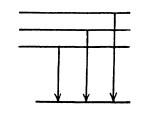
Permitted transitions must have ΔMZ = 0, ± 1
Thus only the following transitions occur
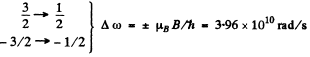
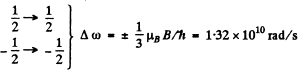
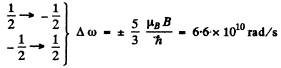
These six lines are shown below

Q.165. The same spectral line undergoing anomalous Zeeman splitting is observed in direction 1 and, after reflection from the mirror M (Fig. 6.9), in direction

2. How many Zeeman components are observed in both directions if the spectral line is caused by the transition (a) 2P3/2 → 2S1/2 ; (b) 3P2 → 3S1?
Ans.The difference arises because of different selection rules in the two cases. In (1) the line is emitted perpendicular to the field. The selection rules are then
ΔMZ = 0, ± 1
In (2) the light is emitted along die direction of die field. Then the selection rules are
ΔMZ = ± 1
ΔMZ = 0 is forbidden.
(a) In the transition 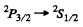
This has been considered above. In (1) we get all the six lines shown in the problem above
In (2) the line corresponding to 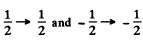 is forbidden.
is forbidden.
Then we get four lines
(b) 3P2 → 3S1
For the 3P2 level, 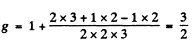
so the energies of the sublevels are
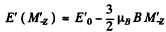
where 
For the 3S1 line, g = 2 and the energies of the sublevels are
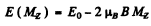
where MZ = 1, ± 0 The lines are
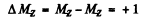

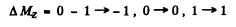
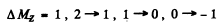
All energy differences are unequal because die two g values are unequal. There are then nine lines if viewed along (1) and Six lines if viewed along (2).
Q.166. Calculate the total splitting Ae) of the spectral line 3D3 → → 3P2 in a weak magnetic field with induction B = 3.4 kG.
Ans. For the two levels
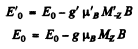
and hence the shift of the component is the value of
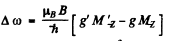
subject to the selection rule 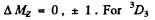
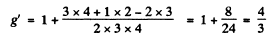
For 3P2,
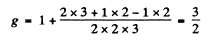
Thus 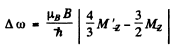
For the different transition we have the following table
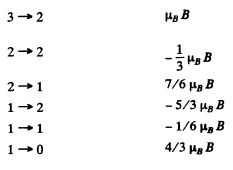
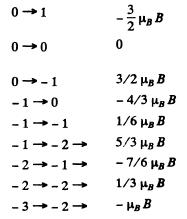
There are 15 lines in all.
The lines farthest out are 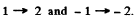
The splitting between them is the total splitting. It is
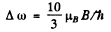
Substitution gives 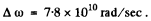

|
Explore Courses for JEE exam
|

|

















