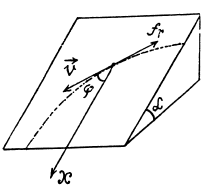
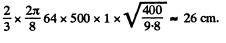Q. 106. A small disc A is placed on an inclined plane forming an angle a with the horizontal (Fig. 1.27) and is imparted an initial velocity v0. Find how the velocity of the disc depends on the angle y if the friction coefficient k = tan α and at the initial moment yo = = π/2.
Ans. The acceleration of the disc along the plane is determined by the projection of the force of gravity on this plane Fx = mg sin α and the friction force fr = kmg cos α . In our case k = tan α and therefore
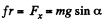
Let us find the projection of the acceleration on the derection of the tangent to the trajectory and on the x-axis :
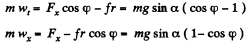
It is seen fromthis that wt = - wx, which means that the velocity v and its projection vx differ only by a constant value C which does not change with time, i.e.
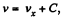
where 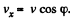 . The constant C is found from the initial condition v = v0, whence
. The constant C is found from the initial condition v = v0, whence 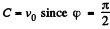 initially. Finally we obtain
initially. Finally we obtain
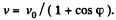
In the cource of time 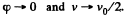 (Motion then is unaccelerated.)
(Motion then is unaccelerated.)
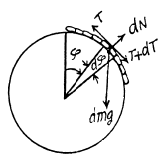
Q. 107. A chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain 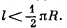
Ans. Let us consider an element of length ds at an angle qp from the vertical diameter. As the speed of this element is zero at initial instant of time, it's centripetal acceleration is zero, and hence, 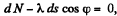 where λ is the linear mass density o f the chain Let
where λ is the linear mass density o f the chain Let 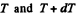 be the tension at the upper and the lower ends of ds. we have from,
be the tension at the upper and the lower ends of ds. we have from, 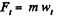

or, 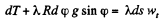
If we sum the above equation for all elements, the term 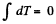 because there is no tension at the free ends, so
because there is no tension at the free ends, so
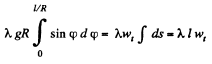
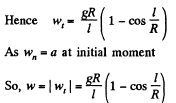
Q. 108. A small body is placed on the top of a smooth sphere of radius R. Then the sphere is imparted a constant acceleration w0 in the horizontal direction and the body begins sliding down. Find:
(a) the velocity of the body relative to the sphere at the moment of break-off;
(b) the angle θ0 between the vertical and the radius vector drawn from the centre of the sphere to the break-off point; calculate θ0 for w0 = g.
Ans. In the problem, we require the velocity of the body, realtive to the sphere, which itself moves with an acceleration w0 in horizontal direction (say towards left). Hence it is advisible to solve the problem in the frame of sphere (non-inertial frame).
At an arbitary moment, when the body is at an angle θ with the vertical, we sketch the force diagram for the body and write the second law of motion in projection form
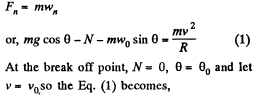
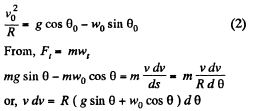

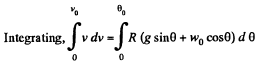
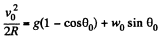 (3)
(3)
Note that the Eq. (3) can also be obtained by the work-energy theorem A = ΔT (in the frame of sphere)
therefore, 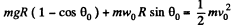
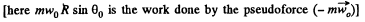
or, 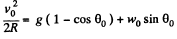
Solving Eqs. (2) and (3) we get,
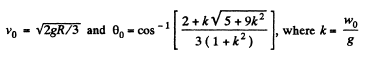
Hence 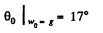
Q. 109. A particle moves in a plane under the action of a force which is always perpendicular to the particle's velocity and depends on a distance to a certain point on the plane as 1/rn, where n is a constant. At what value of n will the motion of the particle along the circle be steady?
Ans. This is not central force problem unless the path is a circle about the said point. Rather here Ft (tangential force) vanishes. Thus equation of motion becomes,
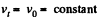
and, 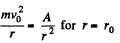
We can consider the latter equation as the equilibrium under two forces. When the motion is perturbed, we write r = r0 + x and the net force acting on the particle is,

This is opposite to the displacement 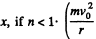 is an outward directed centrifiigul force while
is an outward directed centrifiigul force while 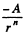 is thd inward directed external force).
is thd inward directed external force).
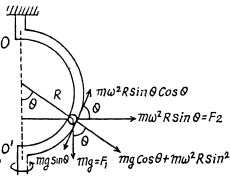
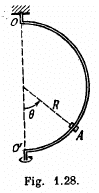
Q. 110. A sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R (Fig. 1.28). The system is set in rotation with a constant angular velocity ω about a vertical axis OO'. Find the angle θ corresponding to the steady position of the sleeve.
Ans. There are two forces on the sleeve, the weight F1 and the centrifugal force F2. We resolve both forces into tangential and normal component then the net downward tangential force on the sleeve is,
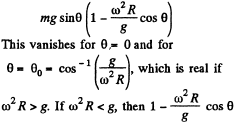
is always positive for small values of 0 and hence the net tangential force near θ = 0 opposes any displacement away from it. θ = 0 is then stable.
However  is stable because the force tends to bring the sleeve near the equilibrium position
is stable because the force tends to bring the sleeve near the equilibrium position 
If ω2R = g, the two positions coincide and becomes a stable equilibrium point.
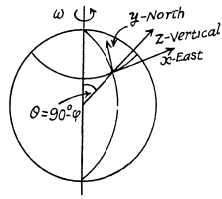
Q. 111. A rifle was aimed at the vertical line on the target located precisely in the northern direction, and then fired. Assuming the air drag to be negligible, find how much off the line, and in what direction, will the bullet hit the target. The shot was fired in the horizontal direction at the latitude φ = 60°, the bullet velocity v = 900 m/s, and the distance from the target equals s = 1.0 km.
Ans. Define the axes as shown with z along the local vertical, x due east and y due north. (We assume we are in the northern hemisphere). Then the Coriolis force has the components.
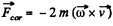
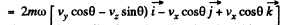
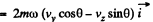
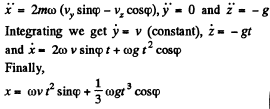
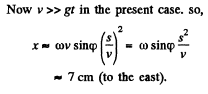
Q. 112. A horizontal disc rotates with a constant angular velocity ω = 6.0 rad/s about a vertical axis passing through its centre. A small body of mass m = 0.50 kg moves along a diameter of the disc with a velocity v' = 50 cm/s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r = 30 cm from the rotation axis.
Ans. The disc exerts three forces which are mutually perpendicular. They are the reaction of the weight, mgy vertically upward, the Coriolis force 2mv' ω perpendicular to the plane of the vertical and along the diameter, and mω2r outward along the diameter. The resultant force is,
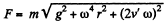
Q. 113. A horizontal smooth rod AB rotates with a constant angular velocity ω = 2.00 rad/s about a vertical axis passing through its end A. A freely sliding sleeve of mass m = 0.50 kg moves along the rod from the point A with the initial velocity v0 = 1.00 m/s. Find the Coriolis force acting on the sleeve (in the reference frame fixed to the rotating rod) at the moment when the sleeve is located at the distance r = 50 cm from the rotation axis.
Ans. The sleeve is free to slide along the rod AB. Thus only the centrifugal force acts on it.
The equation is,
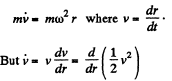
so, 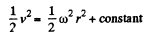
or, 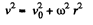
v0 being the initial velocity when r = 0. The Coriolis force is then,
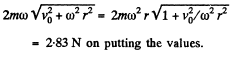
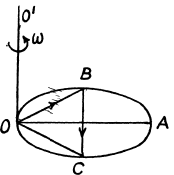
Q. 114. A horizontal disc of radius R rotates with a constant angular velocity ω about a stationary vertical axis passing through its edge. Along the circumference of the disc a particle of mass m moves with a velocity that is constant relative to the disc. At the moment when the particle is at the maximum distance from the rotation axis, the resultant of the inertial forces Fin acting on the particle in the reference frame fixed to the disc turns into zero. Find:
(a) the acceleration ω' of the particle relative to the disc;
(b) the dependence of Fin on the distance from the rotation axis.
Ans. The disc OBAC is rotating with angular velocity ω about the axis OO' passing through the edge point O. The equation of motion in rotating frame is,
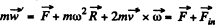
where 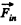 is the resultant inertial force. (pseudo force) which is the vector sum of centrifugal and Coriolis forces.
is the resultant inertial force. (pseudo force) which is the vector sum of centrifugal and Coriolis forces.
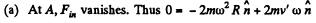
where 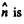 the inward drawn unit vector to the centre from the point in question, here A.
the inward drawn unit vector to the centre from the point in question, here A.
Thus, 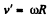
so, 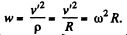
(b) At B 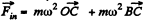
its magnitude is 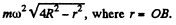
Q. 115. A small body of mass m = 0.30 kg starts sliding down from the top of a smooth sphere of radius R = 1.00 m. The sphere rotates with a constant angular velocity ω = 6.0 rad/s about a vertical axis passing through its centre. Find the centrifugal force of inertia and the Coriolis force at the moment when the body breaks off the surface of the sphere in the reference frame fixed to the sphere.
Ans. The equation of motion in the rotating coordinate system is,
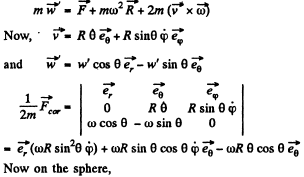
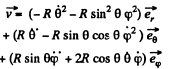
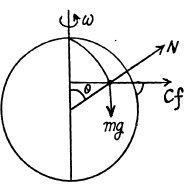
Thus the equation of motion are,
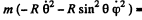
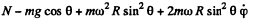
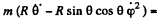
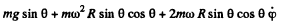
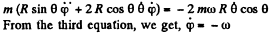
A result that is easy to understant by considering the motion in non-rotating frame. The eliminating φ we get,
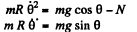
Integrating the last equation
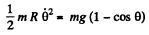
Hence
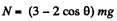
So the body must fly off for 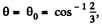 exactly as if the sphere were nonrotating.
exactly as if the sphere were nonrotating.
Now, at this point 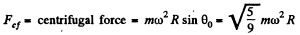
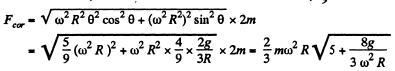
Q. 116. A train of mass m = 2000 tons moves in the latitude φ = 60° North. Find:
(a) the magnitude and direction of the lateral force that the train exerts on the rails if it moves along a meridian with a velocity v = 54 km per hour;
(b) in what direction and with what velocity the train should move for the resultant of the inertial forces acting on the train in the reference frame fixed to the Earth to be equal to zero.
Ans. (a) When the train is moving along a meridian only the Coriolis force has a lateral component and its magnitude (see the previous problem) is,
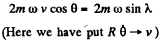
So, 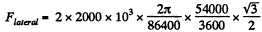
= 3.77 kN, (we write λ for the latitude)
(b) The resultant of the inertial forces acting on the train is,
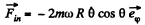
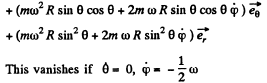
Thus 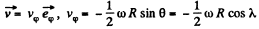
(We write λ for the latitude here)
Thus the train must move from the east to west along the 60th parallel with a speed,
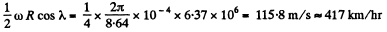
Q. 117. At the equator a stationary (relative to the Earth) body falls down from the height h = 500 m. Assuming the air drag to be negligible, find how much off the vertical, and in what direction, the body will deviate when it hits the ground.
Ans. We go to the equation given in 1.111. Here vy = 0 so we can take y = 0, thus we get for the motion in the  .
.
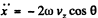
and 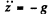
Integrating, 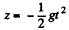
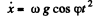
So 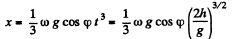
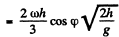
There is thus a displacement to the east of