Irodov Solutions: The Second Law of Thermodynamics Entropy- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 113. In which case will the efficiency of a Carnot cycle be higher: when the hot body temperature is increased by ΔT, or when the cold body temperature is decreased by the same magnitude?
Solution. 113. The efficiency is given by
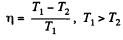
Now in the two cases the efficiencies are

Thus 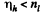
Q. 114. Hydrogen is used iu a Carnot cycle as a working substance. Find the efficiency of the cycle, if as a result of an adiabatic expansion
(a) the gas volume increases n = 2.0 times;
(b) the pressure decreases n = 2.0 times.
Solution. 114.
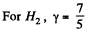
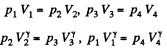
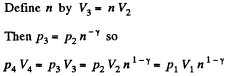
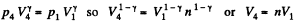
Also 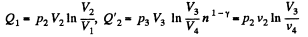
Finally 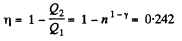
(b) 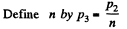
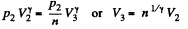
So we get the formulae here by 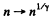 in the previous case.
in the previous case.
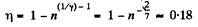
Q. 115. A heat engine employing a Carnot cycle with an efficiency of η = 10% is used as a refrigerating machine, the thermal reservoirs being the same. Find its refrigerating efficiency ε.
Solution. 115.
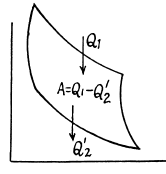
Used as a refrigerator, the refrigerating efficiency of a heat engine is given by
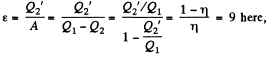
where η is the efficiency of the heat engine.
Q. 116. An ideal gas goes through a cycle consisting of alternate isothermal and adiabatic curves (Fig. 2.2). The isothermal processes proceed at the temperatures T1, T2, and T3. Find the efficiency of such a cycle, if in each isothermal expansion the gas volume increases in the same proportion.
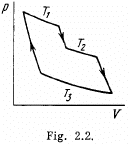
Solution. 116.
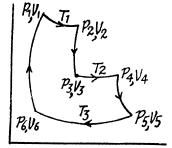
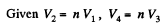
Q1 = Heat taken at the upper temperature
Now 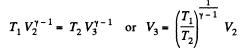
Similarly 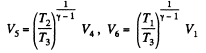
Thus Q2 = heat ejected at the lower temperature 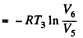
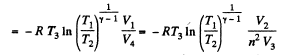

Thus 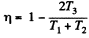
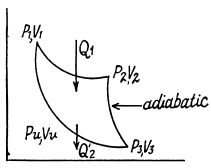
Q. 117. Find the efficiency of a cycle consisting of two isochoric and two adiabatic lines, if the volume of the ideal gas changes n = 10 times within the cycle. The working substance is nitrogen.
Solution. 117.
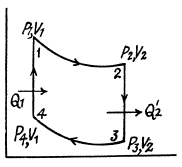
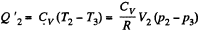
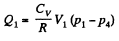


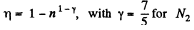
Q. 118. Find the efficiency of a cycle consisting of two isobaric and two adiabatic lines, if the pressure changes n times within the cycle. The working substance is an ideal gas whose adiabatic exponent is equal to γ.
Solution. 118.
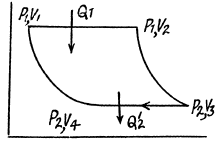
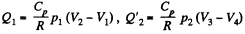
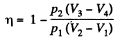
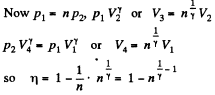
Q. 119. An ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in the isochoric heating and in the isobaric expansion.
Solution. 119. Since the absolute temperature of the gas rises n times both in the isochoric heating and in the isobaric expansion
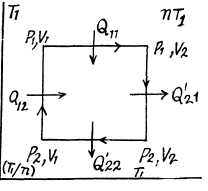
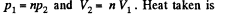
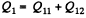
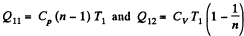
Heat rejected is Q'2 = Q'21 + Q’22 where
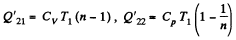
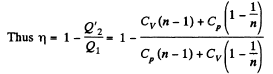
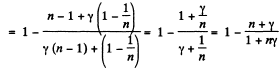
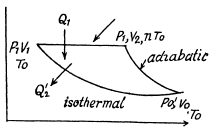
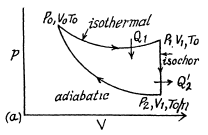
Q. 120. An ideal gas goes through a cycle consisting of
(a) isochoric, adiabatic, and isothermal lines;
(b) isobaric, adiabatic, and isothermal lines, with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the abso- lute temperature varies n-fold within the cycle.
Solution. 120.
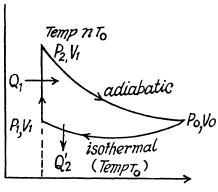
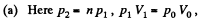
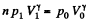
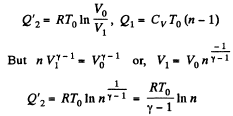
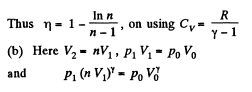
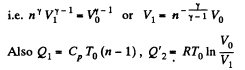
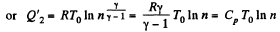
Thus 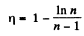
Q. 121. The conditions are the same as in the foregoing problem with the exception that the isothermal process proceeds at the maximum temperature of the whole cycle.
Solution. 121. Here the isothermal process proceeds at the maximum temperature instead of at the minimum temperature of the cycle as in Q.120.
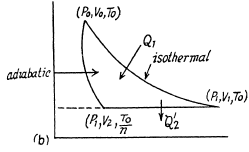
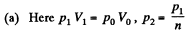

i.e. 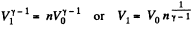
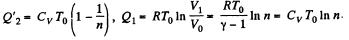
Thus 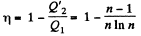
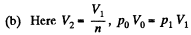
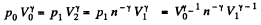
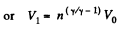
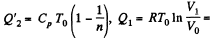
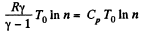
Thus 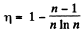
Q. 122. An ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n-fold within the cycle.
Solution. 122. The section from 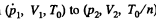 is a polytropic process of index a. We shall assume that the corresponding specific heat C is + ve.
is a polytropic process of index a. We shall assume that the corresponding specific heat C is + ve.
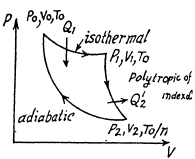
Here, 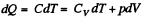
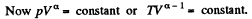

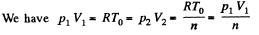
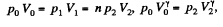
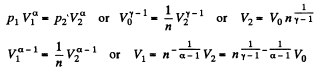

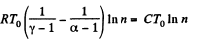
Thus 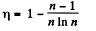
Q. 123. An ideal gas with the adiabatic exponent γ goes through a direct (clockwise) cycle consisting of adiabatic, isobaric, and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas (a) increases n-fold; (b) decreases n-fold.
Solution. 123.
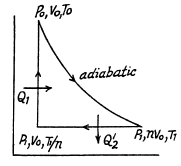
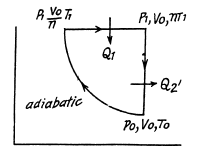
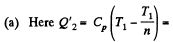
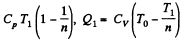
Along the adiabatic line 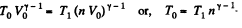
so 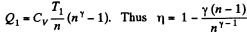
(b) 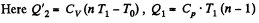
Along the adiabatic line 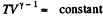
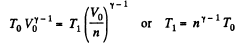
Thus 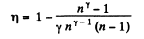
Q. 124. Calculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric lines, if in the isothermal process the volume of the ideal gas with the adiabatic exponent γ
(a) increases n-fold;
(b) decreases n-fold.
Solution. 124.
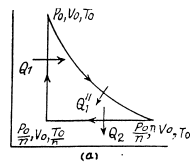
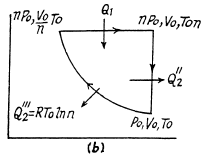
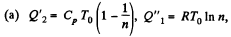
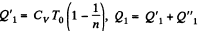
So 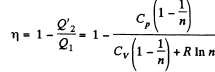
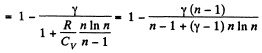
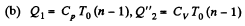
So 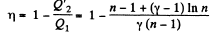
Q. 125. Find the efficiency of a cycle consisting of two isochoric and two isothermal lines if the volume varies v-fold and the absolute temperature τ-fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
Solution. 125.
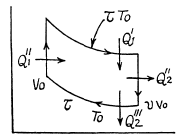
We have
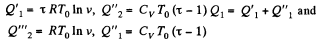
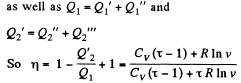
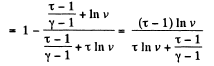
Q. 126. Find the efficiency of a cycle consisting of two isobaric and two isothermal lines if the pressure varies n-fold and the absolute temperature τ-fold within the cycle. The working substance is an ideal gas with the adiabatic exponent γ.
Solution. 126.
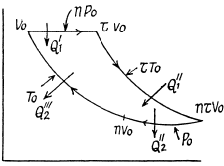
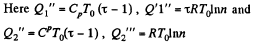
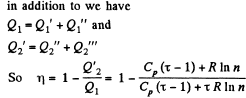
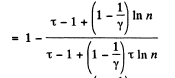
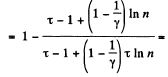
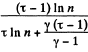
Q. 127. An ideal gas with the adiabatic exponent γ goes through a cycle (Fig. 2.3) within which the absolute temperature varies τ-fold. Find the efficiency of this cycle.
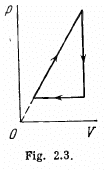
Solution. 127.
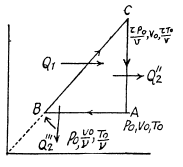
Because of the linearity of the section
BC whose equation is
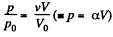

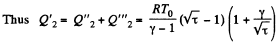
Along BC, the specific heat C is given by
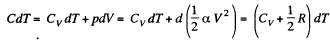
Thus 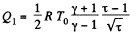
Finally 
Q. 128. Making use of the Clausius inequality, demonstrate that all cycles having the same maximum temperature Tmax and the same minimum temperature Tmin are less efficient compared to the Carnot cycle with the same Tmax and Tmin•
Solution. 128. We write Claussius inequality in the form
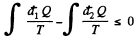
where 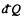 is the heat transeferred to the system but
is the heat transeferred to the system but  is heat rejected by the system, both are +ve and this explains the minus sign before
is heat rejected by the system, both are +ve and this explains the minus sign before 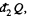
In this inequality  and we can write
and we can write
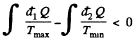
Thus 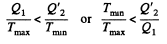
or 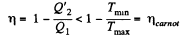
Q. 129. Making use of the Carnot theorem, show that in the case of a physically uniform substance whose state is defined by the parameters T and V
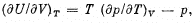
where U (T, V) is the internal energy of the substance.
Instruction. Consider the infinitesimal Carnot cycle in the variables p, V.
Solution. 129. We consider an infinitesimal carnot cycle with isothermal process at temperatures T + dT and T.
Let δA be the work done in the cycle and δQ, be the heat received at the higher temperature. Then by Carnot's theorem
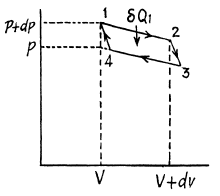
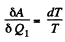
On the other hand 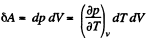
while 
Hence 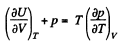
Q. 130. Find the entropy increment of one mole of carbon dioxide when its absolute temperature increases n = 2.0 times if the process of heating is (a) isochoric; (b) isobaric. The gas is to be regarded as ideal.
Solution. 130. (a) In an isochoric process the entropy change will be
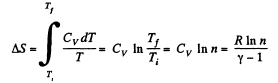
For carbon dioxide 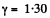
so, 
(b) For an isobaric process,
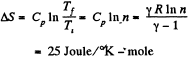
Q. 131. The entropy of v = 4.0 moles of an ideal gas increases by ΔS = 23 J/K due to the isothermal expansion. How many times should the volume v = 4.0 moles of the gas be increased?
Solution. 131. In an isothermal expansion

Q. 132. Two moles of an ideal gas are cooled isochorically and then expanded isobarically to lower the gas temperature back to the initial value. Find the entropy increment of the gas if in this process the gas pressure changed n = 3.3 times.
Solution. 132.
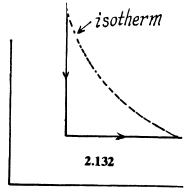
The entropy change depends on the final & initial states only, so we can calculate it directly along the isotherm, it is 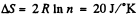
(assuming that the final volume is n times the inital volume)
Q. 133. Helium of mass m =1.7 g is expanded adiabatically n = 3.0 times and then compressed isobarically down to the initial volume. Find the entropy increment of the gas in this process.
Solution. 133. If the initial temperature is T0 and volume is V0 then in adiabatic expansion,
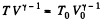
so, 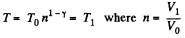
V1 being the volume at the end of the adiabatic process. There is no entropy change in this process. Next the gas is compressed isobarically and the net entropy change is

But 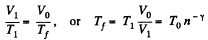
So 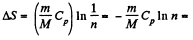
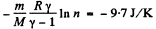
FAQs on Irodov Solutions: The Second Law of Thermodynamics Entropy- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the second law of thermodynamics? |  |
| 2. How is entropy related to the second law of thermodynamics? |  |
| 3. Can entropy of a system decrease in certain cases? |  |
| 4. What are some practical applications of the second law of thermodynamics? |  |
| 5. How does the second law of thermodynamics relate to the concept of heat flow? |  |

|
Explore Courses for JEE exam
|

|

















