Irodov Solutions: Thermal Radiation. Quantum Nature of Light- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.261. From the standpoint of the corpuscular theory demonstrate that the momentum transferred by a beam of parallel light rays per unit time does not depend on its spectral composition but depends only on the energy flux 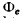
Ans. The statement made in the question is not always correct. However it is correct in certain cases, for example, when light is incident on a perfect reflector or perfect absorber.
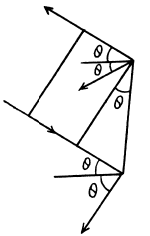
Consider the former case. If light is incident at an angle θ and reflected at the angle θ, then momentum transfered by each photon is
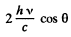
If there are n(v) dv photons in frequency interval (v, v + dv), then total momentum transfered is
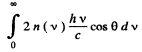
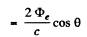

Q.262. A laser emits a light pulse of duration ζ = 0.13 ms and energy E = 10 J. Find the mean pressure exerted by such a light pulse when it is focussed into a spot of diameter d = 10 pm on a surface perpendicular to the beam and possessing a reflection coefficient ρ = 0.50.
Ans. The mean pressure <p> is related to the force Fexerted by the beam by
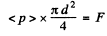
The force F equals momentum transfered per second. This is (assuming that photons, not reflected, are absorbed)
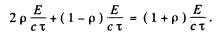
The first term is the momentum transfered on reflection (see problem (261)); the second on absorption.
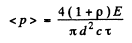
Substituting the values we get
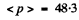 atmosphere.
atmosphere.
Q.263. A short light pulse of energy E = 7.5 J falls in the form of a narrow and almost parallel beam on a mirror plate whose reflection coefficient is ρ = 0.60. The angle of incidence is 30°. In terms of the corpuscular theory find the momentum transferred to the plate.
Ans. The momentum transfered to the plate is

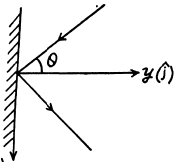
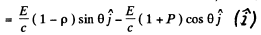
Its magnitude is
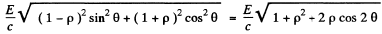
Substitution gives 35 n N.s as the answer.
Q.264. A plane light wave of intensity I = 0.20 W/cm2 falls on a plane mirror surface with reflection coefficient ρ = 0.8. The angle of incidence is 45°. In terms of the corpuscular theory find the magnitude of the normal pressure exerted by light on that surface.
Ans. Suppose the mirror has a surtace area A.
The incident bean then has a cross section of A cos θ and the incident energy is 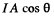 ; Then the momentum transfered per second ( = Force ) is from the last problem
; Then the momentum transfered per second ( = Force ) is from the last problem
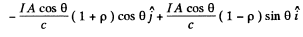
The normal pressure is then 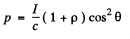
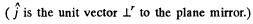
Putting in the values
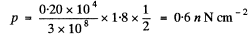
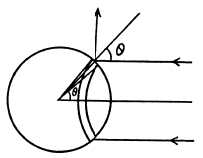
Q.265. A plane light wave of intensity I = 0.70 W/cm2 illuminates a sphere with ideal mirror surface. The radius of the sphere is R = 5.0 cm. From the standpoint of the corpuscular theory find the force that light exerts on the sphere.
Ans. We consider a strip defined by the angular range 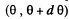 From the previous problem the normal pressure exerted on this strip is
From the previous problem the normal pressure exerted on this strip is
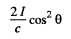
This pressure gives rise to a force whose resultant, by symmetry is in the direction of the incident light. Thus
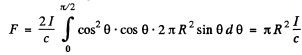
Putting in the values
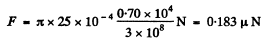
Q.266. An isotropic point source of radiation power P is located on the axis of an ideal mirror plate. The distance between the source and the plate exceeds the radius of the plate n-fold. In terms of the corpuscular theory find the force that light exerts on the plate.
Ans. Consider a ring of radius x on the plate. The normal pressure on this ring is, by problem (264),
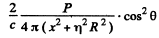
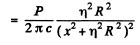
The total force is then
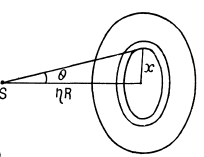
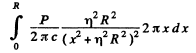
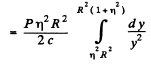
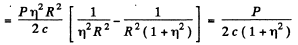
Q.267. In a reference frame K a photon of frequency ω falls normally on a mirror approaching it with relativistic velocity V. Find the momentum imparted to the mirror during the reflection of the photon (a) in the reference frame fixed to the mirror; (b) in the frame K.
Ans. (a) In the reference frame fixed to the mirror, the frequency of the photon is, by the Doppler shift formula
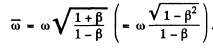
(see Eqn. (5.6b))
In this frame momentum imparted to the mirr of is
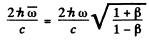
(b) In the K frame, the incident particle carries a momentum of 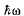 / c and returns with momentum
/ c and returns with momentum
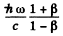
(see problem 229). The momentum imparted to the mirror, then, has the magnitude
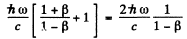
Here 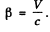
Q.268. A small ideal mirror of mass m = 10 mg is suspended by a weightless thread of length l = 10 cm. Find the angle through which the thread will be deflected when a short laser pulse with energy E = 13 J is shot in the horizontal direction at right angles to the mirror. Where does the mirror get its kinetic energy?
Ans. When light falls on a small mirror and is reflected by it, the mirror recoils. The energy of recoil is obtained from the incident beam photon and the frequency of reflected photons is less than the frequency of the incident photons. This shift of frequency can however be neglected in calculating quantities related to recoil (to a first approximation.) Thus, the momentum acquired by the mirror as a result of the laser pulse is
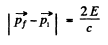
Or assuming 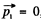 , we get
, we get
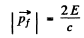
Hence the kinetic energy of the mirror is
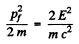
Suppose the mirror is deflected by an angle θ. Then by conservation of energy final P.E.
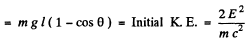
or 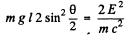
or 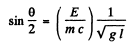
Using the data. 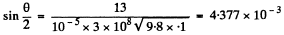
This gives θ = 0.502 degrees .
Q.269. A photon of frequency ωo is emitted from the surface of a star whose mass is M and radius R. Find the gravitational shift of frequency Δω/ωo of the photon at a very great distance from the star.
Ans. We shall only consider stars which are not too compact so that the gravitational field at their surface is weak :
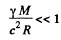
We shall also clarify the problem by making clear the meaning of the (slightly changed) notation.
Suppose the photon is emitted by some atom whose total relativistic energies (including the rest mass) are E1 & E2 with E1 < E2. These energies are defined in the absence of gravitational field and we have
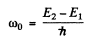
as the frequency at infinity o f the photon that is emitted in 2 → 1 transition. On the surface of the star, the energies have the values
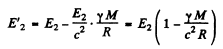
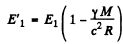
Thus, from 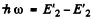 we get
we get
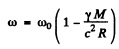
Here ω is the frequency of the photon emitted in the transition 2 → 1 when the atom is on the surface of the star. In shows that the frequency of spectral lines emitted by atoms on the surface of some star is less than the frequency of lines emitted by atoms here on earth (where the gravitational effect is quite small).
Finally 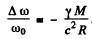
The answer given in /the book is incorrect in general though it agrees with the above result for 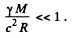
Q.270. A voltage applied to an X-ray tube being increased η = = 1.5 times, the short-wave limit of an X-ray continuous spectrum shifts by Δλ = 26 pm. Find the initial voltage applied to the tube.
Ans. The general formula is
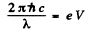
Thus 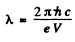
Now 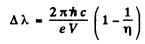
Hence 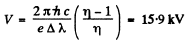
Q.271. A narrow X-ray beam falls on a NaC1 single crystal. The least angle of incidence at which the mirror reflection from the system of crystallographic planes is still observed is equal to α = = 4.1°. The interplanar distance is d = 0.28 nm. How high is the voltage applied to the X-ray tube?
Ans. We have as in the above problem
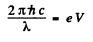
On the other hand, from Bragg’s law 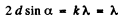
since k = 1 when α takes its smallest value.
Thus 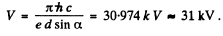
Q.272. Find the wavelength of the short-wave limit of an X-ray continuous spectrum if electrons approach the anticathode of the tube with velocity v = 0.85 c, where c is the velocity of light.
Ans. The wavelength of X - rays is the least w hen all the K .E. of the electrons approaching the anticathode is converted into the eneigy of X - rays.
But the K.E. of electron is

( me2 = rest mass eneigy of electrons = 0.511 MeV )
Thus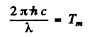
or 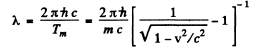
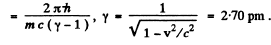
Q.273. Find the photoelectric threshold for zinc and the maximum velocity of photoelectrons liberated from its surface by electromagnetic radiation with wavelength 250 nm.
Ans. The work function of zinc is

The threshold wavelength for photoelectric effect is given by

or

The maximum velocity of photoelectrons liberated by light of wavelength λ is given by
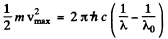
So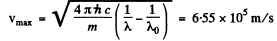
Q.274. Illuminating the surface of a certain metal alternately with light of wavelengths λ1 = 0.35 tim and λ2 = 0.54 lam, it was found that the corresponding maximum velocities of photoelectrons differ by a factor η = 2.0. Find the work function of that metal.
Ans. From the last equation of the previous problem, we find
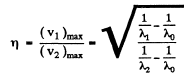
Thus 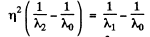
or 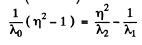
and 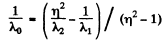
So 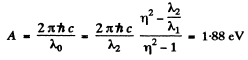
Q.275. Up to what maximum potential will a copper ball, remote from all other bodies, be charged when irradiated by electromagnetic radiation of wavelength λ = 140 nm?
Ans. When light of sufficiently short wavelength falls on the ball, photoelectrons are ejected and the copper ball gains positive change. The charged ball tends to resist further emission of electrons by attracting them. When the copper ball has enough chaige even the most energetic electrons are unable to leave it We can calculate this final maximum potential of the copper ball. It is obviously equal in magnitude (in volt) to the maximum K.E of electrons (in electron volts) initially emitted. Hence
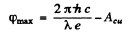
= 8.86 - 4.47 = 4.39 volts
(Acu is the work function of copper.)
FAQs on Irodov Solutions: Thermal Radiation. Quantum Nature of Light- 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is thermal radiation and how does it relate to the quantum nature of light? |  |
| 2. What is the significance of the quantum nature of light in understanding thermal radiation? |  |
| 3. How does the quantum nature of light challenge classical theories of thermal radiation? |  |
| 4. How does the quantum nature of light affect the intensity and wavelength distribution of thermal radiation? |  |
| 5. How can the quantum nature of light be experimentally verified in the context of thermal radiation? |  |

|
Explore Courses for JEE exam
|

|

















