Irodov Solutions: Thermal Radiation. Quantum Nature of Light- 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.276. Find the maximum kinetic energy of photoelectrons liberated from the surface of lithium by electromagnetic radiation whose electric component varies with time as E = a (1 + cos ωt) cos ω0t, where a is a constant, ω = 6.0.1014 s-1 and ωo = 3.60.1015 s-1 .
Ans. We write
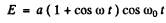
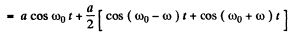
It is obvious that light has three frequencies and the maximum K.E. of photo electrons ejected is
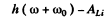
where 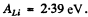 . Substituting we get 0.37 eV.
. Substituting we get 0.37 eV.
Q.277. Electromagnetic radiation of wavelength λ = 0.30 μm falls on a photocell operating in the saturation mode. The corresponding spectral sensitivity of the photocell is J = 4.8 mA/W. Find the yield of photoelectrons, i.e. the number of photoelectrons produced by each incident photon.
Ans. Suppose N photons fall on the photocell per sec. Then the power incident is
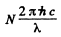
This will give rise to a photocurrent of 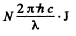
which means that 
electrons have been emitted. Thus the number of photoelectrons produced by each photon is
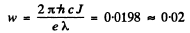
Q.278. There is a vacuum photocell whose one electrode is made of cesium and the other of copper. Find the maximum velocity of photoelectrons approaching the copper electrode when the cesium electrode is subjected to electromagnetic radiation of wavelength 0.22 p.m and the electrodes are shorted outside the cell.
Ans. A simple application of Einstein’s equation
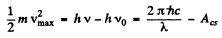
gives incorrect result in this case because the photoelectrons emitted by the Cesium electrode are retarded by the small electric Geld that exists between the cesium electrode and the Copper electrode even in the absence of external emf. This small electric Geld is caused by the contact potential difference whose magnitude equals the difference of work functions
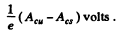
Its physical origin is explained below.
The maximum velocity of the photoelectrons reaching the copper electrode is then
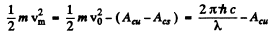
Here v0 is the maximum velocity of the photoelectrons immediately after emission. Putting the values we get, on using 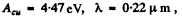
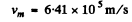
The origin of contact potential difference is the following. Inside the metals free electrons can be thought of as a Fermi gas which occupy energy levels upto a maximum called the Fermi energy EP . The work function A measures the depth of the Fermi level.
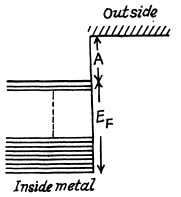
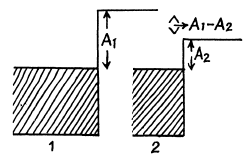
When two metals 1 & 2 are in contact, electrons flow from one to the other till their Fermi levels are the same. This requires the appearance of contact potential difference of A1 - A2 between the two metals externally.
Q.279. A photoelectric current emerging in the circuit of a vacuum photocell when its zinc electrode is subjected to electromagnetic radiation of wavelength 262 nm is cancelled if an external decelerating voltage 1.5 V is applied. Find the magnitude and polarity of the outer contact potential difference of the given photocell.
Ans. The maximum K.E. of the photoelectrons emitted by the Zn cathode is
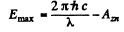
On calculating this comes out to be 0.993 eV ≈ 1.0 eV Since an external decelerating voltage of 1.5 V is required to cancel this current, we infer that a contact potential difference of 1.5 - 1.0 = 0.5 V exists in the circuit whose polarity is opposite of the decelerating voltage.
Q.280. Compose the expression for a quantity whose dimension is length, using velocity of light c, mass of a particle m, and Planck's constant 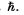 What is that quantity?
What is that quantity?
Ans. The unit of 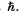 is Joule-sec. Since mc2 is the rest mass energy,
is Joule-sec. Since mc2 is the rest mass energy, 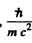 as dimension of time and multiplying by c we get a quantity
as dimension of time and multiplying by c we get a quantity
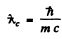
whose dimension is length. This quantity is called reduced compton wavelength.
(The name compton wavelength is traditionally reserved for m 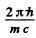 )
)
Q.281. Using the conservation laws, demonstrate that a free electron cannot absorb a photon completely.
Ans. We consider the collision in the rest frame of the initial electron. Then the reaction is
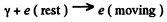
Energy momentum conservation gives
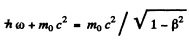
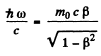
where ω is the angular frequency of the photon.
Eliminating hω we get
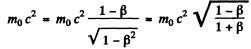
This gives β = 0 which implies 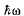 = 0
= 0
But a zero energy photon means no photon.
282. Explain the following features of Compton scattering of light by matter:
(a) the increase in wavelength Δλ, is independent of the nature of the scattering substance;
(b) the intensity of the displaced component of scattered light grows with the increasing angle of scattering and with the diminishing atomic number of the substance;
(c) the presence of a non-displaced component in the scattered radiation.
Ans. (a) Compton scattering is the scattering of light by free electrons. (The free electrons are the electrons whose binding is much smaller than the typical energy transfer to the electrons). For this reason the increase in wavelength Δλ is independent of the nature of the scattered substance.
(b) This is because the effective number of free electrons increases in both cases. With increasing angle of scattering, the energy transfered to electrons increases. With diminishing atomic number of the substance the binding energy of the electrons decreases.
(c) The presence of a non-displaced component in the scattered radiation is due to scattering from strongy bound (inner) electrons as well as nuclei. For scattering by these the atom essentially recoils as a whole and there is very little energy transfer.
Q.283. A narrow monochromatic X-ray beam falls on a scattering substance. The wavelengths of radiation scattered at angles θ1 = 60° and θ2 = 120° differ by a factor η = 2.0. Assuming the free electrons to be responsible for the scattering, find the incident radiation wavelength.
Ans. Let λ0 - wavelength of the incident radiation.
Then wavelength of the radiation scattened at θ1 = 60°
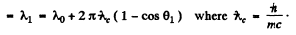
and similarly
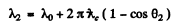
From the data 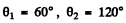
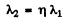
Thus 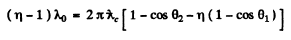
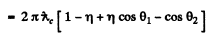
Hence 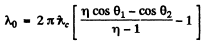
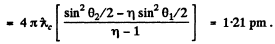
The expression λ0 given in the book contains misprints.
Q.284. A photon with energy 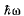 = 1.00 MeV is scattered by a stationary free electron. Find the kinetic energy of a Compton electron if the photon's wavelength changed by η = 25% due to scattering.
= 1.00 MeV is scattered by a stationary free electron. Find the kinetic energy of a Compton electron if the photon's wavelength changed by η = 25% due to scattering.
Ans. The wave lengths of the photon has increased by a fraction η so its final wavelength is
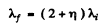
and its energy is 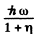
The K.E. of the compton electron is the energy lost by the photon and is
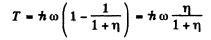
Q.285. A photon of wavelength λ = 6.0 pm is scattered at right angles by a stationary free electron. Find:
(a) the frequency of the scattered photon;
(b) the kinetic energy of the Compton electron.
Ans. (a) From the Compton formula
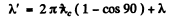
Thus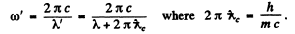
Substituting the values, we get 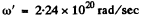
(b) The kinetic energy of the scattered electron (in the frame in which the initial electron was stationary) is simply
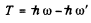
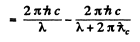
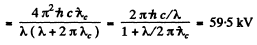
Q.286. A photon with energy how 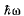 = 250 keV is scattered at an angle θ = 120° by a stationary free electron. Find the energy of the scattered photon.
= 250 keV is scattered at an angle θ = 120° by a stationary free electron. Find the energy of the scattered photon.
Ans. The wave length of the incident photon is
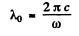
Then the wavelength of the final photon is
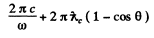
and the energy of the final photon is
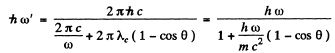
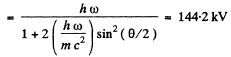
Q.287. A photon with momentum p = 1.02 MeV/c, where c is the velocity of light, is scattered by a stationary free electron, changing in the process its momentum to the value p' = 0.255 MeV/c. At what angle is the photon scattered?
Ans. We use the equation
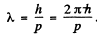
Then from Compton formula
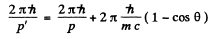
so 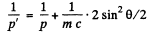
Hence 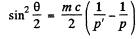
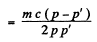
or 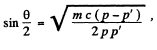
Substituting from the data
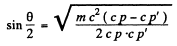
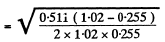
This gives θ = 120.2 degrees.
Q.288. A photon is scattered at an angle θ = 120° by a stationary free electron. As a result, the electron acquires a kinetic energy T = 0.45 MeV. Find the energy that the photon had prior to scattering.
Ans. From the Compton formula
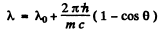
From conservation of eneigy
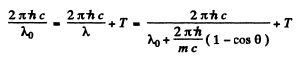
or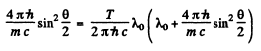
or introducing 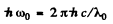
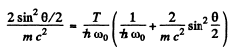
Hence 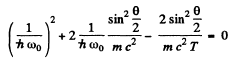
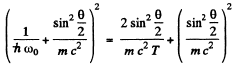

or 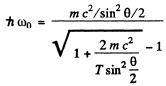
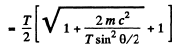
Substituting we get 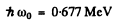
Q.289. Find the wavelength of X-ray radiation if the maximum kinetic energy of Compton electrons is Tmax = 0.19 MeV.
Ans. We see from the previous problem that the electron gains the maximum K.E. when the photon is scattered backwards θ = 180°. Then
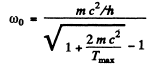
Hence
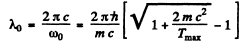
Substituting the values we get Δλ = 3.695 pm .
Q.290. A photon with energy 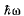 = 0.15 MeV is scattered by a stationary free electron changing its wavelength by Δλ = 3.0 pm. Find the angle at which the Compton electron moves.
= 0.15 MeV is scattered by a stationary free electron changing its wavelength by Δλ = 3.0 pm. Find the angle at which the Compton electron moves.
Ans. Refer to the diagram. Energy momentum conservation gives
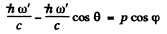
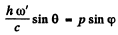
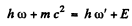
Where 
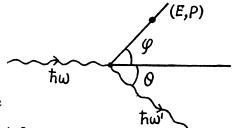
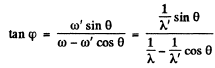
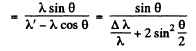
where 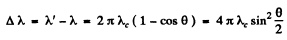
Hence 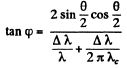
But 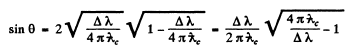
Thus 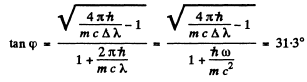
Q.291. A photon with energy exceeding η = 2.0 times the rest energy of an electron experienced a head-on collision with a stationary free electron. Find the curvature radius of the trajectory of the Compton electron in a magnetic field B = 0.12 T. The Compton electron is assumed to move at right angles to the direction of the field.
Ans. By head on collision we understand that the electron moves on in the direction of the incident photon after the collision and the photon is scaltered backwards. Then, let us write
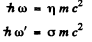
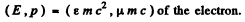
Then by energy momentum conservation (cancelling factors of mc2 and me )
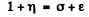
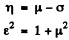
So eliminating σ & ε 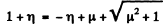
or 
Squaring 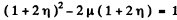
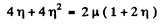
or 
Thus the momentum of the Compton electron is

Now in a m agnetic field p = B e p
Thus 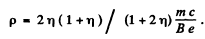
Substituting the values ρ = 3.412 cm .
Q.292. Having collided with a relativistic electron, a photon is deflected through an angle θ = 60° while the electron stops. Find the Compton displacement of the wavelength of the scattered photon.
Ans. This is the inverse of usual compton scattering.
When we write down the energy-momentum conservation equation for this process we find that they are the same for the inverse process as they arc for the usual process.
If follows that the formula for compton shift is applicable \ except that the energy (frequency) of the photon is ^ increased on scattering and the wavelength is shifted downward. With this understanding, we write
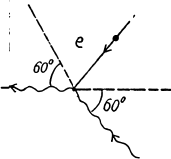
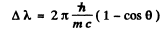
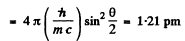

|
Explore Courses for JEE exam
|

|

















