Irodov Solutions: Thermal Radiation. Quantum Nature of Light- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.246. Using Wien's formula, demonstrate that
(a) the most probable radiation frequency 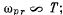
(b) the maximum spectral density of thermal radiation
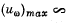
(c) the radiosity 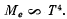
Ans. a ) The most probable radiation frequency 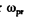 is the frequency for which
is the frequency for which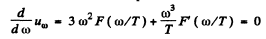
The maximum frequency is the root other than ω = 0 of this equation. It is

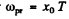 where x0 is the solution of the transcendental equation
where x0 is the solution of the transcendental equation
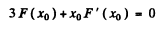
(b) The maximum spectral density is the density corresponding to most probable frequency. It is
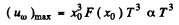
where x0 is defined above,
(c) The radiosity is
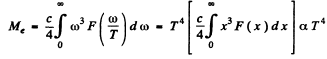
Q.247. The temperature of one of the two heated black bodies is T1 = 2500 K. Find the temperature of the other body if the wavelength corresponding to its maximum emissive capacity exceeds by Δλ = 0.50 gm the wavelength corresponding to the maximum emissive capacity of the first black body.
Ans. For the first black body
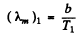
Then
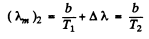
Hence
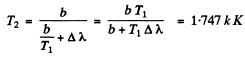
Q.248. The radiosity of a black body is Me =3.0 W/cm2. Find the wavelength corresponding to the maximum emissive capacity of that body.
Ans. From the radiosity we get the temperature of the black body. It is
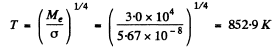
Hence the wavelength corresponding to the maximum emissive capacity of the body is
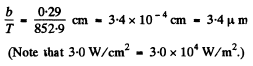
Q.249. The spectral composition of solar radiation is much the same as that of a black body whose maximum emission corresponds to the wavelength 0.48μm. Find the mass lost by the Sun every second due to radiation. Evaluate the time interval during which the mass of the Sun diminishes by 1 per cent.
Ans. The black body temperature of the sun maybe taken as
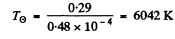
Thus the radiosity is
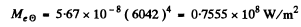
Energy lost by sun is
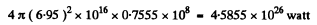
This corresponds to a mass loss of
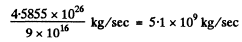
The sun loses 1 % of its mass in
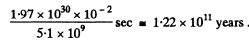
Q.250. Find the temperature of totally ionized hydrogen plasma of density p = 0.10 g/cm3 at which the thermal radiation pressure is equal to the gas kinetic pressure of the particles of plasma. Take into account that the thermal radiation pressure p = u/3, where u is the space density of radiation energy, and at high temperatures all substances obey the equation of state of an ideal gas.
Ans. For an ideal gas p = n k T where n = number density of the particles and 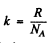 i.s Boltzman constant In a fully ionized hydrogen plasma, both H ions (protons) and electrons contribute to pressure but since the mass of electrons is quite small
i.s Boltzman constant In a fully ionized hydrogen plasma, both H ions (protons) and electrons contribute to pressure but since the mass of electrons is quite small 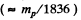 only protons contribute to mass density. Thus
only protons contribute to mass density. Thus
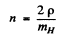
and 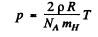
Where 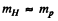 is the proton or hydrogen mass.
is the proton or hydrogen mass.
Equating this to thermal radiation pressure
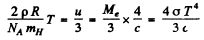
Then 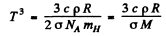
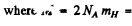 molecular weight of hydrogen = 2 x10-3 kg .
molecular weight of hydrogen = 2 x10-3 kg .
Thus 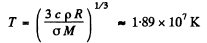
Q.251. A copper ball of diameter d = 1.2 cm was placed in an evacuated vessel whose walls are kept at the absolute zero temperature. The initial temperature of the ball is To = 300 K. Assuming the surface of the ball to be absolutely black, find how soon its temperature decreases η = 2.0 times.
Ans. In time dt after the instant t when the temperature of the ball is T, it loses
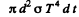
Joules of energy. As & result its temperature falls by - dT and
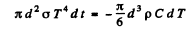
Where ρ = density of copper, C = its sp.heat
Thus 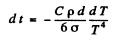
or 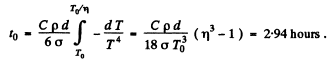
Q.252. There are two cavities (Fig. 5.39) with small holes of equal diameters d = 1.0 cm and perfectly reflecting outer surfaces. The
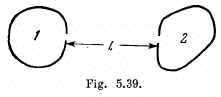
distance between the holes is l = 10 cm. A constant temperature T1 = 1700 K is maintained in cavity 1. Calculate the steady-state temperature inside cavity 2. Instruction. Take into account that a black body radiation obeys the cosine emission law.
Ans. Taking account of cosine low of emission we write for the energy radiated per second by the hole in cavity # 1 as
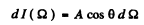
where A is an constant, dΩ is an element of solid angle around some direciton defined by the symbol Ω . Integrating over the whole forward hemisphere we get
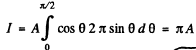

We find A by equating this to the quantity 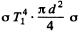 is stefan- Boltzman constant and d is the diameter of th hole.
is stefan- Boltzman constant and d is the diameter of th hole.
Then 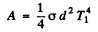
Now energy reaching 2 from 1 is 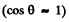
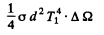
where 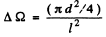 is the solid angle subtended by the hole of 2 at 1. {We are assuming
is the solid angle subtended by the hole of 2 at 1. {We are assuming
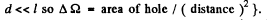
This must equal 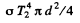
which is the energy emitted by 2. Thus equating
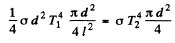
or 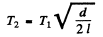
Substituting we get T2 = 0.380 k K = 380 K .
Q.253. A cavity of volume V = 1.0 1 is filled with thermal radiation at a temperature T = 1000 K. Find:
(a) the heat capacity Cv;
(b) the entropy S of that radiation.
Ans. (a ) The total internal eneigy of the cavity is
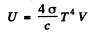
Hence 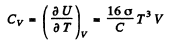
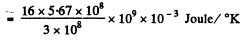
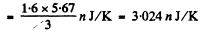
(b) From first law
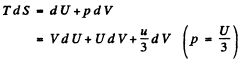
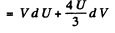
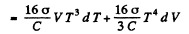
so 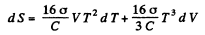

Hence 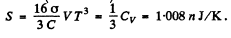
Q.254. Assuming the spectral distribution of thermal radiation energy to obey Wien's formula 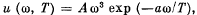 where a = 7.64 ps•K , find for a temperature T = 2000 K the most probable
where a = 7.64 ps•K , find for a temperature T = 2000 K the most probable
(a) radiation frequency;
(b) radiation wavelength.
Ans. We are given
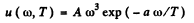
(a) then 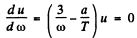
so 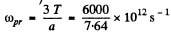
(b) We determine the spectral distribution in wavelength.
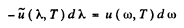
But 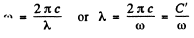
so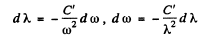
(we have put a minus sign before dλ to subsume just this fact dλ is -ve where dω is +ve.)
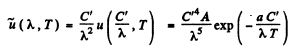
This is maximum when
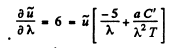
or 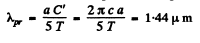
Q.255. Using Planck's formula, derive the approximate expressions for the space spectral density uω of radiation
(a) in the range where hω << kT (Rayleigh-Jeans formula);
(b) in the range where Nω >> kT (Wien's formula).
Ans. From Planek’s formula
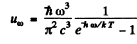
(a) In a range 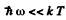 (long wavelength or high temperature).
(long wavelength or high temperature).
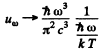
 for small x.
for small x.
(b) In the range  (high frequency or low temperature) :
(high frequency or low temperature) :
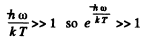
and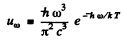
Q.256. Transform Planck's formula for space spectral density uω. of radiation from the variable ω to the variables v (linear frequency) and λ (wavelength).
Ans. We write
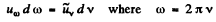
Then
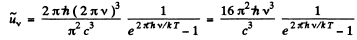
Also 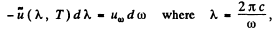
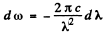
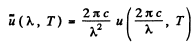
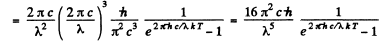
Q.257. Using Planck's formula, find the power radiated by a unit area of a black body within a narrow wavelength interval Δλ = = 1.0 nm close to the maximum of spectral radiation density at a temperature T = 3000 K of the body.
Ans. We write the required power in terms of the radiosity by considering only the energy radiated in the given range. Then from the previous problem
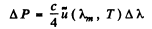
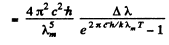
But 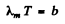
so 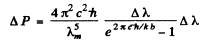
Using the data
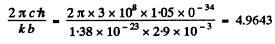
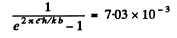
and 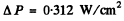
Q.258. Fig. 5.40 shows the plot of the function y (x) representing a fraction of the total power of thermal radiation falling within
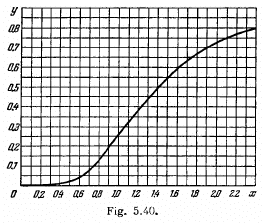
the spectral interval from 0 to x. Here 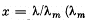 is the wavelength corresponding to the maximum of spectral radiation density). Using this plot, find:
is the wavelength corresponding to the maximum of spectral radiation density). Using this plot, find:
(a) the wavelength which divides the radiation spectrum into two equal (in terms of energy) parts at the temperature 3700 K;
(b) the fraction of the total radiation power falling within the visible range of the spectrum (0.40-0.76 Rm) at the temperature 5000 K;
(c) how many times the power radiated at wavelengths exceeding 0.76 Jim will increase if the temperature rises from 3000 to 5000 K.
Ans. (a) From the curve of the function y(x) we see that y = 0-5 when x = 1.41
Thus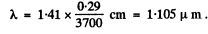
(b) At 5000 K
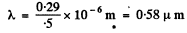
So the visible range (0.40 to 0.70) ^im corresponds to a range (0.69 to 1.31) of x
From the curve
y (0.69 ) = 0.07
y( 1-31) = 0.44
so the fraction is 0.37
(c) The value of x corresponding to 0.76 are
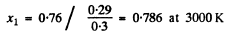
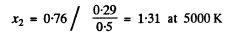
The requisite fraction is then

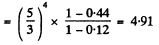
Q.259. Making use of Planck's formula, derive the expressions determining the number of photons per 1 cm3 of a cavity at a temperature T in the spectral intervals 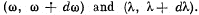
Ans. We use the formula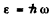
Then the number of photons in the spectral interval (ω, ω + dω) is
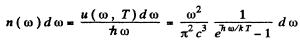
using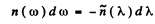
we get 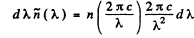
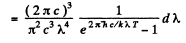
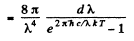
Q.260. An isotropic point source emits light with wavelength λ = 589 nm. The radiation power of the source is P = 10 W. Find:
(a) the mean density of the flow of photons at a distance r = = 2.0 m from the source;
(b) the distance between the source and the point at which the mean concentration of photons is equal to n = 100 cm -3.
Ans. (a) The mean density of the flow of photons at a distance r is
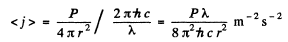
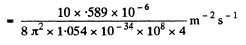
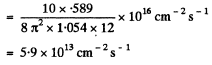
(b) If n(r) is the mean concentration (number per unit volume) of photons at a distance r form the source, then, since all photons are moving outwards with a velocity c, there is an outward flux of cn which is balanced by the flux from the source. In steady state, the two are equal and so

so 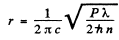
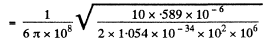
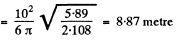

|
Explore Courses for JEE exam
|

|

















