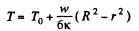Irodov Solutions: Transport Phenomena- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download

Q. 239. An ideal gas goes through a polytropic process. Find the polytropic exponent n if in this process the coefficient
 (a) of diffusion;
 (b) of viscosity;
 (c) of heat conductivity remains constant. 

Solution. 239.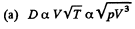 

Thus D remains constant in the process pV³ = constant

So polytropic index n = 3 

So η remains constant in the isothermal process

pV = constant, n = 1, here 

(c) Heat conductivity k = ηC_v and C_v is a constant for the ideal gas

Thus n = 1 here also,

Q. 240. Knowing the viscosity coefficient of helium under standard conditions, calculate the effective diameter of the helium atom. 

Solution. 240.  

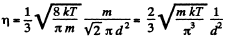
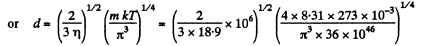
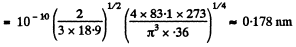
Q. 241. The heat conductivity of helium is 8.7 times that of argon (under standard conditions). Find the ratio of effective diameters of argon and helium atoms.

Solution. 241.  

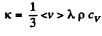
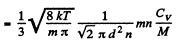
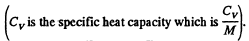 Now C_v is the same for all monoatomic  gases such as He and A. Thus

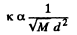
or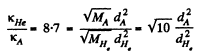  

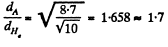
Q. 242. Under standard conditions helium fills up the space between two long coaxial cylinders. The mean radius of the cylinders is equal to R, the gap between them is equal to ΔR, with AR ≪ R. The outer cylinder rotates with a fairly low angular velocity o about the stationary inner cylinder. Find the moment of friction forces acting on a unit length of the inner cylinder. Down to what magnitude should the helium pressure be lowered (keeping the temperature constant) to decrease the sought moment of friction forces n = 10 times if ΔR = 6 mm? 

Solution. 242. In this case

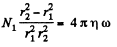
or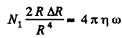 

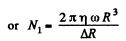
To decrease N₁,n times η must be decreased n times. Now η does not depend on pressure until the pressure is so low that the mean free path equals, 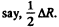 Then the mean free path is fixed and η  decreases with pressure. The mean free path equals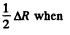

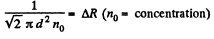
Corresponding pressure is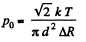 

The sought pressure is n times less 

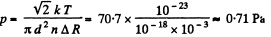
The answer is qualitative and depends on die choice 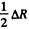  for the mean free path.

Q. 243. A gas fills up the space between two long coaxial cylinders of radii R₁ and R₂, with R₁ < R₂. The outer cylinder rotates with a fairly low angular velocity ω about the stationary inner cylinder. The moment of friction forces acting on a unit length of the inner cylinder is equal to N₁. Find the viscosity coefficient η of the gas taking into account that the friction force acting on a unit area of the cylindrical surface of radius r is determined by the formula σ = .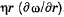 

Solution. 243. We neglect the moment of inertia of the gas in a shell. Then the moment of friction forces on a unit length of the cylinder must be a constant as a function of r.

So,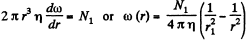  

and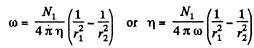  

Q. 244. Two identical parallel discs have a common axis and are located at a distance h from each other. The radius of each disc is equal to a, with a ≫ h. One disc is rotated with a low angular velocity ω relative to the other, stationary, disc. Find the moment of friction forces acting on the stationary disc if the viscosity coefficient of the gas between the discs is equal to η

Solution. 244. We consider two adjoining layers. The angular velocity gradient is ω/h. So the moment of the frictional force is

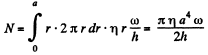
Q. 245.  Solve the foregoing problem, assuming that the discs are located in an ultra-rarefied gas of molar mass M, at temperature T and under pressure p.

Solution. 245. In the ultrararefled gas we must determine η by taking 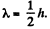 Then

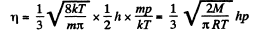
so,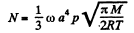  

Q. 246. Making use of Poiseuille's equation (1.7d), find the mass μ of gas flowing per unit time through the pipe of length l and radius a if constant pressures p₁  and p₂ are maintained at its ends.

Solution. 246. Take an infinitesimal section of length dx and apply Poiseuilles equation to this. Then

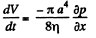
From the formula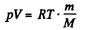 

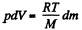
or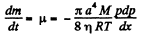  

This equation implies that if the flow is isothermal then 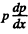  must be a constant and so equals  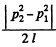 in magnitude.

Thus,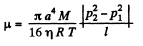 

Q. 247. One end of a rod, enclosed in a thermally insulating sheath, is kept at a temperature T₁ while the other, at T₂. The rod is composed of two sections whose lengths are l₁ and l₂ and heat conductivity coefficients x₁ and x₂. Find the temperature of the interface. 

Solution. 247. Let T = temperature of the interface.

Then heat flowing from left = heat flowing into right in equilibrium.

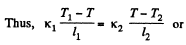
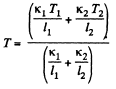
Q. 248. Two rods whose lengths are l₁ and 1₂ and heat conductivity coefficients x₁ and x₂  are placed end to end. Find the heat conductivity coefficient of a uniform rod of length l₁ + l₂ whose conductivity is the same as that of the system of these two rods. The lateral surfaces of the rods are assumed to be thermally insulated.

Solution. 248. We have

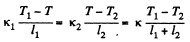
or using the previous result

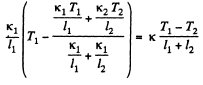
or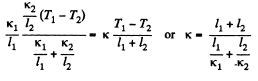 

Q. 249. A rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as x = α/T, where α is a constant. The ends of the rod are kept at temperatures T₁ and T₂. Find the function T (x), where x is the distance from the end whose temperature is T₁, and the heat flow density

Solution. 249. By definition the heat flux (per unit area) is

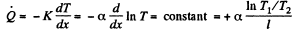
Integrating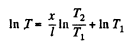   

where T₁ =  temperature at the end x = 0 

So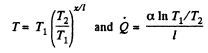  

Q. 250. Two chunks of metal with heat capacities C₁ and C₂ are interconnected by a rod of length l and cross-sectional area S and fairly low heat conductivity x. The whole system is thermally insulated from the environment. At a moment t = 0 the temperature difference between the two chunks of metal equals (ΔT)₀. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chunks as a function of time. 

Solution. 250. Suppose the chunks have temperatures 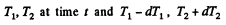  at time dt + t.

Then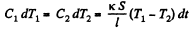 

Thus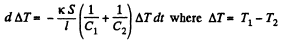 

Hence 

Q. 251. Find the temperature distribution in a substance placed between two parallel plates kept at temperatures T₁ and T₂. The plate separation is equal to 1, the heat conductivity coefficient of the substance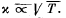 

Solution. 251.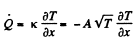  

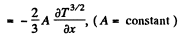
Thus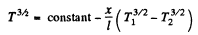  

or using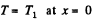  

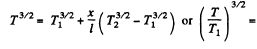
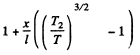
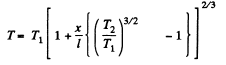
Q. 252. The space between two large horizontal plates is filled with helium. The plate separation equals l = 50 mm. The lower plate is kept at a temperature T₁ = 290 K, the upper, at T₂ = 330 K. Find the heat flow density if the gas pressure is close to standard. 

Solution. 252.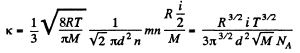 

Then from the previous problem

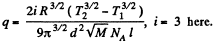
Q. 253. The space between two large parallel plates separated by a distance l = 5.0 mm is filled with helium under a pressure p = 1.0 Pa. One plate is kept at a temperature t₁ = 17°C and the other, at a temperature t₂ = 37°C. Find the mean free path of helium atoms and the heat flow density. 

Solution. 253. At this pressure and average temparature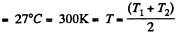 

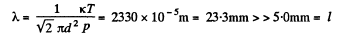
The gas is ultrathin and we write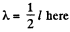 

Then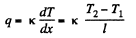  

where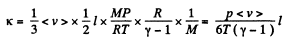 

and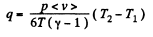 

where 

Q. 254. Find the temperature distribution in the space between two coaxial cylinders of radii R₁ and R₂  filled with a uniform heat conducting substance if the temperatures of the cylinders are constant and are equal to T₁  and T₂ respectively. 

Solution. 254. In equilibrium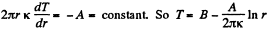 

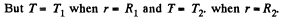
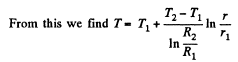
Q. 255. Solve the foregoing problem for the case of two concentric spheres of radii. R₁ and R₂ and temperatures T₁ and T₂. 

Solution. 255. In equilibrium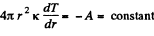 

Using T - T₁ when r = R₁ and T = T₂ when r = R₂,

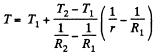
Q. 256. A constant electric current flows along a uniform wire with cross-sectional radius R and heat conductivity coefficient x. A unit volume of the wire generates a thermal power w. Find the temperature distribution across the wire provided the steady-state temperature at the wire surface is equal to T₀.

Solution. 256.  The heat flux vector is - k grad T and its divergence equals w. Thus

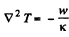
or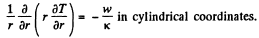 

or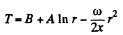 

Since T is finite at r = 0, A = 0. Also T = T₀ at r = R

so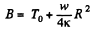  

Thus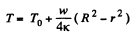 

r here is the distance from the axis of wire (axial radius). 

Q. 257. The thermal power of density w is generated uniformly inside a uniform sphere of radius R and heat conductivity coefficient x. Find the temperature distribution in the sphere provided the steady-state temperature at its surface is equal to T₀. 

Solution. 257.  Here again

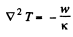
So in spherical polar coordinates,

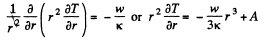
or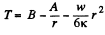  

Again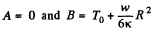  

so finally