Irodov Solutions: Universal Gravitation - 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 218. Two Earth's satellites move in a common plane along circular orbits. The orbital radius of one satellite r = 7000 km while that of the other satellite is Δr = 70 km less. What time interval separates the periodic approaches of the satellites to each other over the minimum distance?
Ans. 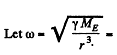 circular frequency o f the satellite in the outer orbit,
circular frequency o f the satellite in the outer orbit,
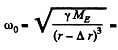 ircular frequency of the satellite in the inner orbit
ircular frequency of the satellite in the inner orbit
So, relative angular velocity 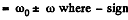 is to be taken when the satellites are moving in the same sense and + sign if they are moving in opposite sense.
is to be taken when the satellites are moving in the same sense and + sign if they are moving in opposite sense.
Hence, time between closest approaches
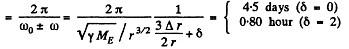
where δ is 0 in the first case and 2 in the second case.
Q. 219. Calculate the ratios of the following accelerations: the acceleration w1 due to the gravitational force on the Earth's surface, the acceleration w2 due to the centrifugal force of inertia on the Earth's equator, and the acceleration w3 caused by the Sun to the bodies on the Earth.
Ans. 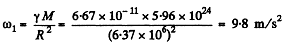
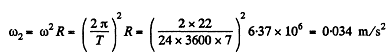
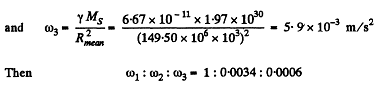
Q. 220. At what height over the Earth's pole the free-fall acceleration decreases by one per cent; by half?
Ans. Let h be the sought height in the first case, so
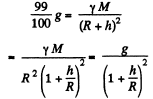
or 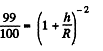
From the statement of the problem, it is obvious that in this case h<<R
Thus 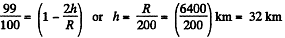
In the other case if h! be the sought height, than
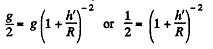
From the language o f the problem, in this case h' is not very small in comparison with R. Therefore in this case we cannot use the approximation adopted in the previous case.
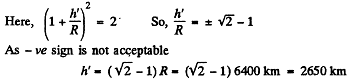
Q. 221. On the pole of the Earth a body is imparted velocity v0 directed vertically up. Knowing the radius of the Earth and the freefall acceleration on its surface, find the height to which the body will ascend. The air drag is to be neglected.
Ans. Let the mass of the body be m and let it go upto a height h.
From conservation of mechanical energy of the system
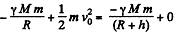
Using 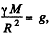 in above equation and on solving we get,
in above equation and on solving we get,
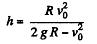
Q. 222. An artificial satellite is launched into a circular orbit around the Earth with velocity v relative to the reference frame moving translationally and fixed to the Earth's rotation axis. Find the distance from the satellite to the Earth's surface. The radius of the Earth and the free-fall acceleration on its surface are supposed to be known.
Ans. Gravitational pull provides the required centripetal acceleration to the satelite. Thus if h be the sought distance, we have
so, 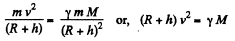
or, 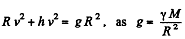
Hence 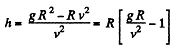
Q. 223. Calculate the radius of the circular orbit of a stationary Earth's satellite, which remains motionless with respect to its surface. What are its velocity and acceleration in the inertial reference frame fixed at a given moment to the centre of the Earth?
Ans. A satellite that hovers above the earth’s equator and corotates with it moving from the west to east with the diurnal angular velocity of the earth appears stationary to an observer on the earth. It is called geostationary. For this calculation we may neglect the annual motion of the earth as well as all other influences. Then, by Newton’s law,
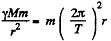
where M = mass of the earth, T = 86400 seconds = period of daily rotation of the earth and r = distance of the satellite from the centre of the earth. Then
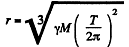
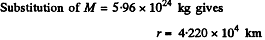
The instantaneous velocity with respect to an inertial frame fixed to the centre of the earth at that moment will be
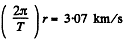
and the acceleration will be the centripetal acceleration.
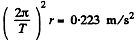
Q. 224. A satellite revolving in a circular equatorial orbit of radius R = 2.00-104 km from west to east appears over a certain point at the equator every τ = 11.6 hours. Using these data, calculate the mass of the Earth. The gravitational constant is supposed to be known.
Ans. We know from the previous problem that a satellite moving west to east at a distance R = 2-00 x 104 km from the centre of the earth will be revolving round the earth with an angular velocity faster than the earth’s diurnal angualr velocity. Let
ω = angular velocity of the satellite
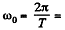 anuglar velocity of the earth. Then
anuglar velocity of the earth. Then
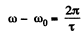
as the relative angular velocity with respect to earth. Now by Newton’s law
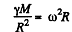
So, 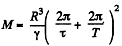
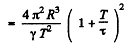
Substitution gives
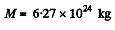
Q. 225. A satellite revolves from east to west in a circular equatorial orbit of radius R = 1.00.104 km around the Earth. Find the velocity and the acceleration of the satellite in the reference frame fixed to the Earth.
Ans. The velocity of the satellite in the inertial space fixed frame is 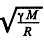 east to west . With respect to the Earth fixed frame, from the
east to west . With respect to the Earth fixed frame, from the 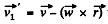 the velocity is
the velocity is
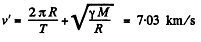
Here M is the mass of the earth and T is its period of rotation about its own axis.
It would be 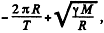 if the satellite were moving from west to east
if the satellite were moving from west to east
To find the acceleration we note the formula
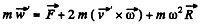
Here 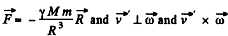 is directed towards the centre of the Earth.
is directed towards the centre of the Earth.
Thus 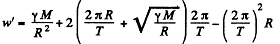
toward the earth’s rotation axis
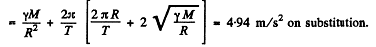
Q. 226. A satellite must move in the equatorial plane of the Earth close to its surface either in the Earth's rotation direction or against it. Find how many times the kinetic energy of the satellite in the latter case exceeds that in the former case (in the reference frame fixed to the Earth).
Ans. From the well known relationship between the velocities of a particle w.r.t a space fixed fram e (K) rotating frame 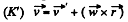
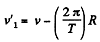
Thus kinetic energy of the satellite in the earth’s frame
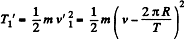
Obviously when the satellite moves in opposite sense comared to the rotation of the Earth its velocity relative to the same frame would be
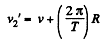
And kinetic energy
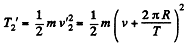 (2)
(2)
From (1) and (2)
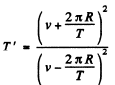 (3)
(3)
Now from Newton’s second law
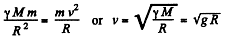 (4)
(4)
Using (4) and (3).
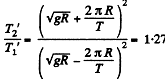 nearly (Using Appendices)
nearly (Using Appendices)
Q. 227. An artificial satellite of the Moon revolves in a circular orbit whose radius exceeds the radius of the Moon η times. In the process of motion the satellite experiences a slight resistance due to cosmic dust. Assuming the resistance force to depend on the velocity of the satellite as F = αv2, where a is α constant, find how long the satellite will stay in orbit until it falls onto the Moon's surface.
Ans. For a satellite in a circular orbit about any massive body, the following relation holds between kinetic, potential & total eneigy :
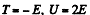 (1)
(1)
Thus since total mechanical energy must decrease due to resistance of the cosmic dust, the kintetic energy will increase and the satellite will 'fair, We see then, by work eneigy theorm
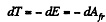
So, 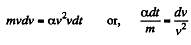
Now from Netow’s law at an arbitray radius r from the moon’s centre.
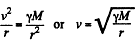
(M is the mass of the moon.) Then
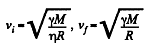
where R= moon’s radius. So
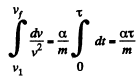
or, 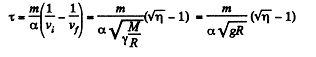
where g is moon’s gravity. The averaging implied by Eq. (1) (for noncircular orbits) makes the result approximate.
Q. 228. Calculate the orbital and escape velocities for the Moon. Compare the results obtained with the corresponding velocities for the Earth.
Ans. From Newton’s second law
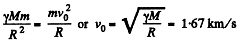 (1)
(1)
From conservation of mechanical energy
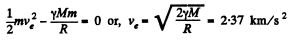 (2)
(2)
In Eq. (1) and (2), M and R are the mass of the moon and its radius. In Eq. (1) if M and R represent the mass of the earth and its radius, then, using appendices, we can easily get
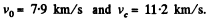
Q. 229. A spaceship approaches the Moon along a parabolic trajectory which is almost tangent to the Moon's surface. At the moment of the maximum approach the brake rocket was fired for a short time interval, and the spaceship was transferred into a circular orbit of a Moon satellite. Find how the spaceship velocity modulus increased in the process of braking.
Ans. In a parabolic orbit, E = 0
So 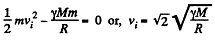
where M = mass of the Moon, R = its radius. (This is just the escape velocity.) On the other hand in orbit
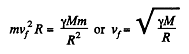
Thus 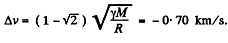
Q. 230. A spaceship is launched into a circular orbit close to the Earth's surface. What additional velocity has to be imparted to the spaceship to overcome the gravitational pull?
Ans. From 1.228 for the Earth surface
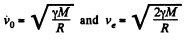
Thus the sought additional velocity
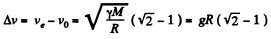
This ‘kick’ in velocity must be given along the direction of motion of the satellite in its orbit
Q. 231. At what distance from the centre of the Moon is the point at which the strength of the resultant of the Earth's and Moon's gravitational fields is equal to zero? The Earth's mass is assumed to be η = 81 times that of the Moon, and the distance between the centres of these planets n = 60 times greater than the radius of the Earth R.
Ans. Let r be the sought distance, then
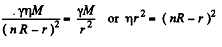
or 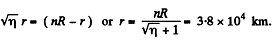
Q. 232. What is the minimum work that has to be performed to bring a spaceship of mass m = 2.0.103 k g from the surface of the Earth to the Moon?
Ans. Between the earth and the moon, the potential energy of the spaceship will have a maximum at the point where the attractions of the earth and the moon balance each other. This maximum RE. is approximately zero. We can also neglect the contribution of either body to the p.E. of the spaceship sufficiently near the other body. Then the minimum energy that must be imparted to the spaceship to cross the maximum of the P.E. is clearly (using E to denote the earth)
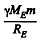
With this energy the spaceship will cross over the hump in the P.E. and coast down the hill of p.E. towards the moon and crashland on it. What the problem seeks is the minimum energy reguired for softlanding. That reguies the use of rockets to loving about the braking of the spaceship and since the kinetic energy of the gases ejected from the rocket will always be positive, the total energy required for softlanding is greater than that required for crashlanding. To calculate this energy we assume that the rockets are used fairly close to the moon when the spaceship has nealy attained its terminal velocity on the moon 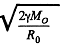 where M0 is the mass of the moon and R0 is its radius. In general dE = vdp and since the speed of the ejected gases is not less than the speed of the rocket, and momentum transfered to the ejected gases must equal the momentum of the spaceship the energy E of the gass ejected is not less than the kinetic energy of spaceship
where M0 is the mass of the moon and R0 is its radius. In general dE = vdp and since the speed of the ejected gases is not less than the speed of the rocket, and momentum transfered to the ejected gases must equal the momentum of the spaceship the energy E of the gass ejected is not less than the kinetic energy of spaceship
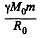
Addding the two we get the minimum work done on the ejected gases to bring about the softlanding.
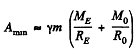
On substitution we get 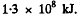
Q. 233. Find approximately the third cosmic velocity v3, i.e. the minimum velocity that has to be imparted to a body relative to the Earth's surface to drive it out of the Solar system. The rotation of the Earth about its own axis is to be neglected.
Ans. Assume first that the attraction of the earth can be neglected. Then the minimum velocity, that must be imparted to the body to escape from the Sun’s pull, is, as in 1*230, equal to 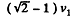
where 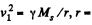 radius of the earth’s orbit, Ms - mass of the Sun.
radius of the earth’s orbit, Ms - mass of the Sun.
In the actual case near the earth, the pull of the Sun is small and does not change much over distances, which are several times the radius of the Earth. The velocity v3 in question is that which overcomes the earth’s pull with sufficient velocity to escape the Sun’s pull.
Thus
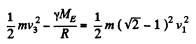
where R = radius of the earth, ME = mass of the earth.
Writing 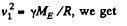
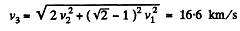
FAQs on Irodov Solutions: Universal Gravitation - 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. How does the universal gravitation equation relate to the motion of celestial bodies? |  |
| 2. How is the universal gravitation equation derived? |  |
| 3. What is the significance of the gravitational constant (G) in the universal gravitation equation? |  |
| 4. How does the distance between two objects affect the gravitational force between them? |  |
| 5. Is the universal gravitation equation applicable only to celestial bodies? |  |

|
Explore Courses for JEE exam
|

|

















