Irodov Solutions: Wave Properties of Particles. Schrodinger Equation- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.49. Calculate the de Broglie wavelengths of an electron, proton, and uranium atom, all having the same kinetic energy 100 eV.
Ans. The kinetic eneigy is nonrelativistic in all three cases. Now
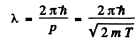
using 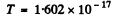 Joules, we get
Joules, we get
λe = 122.6 pm
λp = 2.86 pm
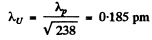
(where we have used a mass number of 238 for the U nucleus).
Q.50. What amount of energy should be added to an electron to reduce its de Broglie wavelength from 100 to 50 pm?
Ans. From
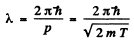
we find 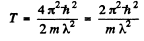
Thus 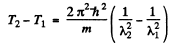
Substitution gives 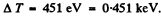
Q.51. A neutron with kinetic energy T = 25 eV strikes a stationary deuteron (heavy hydrogen nucleus). Find the de Broglie wavelengths of both particles in the frame of their centre of inertia.
Ans. We shall use M0 = 2Mn. The CM is moving with velocity
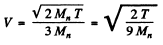
with respect to the Lab frame. In the CM frame the velocity of neutron is
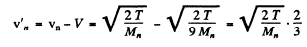
and 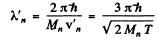
Substitution gives 
Since the momenta are equal in the CM frame the de Broglie wavelengths will also be equal. If we do not assume 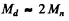 we shall get
we shall get
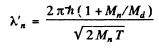
Q.52. Two identical non-relativistic particles move at right angles to each other, possessing de Broglie wavelengths λ1 and λ2. Find the de Broglie wavelength of each particle in the frame of their centre of inertia.
Ans. If 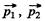 are the momenta o f the two particles then their momenta in the CM frame will be
are the momenta o f the two particles then their momenta in the CM frame will be
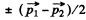 as the particle are identical.
as the particle are identical.
Hence their de Broglie wavelength will be
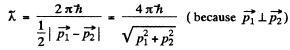

Q.53. Find the de Broglie wavelength of hydrogen molecules, which corresponds to their most probable velocity at room temperature.
Ans. In thermodynamic equilibrium, Maxwell’s velocity distribution law holds :
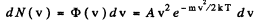
φ (v) is maximum when
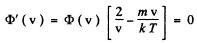
The difines the most probable velocity,

The de Broglie wavelength of H molecules with the most probable velocity is
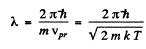
Substituting the appropriate value especially
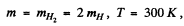 we get
we get
λ = 126 pm
Q.54. Calculate the most probable de Broglie wavelength of hydrogen molecules being in thermodynamic equilibrium at room temperature.
Ans. To find the most probable de Broglie wavelength of a gas in thermodynamic equilibrium we determine the distribution is λ corresponding to Maxwellian velocity distribution.
It is given by
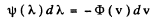
(where - sign takes account of the fact that λ decreaes as v increases). Now
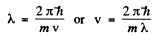
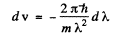
Thus 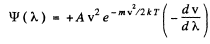
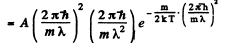
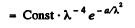
where 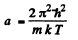
This is maximum when

or 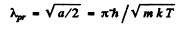
Using the result of the previous problem it is
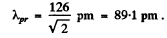
Q.55. Derive the expression for a de Broglie wavelength λ of a relativistic particle moving with kinetic energy T. At what values of T does the error in determining λ using the non-relativistic formula not exceed 1% for an electron and a proton?
Ans. For a relativistic particle
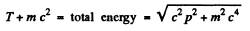
Squaring 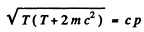
Hence 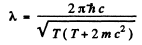
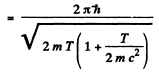
If we use nonrelativistic formula,
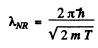
SO 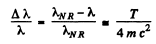
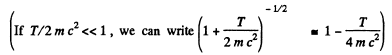
Thus 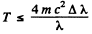 i,f the error is less than Δλ
i,f the error is less than Δλ
For electron the error is not more than 1 % if
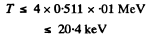
For a proton, the error is not more than 1 % if
T ≤ 4 X 938 X 0.01 MeV
i.e. T ≤ 37.5 MeV.
Q.56. At what value of kinetic energy is the de Broglie wavelength of an electron equal to its Compton wavelength?
Ans. The de Broglie wavelength is
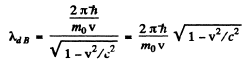
and the Compton wavelength is
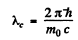
The two are equal if 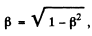

or 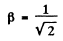
The corresponding kinetic energy is
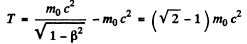
Here m0 is th rest mass of the particle (here an electron).
Q.57. Find the de Broglie wavelength of relativistic electrons reaching the anticathode of an X-ray tube if the short wavelength limit of the continuous X-ray spectrum is equal to λsh = 10.0 pm?
Ans. For relativistic electrons, the formula for the short wavelength limit of X - rays will be
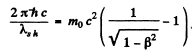
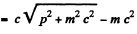
or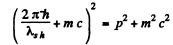
or 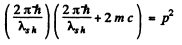
or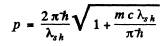
Hence 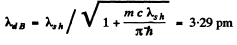
Q.58. A parallel stream of monoenergetic electrons falls normally on a diaphragm with narrow square slit of width b = 1.0 μm. Find the velocity of the electrons if the width of the central diffraction maximum formed on a screen located at a distance l = 50 cm from the slit is equal to Δx = 0.36 mm.
Ans. he first minimum in a Fraunhofer diffraction is given by (b is the width of the slit)
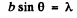
Here
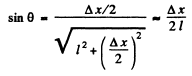
Thus 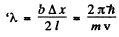
so 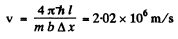
Q.59. A parallel stream of electrons accelerated by a potential difference V = 25 V falls normally on a diaphragm with two narrow slits separated by a distance d = 50μm. Calculate the distance between neighbouring maxima of the diffraction pattern on a screen located at a distance l = 100 cm from the slits.
Ans. From the Young slit foimula
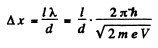
Substitution gives
Q.60. A narrow stream of monoenergetic electrons falls at an angle of incidence θ = 30° on the natural facet of an aluminium single crystal. The distance between the neighbouring crystal planes parallel to that facet is equal to d = 0.20 nm. The maximum mirror reflection is observed at a certain accelerating voltage V0. Find Vo, if the next maximum mirror reflection is known to be observed when the accelerating voltage is increased η = 2.25 times.
Ans. From Bragg’s law, for the first case
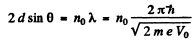
where no is an unknown integer/For the next higher voltage

Thus 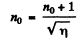
or 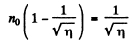
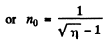
Going back we get
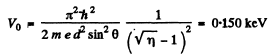
Note : In the Bragg’s formula, θ is the glancing angle and not the angle of incidence. We have obtained correct result by taking θ to be the glancing angle. If θ is the angle of incidence, then the glancing angle will be 90 - θ. Then the final answer will be smaller by a factor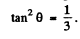
Q.61. A narrow beam of monoenergetic electrons falls normally on the surface of a Ni single crystal. The reflection maximum of fourth order is observed in the direction forming an angle θ = 55° with the normal to the surface at the energy of the electrons equal to T = 180 eV. Calculate the corresponding value of the interplanar distance.
Ans. Path difference is
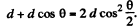
Thus for reflection maximum of the kth order
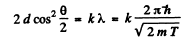
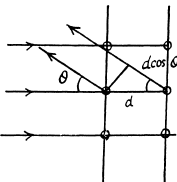
Hence 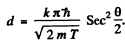
substitution with k = 4gives
d = 0.232
Q.62. A narrow stream of electrons with kinetic energy T = 10 keV passes through a polycrystalline aluminium foil, forming a system of diffraction fringes on a screen. Calculate the interplanar distance corresponding to the reflection of third order from a certain system of crystal planes if it is responsible for a diffraction ring of diameter D = 3.20 cm. The distance between the foil and the screen is l = 10.0 cm.
Ans. See the analogous problem with X - rays (5.156) The glancing angle is obtained from
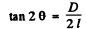
where D = diameter of the ring, l = distance from the foil to the screen.
Then for the third order Bragg reflection
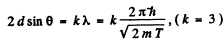
Thus 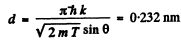
Q.63. A stream of electrons accelerated by a potential difference V falls on the surface of a metal whose inner potential is V1 = 15 V. Find:
(a) the refractive index of the metal for the electrons accelerated by a potential difference V = 150 V;
(b) the values of the ratio V/Vt at which the refractive index differs from unity by not more than η = 1.0%.
Ans. Inside the metal, there is a negative potential energy of - eVi}. (This potential energy prevents electrons from leaking out and can be measured in photoelectric effect etc.) An electron whose K.E. is eV outside the metal w ill find its K.E. increased to e (V + Vi) in th e metal. Then
(a) de Broglie wavelength in the metal
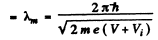
Also de Broglie wavelength in vacuum
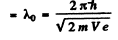
Hence refractive index 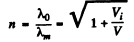
Substituting we get 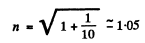
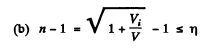
then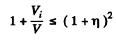
or 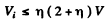
or 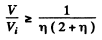
For 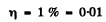
we get 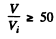
Q.64. A particle of mass m is located in a unidimensional square potential well with infinitely high walls. The width of the well is equal to l. Find the permitted values of energy of the particle taking into account that only those states of the particle's motion are realized for which the whole number of de Broglie half-waves are fitted within the given well.
Ans. The energy inside the well is all kinetic if energy is measured from the value inside. We require
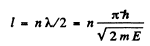
or 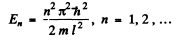
Q.65. Describe the Bohr quantum conditions in terms of the wave theory: demonstrate that an electron in a hydrogen atom can move only along those round orbits which accommodate a whole number of de Broglie waves.
Ans. The Bohr condition
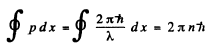
For the case when λ is constant (for example in circular orbits) this means
2nr = nλ
Here r is the radius of the circular orbit.
FAQs on Irodov Solutions: Wave Properties of Particles. Schrodinger Equation- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is the Schrodinger equation and how is it related to wave properties of particles? |  |
| 2. Can the Schrodinger equation be used to describe both particles and waves? |  |
| 3. How does the Schrodinger equation explain the quantization of energy levels in atoms? |  |
| 4. Can the Schrodinger equation be solved analytically for all physical systems? |  |
| 5. How does the Schrodinger equation relate to the wave-particle duality of particles? |  |


















