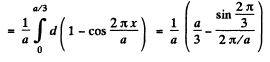Irodov Solutions: Wave Properties of Particles. Schrodinger Equation- 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.66. Estimate the minimum errors in determining the velocity of an electron, a proton, and a ball of mass of 1 mg if the coordinates of the particles and of the centre of the ball are known with uncertainly 1µm.
Ans. From the uncertainty principle (Eqn. (6.2b))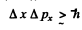
Thus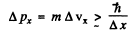
or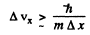
For an electron this means an uncertainty in velocity of 116 m/s if 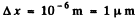
For a proton Δvx = 6.3 cm/s
For a ball Δvx = 1 x 10-20cm/s
Q.67. Employing the uncertainty principle, evaluate the indeterminancy of the velocity of an electron in a hydrogen atom if the size of the atom is assumed to be l = 0.10 nm. Compare the obtained magnitude with the velocity of an electron in the first Bohr orbit of the given atom.
Ans. As in the previous problem
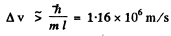
The actual velocity v1 has been calculated in problem 6.21. It is
v1 = 2.21 x 106 m/s
Thus 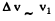 (They are of the same order of magnitude)
(They are of the same order of magnitude)
Q.68. Show that for the particle whose coordinate uncertainty is Δx = λ/2π, where λ is its de Broglie wavelength, the velocity uncertainty is of the same order of magnitude as the particle's velocity itself.
Ans. If 
Thus 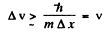
Thus Δv is of the same order as v.
Q.69. A free electron was initially confined within a region with linear dimensions l = 0.10 nm. Using the uncertainty principle, evaluate the time over which the width of the corresponding train of waves becomes η = 10 times as large.
Ans. Initial uncertainty 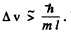 With this incertainty the wave train will spread out to a distance ηl long in time
With this incertainty the wave train will spread out to a distance ηl long in time
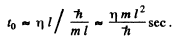
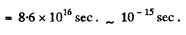
Q.70. Employing the uncertainty principle, estimate the minimum kinetic energy of an electron confined within a region whose size is l = 0.20 nm.
Ans. Clearly 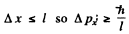
Now 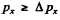 and so
and so
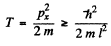
Thus 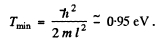
Q.71. An electron with kinetic energy T ≈ 4 eV is confined within a region whose linear dimension is l = 1 µm. Using the uncertainty principle, evaluate the relative uncertainty of its velocity.
Ans. The momentum the electron is 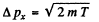
Uncertainty in its momentum is
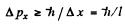
Hence relative uncertainty
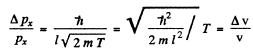
Substitution gives
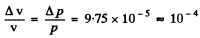
Q.72. An electron is located in a unidimensional square potential well with infinitely high walls. The width of the well is l. From the uncertainty principle estimate the force with which the electron possessing the minimum permitted energy acts on the walls of the well.
Ans. By uncertainty principle, the uncertainty in momentum
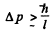
For the ground state, we expect 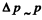 so
so
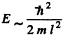
The force excerted on the wall can be obtained most simply from
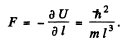
Q.73. A particle of mass m moves in a unidimensional potential field U = kx2/2 (harmonic oscillator). Using the uncertainty principle, evaluate the minimum permitted energy of the particle in that field.
Ans. We write
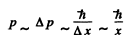
i.e. all four quantities are of the same order of magnitude. Then
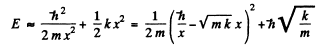
Thus we get an equilibrium situation (E = minimum) when
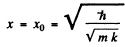
and then 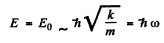
Quantum mechanics gives
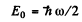
Q.74. Making use of the uncertainty principle, evaluate the minimum permitted energy of an electron in a hydrogen atom and its corresponding apparent distance from the nucleus.
Ans. Hence we write
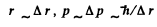
Then
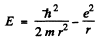
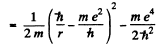
Hence 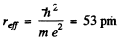 for the equilibrium state.
for the equilibrium state.
and then 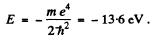
Q.75. A parallel stream of hydrogen atoms with velocity v = 600 m/s falls normally on a diaphragm with a narrow slit behind which a screen is placed at a distance l = 1.0 m. Using the uncertainty principle, evaluate the width of the slit S at which the width of its image on the screen is minimum.
Ans. Suppose the width of the slit (its extension along they - axis) is δ. Then each electron has an uncertainty 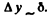 This translates to an uncertainty
This translates to an uncertainty
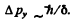 We must therefore have
We must therefore have
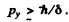
For the image, hrodening has two sources.
We write
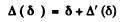
where Δ' is the width caused by the spreading of electrons due to their transverse momentum.
We have
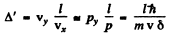
Thus
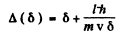
For large 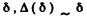 and quantum effect is unimportant. For small δ, quantum effects are large. But A (δ) is minimum when
and quantum effect is unimportant. For small δ, quantum effects are large. But A (δ) is minimum when
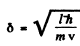
as we see by completing the square. Substitution gives
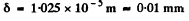
Q.76. Find a particular solution of the time-dependent Schrodinger equation for a freely moving particle of mass m.
Ans. The Schrodinger equation in one dimension for a free particle is
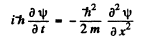
we write 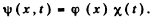 Then
Then
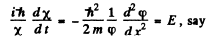
Then 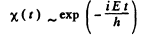
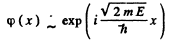
E must be real and positive if φ(x) is to be bounded everywhere. Then
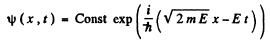
This particular solution describes plane waves.
Q.77. A particle in the ground state is located in a unidimensional square potential well of length 1 with absolutely impenetrable walls (0 < x < l). Find the probability of the particle staying within a region 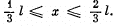
Ans. We look for the solution of Schrodinger eqn. with
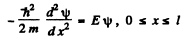 (1)
(1)
The boundary condition of impenetrable walls means

The solution of (1) is
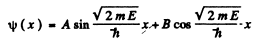
Then 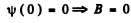
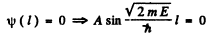
A = 0 so

Hence 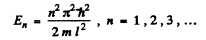
Thus the ground state wave function is
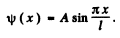
We evaluate A by nomalization
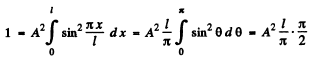
Thus 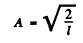
Finally, the probability P for the particle to lie in 
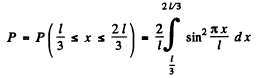
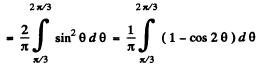
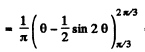
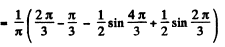
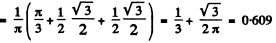
Q.78. A particle is located in a unidimensional square potential well with infinitely high walls. The width of the well is 1. Find the normalized wave functions of the stationary states of the particle, taking the midpoint of the well for the origin of the x coordinate.
Ans.
Here 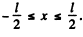 . Again wc have
. Again wc have
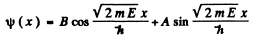
Then the boundary condition 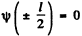
gives 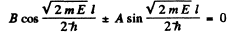
There are two cases.
(1) 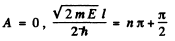
gives even solution. Here
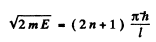
and 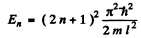
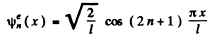
n = 0 , 1 , 2 , 3 , . . .
This solution is even under x → - x .
(2) B = 0 , 
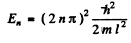
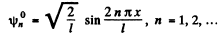 This solution is odd.
This solution is odd.
Q.79. Demonstrate that the wave functions of the stationary states of a particle confined in a unidimensional potential well with infinitely high walls are orthogonal, i.e. they satisfy the condition
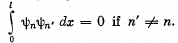
Here l is the width of the well, n are
integers.
Ans. The wave function is given in 6.77. We see that
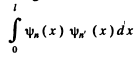
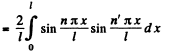
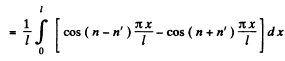
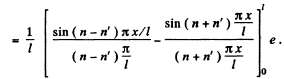
If n = n', this is zero as n and n' are integers.
Q.80. An electron is located in a unidimensional square potential well with infinitely high walls. The width of the well equal to 1 is such that the energy levels are very dense. Find the density of energy levels dN/dE, i.e. their number per unit energy interval, as a function of E. Calculate dN/dE for E = 1.0 eV if l = 1.0 cm.
Ans.
We have found that 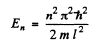
Let N (E) = number of states upto E. This number is n. The number of states upto E + dE is N( E + dE) = N(E ) + d N ( E ) . Then dN (E ) - 1 and
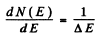
where ΔE = difference in energies between the nth & (n + 1)th level
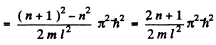
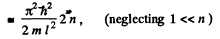
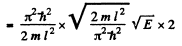
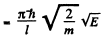
Thus
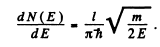
For the given case this gives 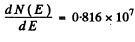 levels per eV
levels per eV
Q.81. A particle of mass m is located in a two-dimensional square potential well with absolutely impenetrable walls. Find:
(a) the particle's permitted energy values if the sides of the well are l1, and l2;
(b) the energy values of the particle at the first four levels if the well has the shape of a square with side l.
Ans.
(a) Here the schroditiger equation is
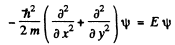
we take the origin at one of the comers of the rectangle where the particle can lie. Then the wave function must vanish for
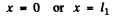
or y = 0 or y = l2 .
we look for a solution in the form
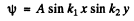
cosines are not permitted by the boundary condition. Then
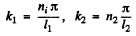
and 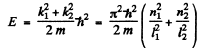
Here n1, n2 are nonzero integers,
(b) If 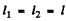 then
then
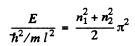
1st level :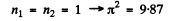
2nd level :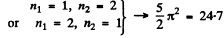
3rd level :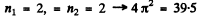
4th level :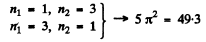
Q.82. A particle is located in a two-dimensional square potential well with absolutely impenetrable walls (0 < x < a, 0 < y < b).
Find the probability of the particle with the lowest energy to be located within a region 0 < x < a/3.
Ans.
The wave function for the ground state is
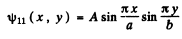
we find A by normalization
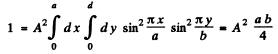
Thus 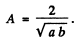
Then the requisite probability is
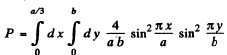
 on doing the y integral
on doing the y integral