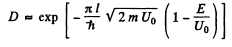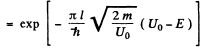Irodov Solutions: Wave Properties of Particles. Schrodinger Equation- 3 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.83. A particle of mass m is located in a three-dimensional cubic potential well with absolutely impenetrable walls. The side of the cube is equal to a. Find:
(a) the proper values of energy of the particle;
(b) the energy difference between the third and fourth levels;
(c) the energy of the sixth level and the number of states (the degree of degeneracy) corresponding to that level.
Ans. We proceed axactly as in (6.81). The wave function is chosen in the form
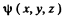 = A sin k1x sin k2 y sin k3 z .
= A sin k1x sin k2 y sin k3 z .
(The origin is at one comer of the box and the axes of coordinates are along the edges.) The boundary conditions are that 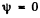 for
for
x = 0, x = a, y = 0, y = a, z = 0, z = a
This gives
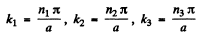
The energy eigenvalues are
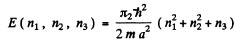
The first level is (1, 1, 1). The second has (1, 1, 2), (1, 2, 1) & (2, 1, 1). The third level is (1, 2, 2) or (2, 1, 2) or (2, 2, 1). Its eneigy is
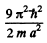
The fourth energy level is (1, 1, 3) or (1, 3, 1) or (3, 1, 1)
Its eneigy is 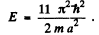
(b) Thus 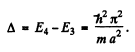
(c) The fifth level is (2, 2, 2). The sixth level is (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)
Its eneigy is
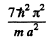
and its degree of degeneracy is 6 (six).
Q.84. Using the Schrodinger equation, demonstrate that at the point where the potential energy U (x) of a particle has a finite discontinuity, the wave function remains smooth, i.e. its first derivative with respect to the coordinate is continuous.
Ans. We can for definiteness assume that the discontinuity occurs at the point x = 0. Now the schrodinger equation is
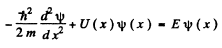
We integrate this equation around x = 0 i.e., from 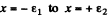 where
where 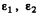 are small positive numbers. Then
are small positive numbers. Then
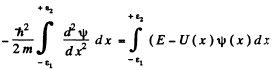
or 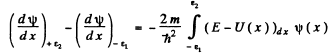
Since the potential and the energy E are finite and ψ(x) is bounded by assumption, the integral on the right exists and 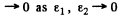
Thus 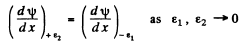
So 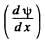 is continuous at x = 0 (the point where U (x) has a finite jump discontinuity.)
is continuous at x = 0 (the point where U (x) has a finite jump discontinuity.)
Q.85. A particle of mass m is located in a unidimensional potential field U (x) whose shape is shown in Fig. 6.2, where U(0) =  . Find:
. Find:
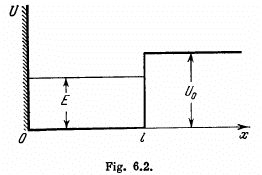
(a) the equation defining the possible values of energy of the particle in the region E < U0; reduce that equation to the form
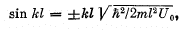
where 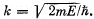 Solving this equation by graphical means, demonstrate that the possible values of energy of the particle form a discontinuous spectrum;
Solving this equation by graphical means, demonstrate that the possible values of energy of the particle form a discontinuous spectrum;
(b) the minimum value of the quantity l2U0 at which the first energy level appears in the region E < U0. At what minimum value of l2Uo does the nth level appear?
Ans.
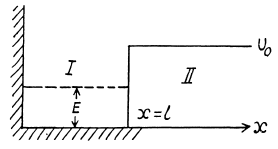
(a) Starting from the Schrodinger equation in the regions l & II
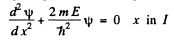 (1)
(1)
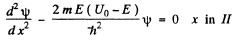 (2)
(2)
where U0 > E > 0 , we easily derive the solutions in I & II
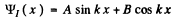 (3)
(3)
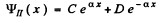 (4)
(4)
where 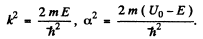
The boundary conditions are
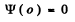 (5)
(5)
and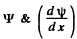 are continuous at x = /, and ψ must vanish at x = +
are continuous at x = /, and ψ must vanish at x = + 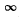 .
.
Then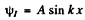
and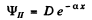
so 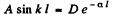
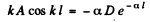
From this we get
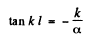
or 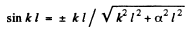
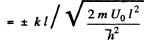
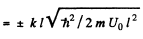 (6)
(6)
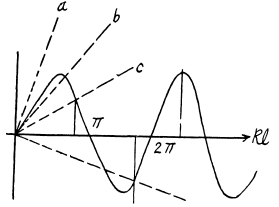
Plotting the left and right sides of this equation we can find the points at which the straight lines cross the sine curve. The roots of the equation corresponding to the eigen values of energy Ei and found from the inter section points (kl)i , for which tan (kl)i < 0 (i.e. 2nd & 4th and other even quadrants). It ii seen that bound states do not always exist. For the first bound state to appear (refer to the line (b) above)
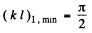
(b) Substituting, we get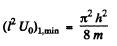
as the condition for the appearance of the first bound state. The second bound state will appear when Id is in the fourth quadrant The magnitude of the slope of the straight line must then be less than

Corresponding to 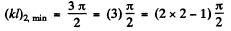
For n bound states, it is easy to convince one self that the slope of the appropriate straight line (upper or lower) must be less than
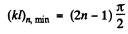
Then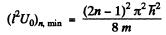
Do not forget to note that for large n both + and - signs in the Eq. (6) contribute to solutions.
Q.86. Making use of the solution of the foregoing problem, determine the probability of the particle with energy E = U0/2 to be located in the region 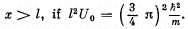
Ans.
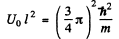
and 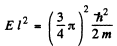
or 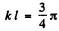
It is easy to check that the condition of the boud state is satisfied. Also
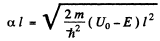
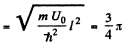
Then from the previous problem
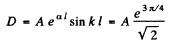
By normalization
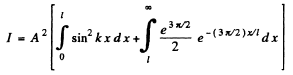
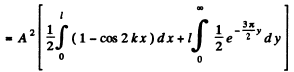
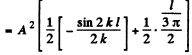
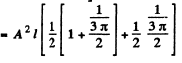
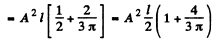
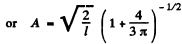
The probability of the particle to be located in the region x > l is
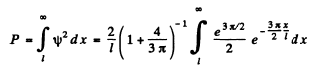
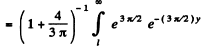
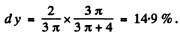
Q.87. Find the possible values of energy of a particle of mass m located in a spherically symmetrical potential well U (r) = 0 for r < ro and U (r) = 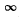 for r = r0, in the case when the motion of the particle is described by a wave function ψ(r) depending only on r.
for r = r0, in the case when the motion of the particle is described by a wave function ψ(r) depending only on r.
Instruction. When solving the Schrodinger equation, make the substitution ψ(r) = x (r)/r.
Ans. The Schrodinger equation is
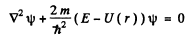
when ψ depends on r only,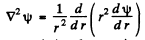
If we put 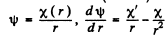
and 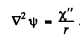 Thus we get
Thus we get
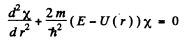
The solution is 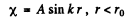
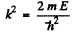
and 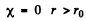
(For r < r0 we have rejected a term 5 cos k r as it does not vanish at r = 0). Continuity of the wavefunction at r = r0 requires
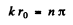
Hence 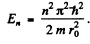
Q.88. From the conditions of the foregoing problem find:
(a) normalized eigenfunctions of the particle in the states for which ψ(r) depends only on r;
(b) the most probable value rpr for the ground state of the particle and the probability of the particle to be in the region r < rpr.
Ans. (a) The nomalized wave functions are obtained from the normalization
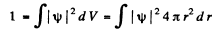
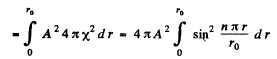
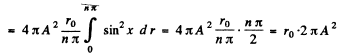
Hence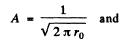
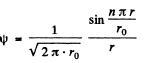
(b) The radial probability distribution function is
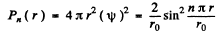
For the ground state n = 1
so 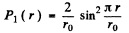
By inspection this is maximum for 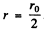 . Thus
. Thus 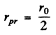
The probability for the particle to be found in the region r < rpr is clearly 50 % as one can immediately see from a graph of sin2x.
Q.89. A particle of mass m is located in a spherically symmetrical potential well U (r) = 0 for r < r0 and U (r) = U0 for r >
(a) By means of the substitution ψ(r) = x(r)/r find the equation defining the proper values of energy E of the particle for E < U0, when its motion is described by a wave function ψ(r) depending only on r. Reduce that equation to the form
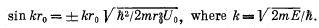
(b) Calculate the value of the quantity 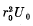 at which the first level appears.
at which the first level appears.
Ans. If we put 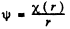
the equation for X(r) has the from 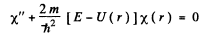
which can be written as 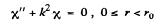
and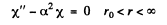
where 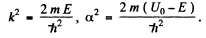
The boundary condition is
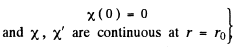
These are exactly same as in the one dimensional problem in problem (6.85) Wc therefore omit further details
Q.90. The wave function of a particle of mass in in a unidimensional potential field U (x) = kx2/2 has in the ground state the form ψ(x) = Ae-αx2, where A is a normalization factor and a is a positive constant. Making use of the Schrodinger equation, find the constant a and the energy E of the particle in this state.
Ans. The Schrodinger equation is 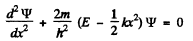
We are given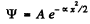
Then 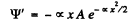
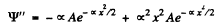
Substituting we find that following equation must hold

since 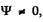 the bracket must vanish identicall. This means that the coefficient of x2 as well the term independent of x must vanish. We get
the bracket must vanish identicall. This means that the coefficient of x2 as well the term independent of x must vanish. We get
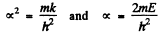
Putting k/m = ω2, this leads to 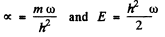
Q.91. Find the energy of an electron of a hydrogen atom in a stationary state for which the wave function takes the form ψ(r) = A (1 + ar) e-αr, where A, a, and α are constants.
Ans. The Schrodinger equation for the problem in Gaussian units
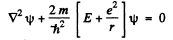
In MKS units we should read 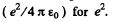
we put 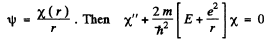 (1)
(1)
We are given that 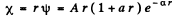
so 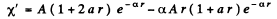
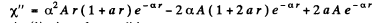
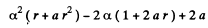
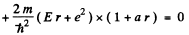
Equating the coefficients of r2, r, and constant term to zero we get
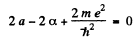 (2)
(2)
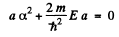 (3)
(3)
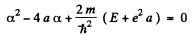 (4)
(4)
From (3) either a = 0, 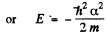
In the first case 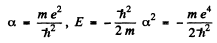
This state is the ground state.
It n the second, case 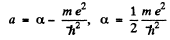
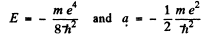
This state is one with n = 2 (2s).
Q.92. The wave function of an electron of a hydrogen atom in the ground state takes the form ψ(r) = Ae-r/r1, where A is a certain constant, r1 is the first Bohr radius. Find: (a) the most probable distance between the electron and the nucleus;
(b) the mean value of modulus of the Coulomb force acting on the electron;
(c) the mean value of the potential energy of the electron in the field of the nucleus.
Ans. We first find A by normalization
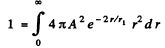
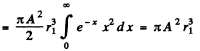
since the integral has the value 2.
Thus 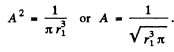
(a) The most probable distance rpr is that value of r for which
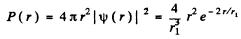
is maximum. This requires
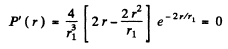
or 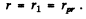
(b) The coulomb force being given by 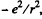 , the mean value o f its modulus is
, the mean value o f its modulus is
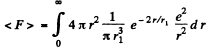
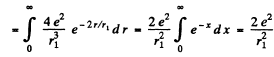
In MKS units we should read 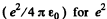
(c)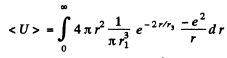
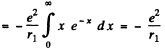
In MKS units we should read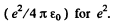
Q.93. Find the mean electrostatic potential produced by an electron in the centre of a hydrogen atom if the electron is in the ground state for which the wave function is ψ(r) = Ae-r/r1, where A is a certain constant, r1 is the first Bohr radius.
Ans. We find A by normalization as above. We get
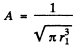
Then the electronic charge density is
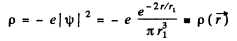
The potential 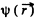 due to this charge density is
due to this charge density is
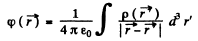
so at the origin 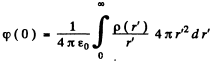
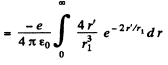
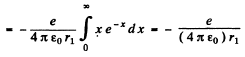
Q.94. Particles of mass m and energy E move from the left to the potential barrier shown in Fig. 6.3. Find:
(a) the reflection coefficient R of the barrier for E > U0;
(b) the effective penetration depth of the particles into the region x > 0 for E < Uo, i.e. the distance from the barrier boundary to the point at which the probability of finding a particle decreases e-fold.
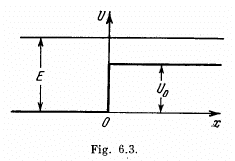
Ans. (a) We start from the Schrodinger equation 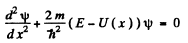
which we write as 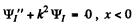
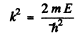
and 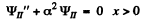
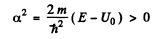
It is convenient to look for solutions in the form
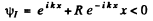
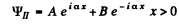
In region I (x < 0), the amplitude of 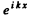 is written as unity by convention. In II we expect only a transmitted wave to the right, B = 0 then. So
is written as unity by convention. In II we expect only a transmitted wave to the right, B = 0 then. So
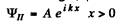
The boundary conditions follow from the continuity of 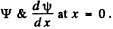
1 + R = A
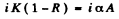
Then 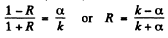
The reflection coefficient is the absolute square of R :
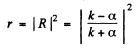
(b) In this case 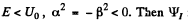 is unchanged in form but
is unchanged in form but
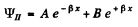
we must have B = 0 since otherwise ψ(x) will become unbounded as 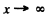 Finally
Finally
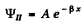
Inside the barrier, the particle then has a probability density equal to
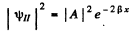
This decreases to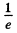 of its value in
of its value in
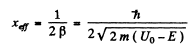
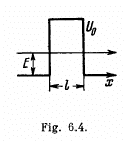
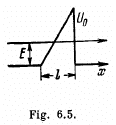
Q.95. Employing Eq. (6.2e), find the probability D of an electron with energy E tunnelling through a potential barrier of width l and height U0 provided the barrier is shaped as shown:
(a) in Fig. 6.4;
(b) in Fig. 6.5.
Ans. The formula is
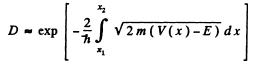
Here V(x2) = V(x1) = E and V(x) >E in the region x2 > x > x1.
(a) For the problem, the integral is trivial
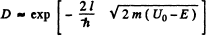
(b) We can without loss of generality take x = 0 at the point the potential begins to climb. Then
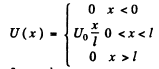
Then 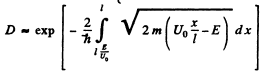
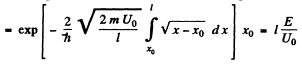
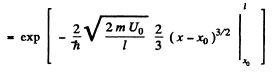
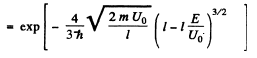
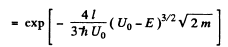
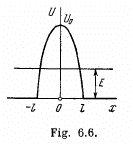
Q.96. Using Eq. (6.2e), find the probability D of a particle of mass m and energy E tunnelling through the potential barrier shown in Fig. 6.6, where U(x) = U0(1 — x2/l2).
Ans. The potential is 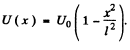 The turning points are
The turning points are
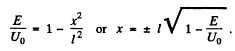
Then 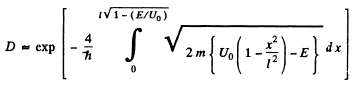
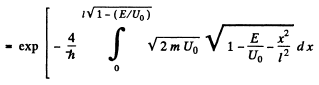
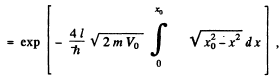
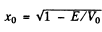
The integral is
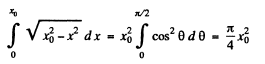
Thus