JEE Advanced (Fill in the Blanks): Matrices & Determinants | Chapter-wise Tests for JEE Main & Advanced PDF Download

Fill in the Blanks

Q. 1. 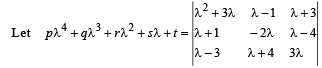  be an identity in λ , where p, q, r, s and t are constants. 

Then, the value of t is .................                       (1981 - 2 Marks)

Ans. t = 0

Solution. As given equation is an identity in λ, it must be true for all values of λ.

∴ For λ = 0 also. Putting λ = 0 we get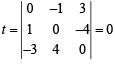 

Q. 2. The solution set of the equation 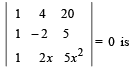  ..................      (1981 - 2 Marks)

Ans. x = –1, 2

Solution. Given equation is,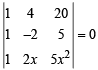 

Clearly on expanding the det. we will get a quadratic equation in x.

∴ It has 2 roots. We observe that R3 becomes identical to R₁ if x = 2. thus at x = 2 ⇒ Δ = 0
∴ x = 2 is a root of given eq.
Similarly R₃ becomes identical to R₂ if x = – 1. thus at x = – 1 Δ D = 0
∴ x = – 1 is a root of given eq.
Hence equation has roots as –1 and 2.

Q. 3. A determinant is chosen at random from the set of all determinants of order 2 with elements 0 or 1 only. The probability that the value of determinant chosen is  positive is ..................      (1982 - 2 Marks)

Ans. 3/16
Solution. With 0 and 1 as elements there are 2 × 2 × 2 × 2 = 16 determinants of order 2 × 2 out of which only 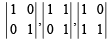  are the three det whose value is +ve.
∴ Req. prob. = 3/16

Q. 4. Given that x = -9 is a root of 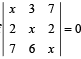  the other two roots are  ................. and  ..............     (1983 - 2 Marks)

Ans. 2, 7

Solution.

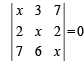
Operating R₁ → R₁ + R₂ + R₃ we get

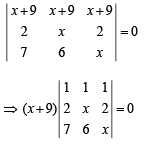
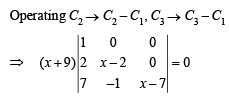
Expanding along R₁
⇒(x + 9) (x – 2) (x – 7) = 0
⇒ x = – 9, 2, 7
∴ Other roots are 2 and 7.

 
Q. 5. The system  of equations

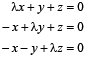
Will have a non-zero solution if real values of  l are given by ..................   (1984 - 2 Marks)

Ans. λ = 0

Solution. The given homogeneous system of equations will have non zero solution if D = 0

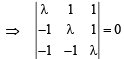
⇒ λ (λ² + 1) – 1 (–λ + 1) + 1 (1 + λ) = 0 ⇒ λ³ + 3λ = 0
⇒ λ (λ² + 3) = 0, but λ² + 3 ≠ 0 for real λ ⇒ λ = 0

Q. 6. The value of the determinant 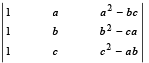is ..................   (1988 - 2 Marks)

Ans. 0

Solution.

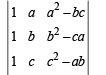
Operating R₁→ R₁ –  R₂;  R₂→  R₂ – R₃

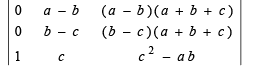
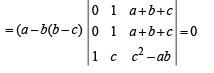
Q. 7. For positive numbers x, y and z, the numerical value of the determinant 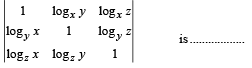         (1993 -  2 Marks)

Ans. 0

Solution. Given x, y, z and + ve numbers, then value of

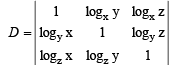
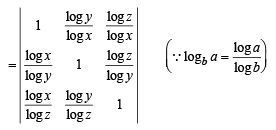
Taking 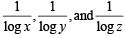  common from R₁, R₂ and R₃ respectively 

True / False

Q. 1. The determinants 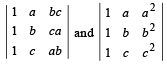are not identically equal.         (1983 - 1 Mark)

Ans. F

Solutions. 

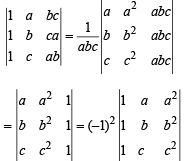
[C₁ ⇔ C₃ and then C₂ ⇔ C₃]
∴ Equal. Hence statement is F.

Q. 2. If 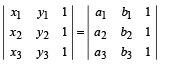 then the two triangles with vertices (x₁ , y₁), (x₂ , y₂), (x₃ , y₃), and (a₁ , b₁), (a₂ , b₂), (a₃ , b₃) must be congruent.    (1985 - 1 Mark)

Ans. F

Solutions. 

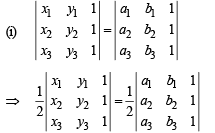
Ar (Δ₁) = Ar (D₂)

Where Δ₁ is the area of triangle with vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃);  and Δ₂ is the area of triangle with ; vertices (a₁, b₁), (a₂, b₂) and (a₃, b₃). But two D’s of same area may not be congruent.

∴ Given statement is false.