JEE Advanced (Matrix Match): Differential Equations | Chapter-wise Tests for JEE Main & Advanced PDF Download

Match the Following

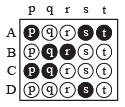
Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in ColumnII. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :

If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q. 1. Match the statements/expressions in Column I with the open intervals in Column II.

Column I                                                                                  Column II

(A) Interval contained in the domain of definition of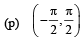                
non-zero solutions of the differential equation
(x – 3)2 + y' + y = 0

(B) Interval containing the value of the integral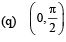                    

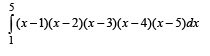
(C) Interval in which at least one of the points of local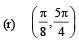          
maximum of
cos²x + sin x lies

(D) Interval in which tan–1 (sin x + cos x) is increasing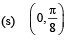         
                                                                                                (t) ( – π,π)

Ans.  (A) → p,q,r,s,t; (B) → p,t; (C) → p,q,r,t; (D) → s

Solution. 

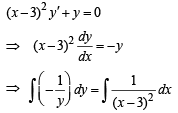
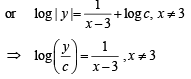
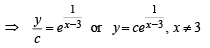
∴ The solution set is (- ∞, ∞)- {3}

The interval 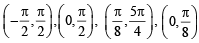 and (–π, π) contained in the domain

∴ (A) → p, q,r , s,t

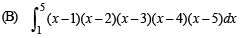
Let ( x - 3) = t ⇒ dx = dt

Also when x ⇒ 1,t → -2

and when x → 5,t → 2

∴ Integral becomes

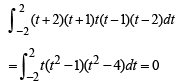
as integrand is an odd function.

O is contained by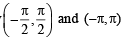 

∴ (B) → p,t.

(C) Let f ( x) = cos² x+ sinx

⇒ f '( x) = -2 sin x cos x+ cosx

For critical point f '(x) = 0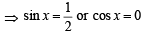 

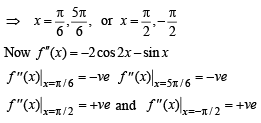
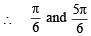 are the points of local maxima.
Clearly all the intervals given in column II except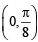  

contain at least one point of local maxima.

∴ (C) → p, q, r,t

(D) Let f ( x) = tan ^-1 (sin x+ cosx)

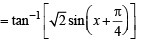
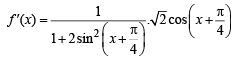
For f (x) to be an increasing function,  f '(x) > 0

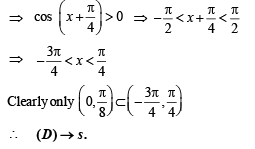
Integer Value Correct Type    

Q. 1. Let y'(x) + y(x) g'(x) = g(x), g'(x),  y(0) = 0, x ∈ R, where f '(x) denotes 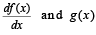is a given non-constantdifferentiable function on R with g(0) = g(2) = 0. Then the value of y(2) is 

Ans. 0

Solution. The given equation is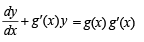  

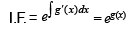
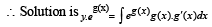
put g (x) = t so that g¢(x) dx = dt

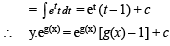
As y (0) = 0 and g (0) = 0

∴ C = 1

∴ y.e^g(x) = e^g(x) [g(x) – 1] + 1
As g (2) = 0, putting x = 2 we get
y(2).e^g(2) = e^g(2) [g(2) – 1] + 1 ⇒ y (2) = 0