JEE Advanced (Matrix Match): Sequences & Series | Chapter-wise Tests for JEE Main & Advanced PDF Download
PASSAGE - 1
Let Vr denote the sum of first r terms of an arithmetic progression (A.P.) whose first term is r and the common difference is (2r – 1).
Let Tr = Vr + 1 – Vr – 2 and Qr = Tr + 1 – Tr for r = 1, 2, ...
1. The sum V1 + V2 + ... + Vn is (2007 -4 marks)
(a)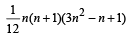
(b) 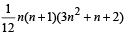
(c) 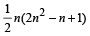
(d) 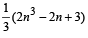
Ans. Sol.
(b) V1 + V2 + .... 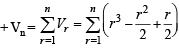
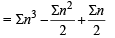
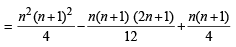
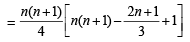
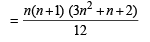
2. Tr is always (2007 -4 marks)
(a) an odd number
(b) an even number
(c) a prime number
(d) a composite number
Ans. Sol.
(d) Tr = Vr +1 -Vr- 2
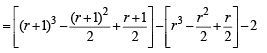
= 3r 2 + 2r+1
Tr = (r + 1) (3r – 1)
For each r, Tr has two different factors other than 1 and itself.
∴ Tr is always a composite number.
3. Which one of the following is a correct statement ? (2007 -4 marks)
(a) Q1, Q2, Q3, ... are in A.P. with common difference 5
(b) Q1, Q2, Q3, ... are in A.P. with common difference 6
(c) Q1, Q2, Q3, ... are in A.P. with common difference 11
(d) Q1= Q2 = Q3 = ....
Ans. Sol.
(b) ∴ Qr +1 - Qr = Tr +2 - Tr +1 - (Tr+1-Tr) = Tr + 2 - 2Tr+1+Tr
= (r+ 3)(3r + 5) - 2(r + 2)(3r + 2)+ (r + 1)(3r -1)
∵Qr + 1 – Qr = 6 (r + 1) + 5 – 6r – 5 = 6 (constant)
∴ ∵1, Q2, Q3, .... are in AP with common difference 6.
PASSAGE -2
Let A1, G1, H1 denote the arithmetic, geometric and harmonic means, respectively, of two distinct positive numbers. For n ≥ 2, Let An – 1 and Hn – 1 have arithmetic, geometric and harmonic means as An, Gn, Hn respectively.
4. Which one of the following statements is correct ? (a) G1 > G2 > G3 > ... (2007 -4 marks) (b) G1 < G2 < G3 < ... (c) G1 = G2 = G3 = ... (d) G1 < G3 < G5 < ... and G2 > G4 > G6 > ....
Ans. Sol.
(c) Given 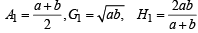
also 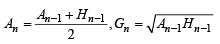
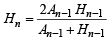
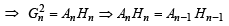
Similarly we can prove
AnHn = An–1Hn–1 = An–2 Hn–2 = .... = A1H1
⇒ AnHn = ab
∴ G12 = G22 = G32 ....= ab
⇒ G1 = G2 = G3 ... 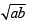
5. Which one of the following statements is correct ? (a) A1 > A2 > A3 > ... (2007 -4 marks) (b) A1 < A2 < A3 < ... (c) A1 > A3 > A5 > ... and A2 < A4 < A6 < ... (d) A1 < A3 < A5 < ... and A2 > A4 > A6 > ...
Ans. Sol.
(a) We have
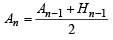
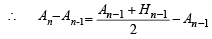
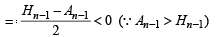
⇒ An < An–1 or An–1 > An ∴ We can conclude that A1 > A2 > A3 > ....
6. Which one of the following statements is correct ? (a) H1 > H2 > H3 > ... (2007 -4 marks) (b) H1 < H2 < H3 < ... (c) H1 > H3 > H5 > ... and H2 < H4 < H6 < ... (d) H1 < H3 < H6 < ... and H2 > H4 > H6 > ...
Ans. Sol.
(b) We have An Hn = ab 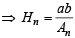
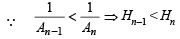 ∴ H1 < H2 < H3 < .......
∴ H1 < H2 < H3 < .......
|
481 docs|964 tests
|
















