JEE Advanced (One or More Correct Option): Differential Equations | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The solution (s) of 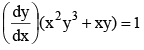 is/are-
is/are-
(a) 1/x = 2 – y2 + Ce-y2/2
(b) the solution of an equation which is reducible to linear equation
(c) 2/x = 1 – y2 + e–y/2
(d) 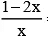 = -y2 + Ce-y2/2
= -y2 + Ce-y2/2
Correct Answer is option (a, b, d)
Given, dy/dx = xy + x2y3
Put,
Integrated Factor =
Q.2. The solution of 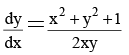 satisfying y(1) = 1 is given by
satisfying y(1) = 1 is given by
(a) a system of hyperbola
(b) a system of circles
(c) y2 = x(1 + x) – 1
(d) (x – 2)2 + (y – 3)2 = 5
Correct Answer is option (a, c)
Rewriting the given equation as

The I.F. of this equation is 1/x, so
⇒ y2 = (x2 - 1) + Cx. Since y(1) = 1 so C = 1,
Hence, y2 = x(1 + x) -1 which represents a system of hyperbola.
Q.3. The differential equation of the curve for which intercept cut by any tangent on y-axis is equal to the length of the sub normal:
(a) is linear
(b) is homogeneous of first degree
(c) has separable variables
(d) is of first order
Correct Answer is option (a, b, d)
Let y = f(x) be the curve
Equation of tangent at (x, y) will be
Y – y = f '(x) (X – x)
Intercept cut by the tangent on y axis will be
y – x f '(x)
So y – xf '(x) =
This is homogeneous equation of first degree & first order Rewriting this equation= 1 which is a linear equation.
Q.4. The differential equation of the curve for which the initial ordinate of any tangent is equal to the corresponding subnormal –
(a) is linear
(b) is homogeneous of first degree
(c) has separable variables
(d) is second degree
Correct Answer is option (a, b)
y = f(x) is a curve
y – y = f ' (x) (X – x) is tangent at (x, y)
f ' (x) = dy/dx X = 0initial ordinate of tangent y – x f '(x).
The subnormal at this point is given by y dy/dx.
y dy/dx = y – x dy/dxdy/dx = y/x + y
This is homogeneous equation
This is linear equation also.
Q.5. The solutions of y = x 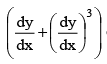 are given by -
are given by -
(a) The constant function y = 0
(b) y = 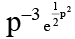 (p + p3)
(p + p3)
(c) y = 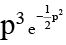 (p + p3)
(p + p3)
(d) 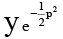 = p–2 + 1
= p–2 + 1
Correct Answer is option (a, b)
Clearly the constant function y = 0 is a solution. Differentiating the give equation w.r.t. x, we get
p = dy/dx = (p + p3) + x
⇒ –p3 = x( 1 + 3p2) dp/dx
⇒ log xp3 = (1/2)p2 + C ⇒ xp3 =
Putting value of x is in the given equation, we have
y =(p + p3)
Q.6. The solution of (dy/dx)2 + 2y cot x dx/dy = y2 is-
(a) y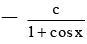 = 0
= 0
(b) y = c/1 - cos x
(c) x = 2 sin–1 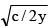
(d) None of these
Correct Answer is option (b, c)
Solving for dy/dx , we obtain
= y (–cot x ± cosec x)
Thus, we have y dy/y = (– cot x + cosec x) dx
⇒ log y = – log sin x + log tan x/2 + log c
⇒
Solving dy/y = – (cot x + cosec x) dx, we get
y = 1/ 1 - cos x
⇒ x = 2 sin–1
Q.7. The solution of y1 (x2y3 + xy) = 1 is
(a) 1/x = 2 –y2 +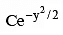
(b) the solution of an equation which is reducible to linear equation
(c) 2/x = 1 - y2 + e-y/2
(d) 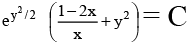
Correct Answer is option (a, b, d)
Re-writing the given equation, we have
dx/dy = x2y3 + xy
⇒ x-2 dx/dy –x–1 y = y3, which is reducible to linear form.
Putting x–1 = u. We have du/dy + yu = –y3
The I.F. of this equation is. So the solution is
Q.8. The solution of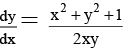 satisfying y (1) = 1 is given by
satisfying y (1) = 1 is given by
(a) a system of hyperbola
(b) a system of circles
(c) y2 = x (1 + x) –1
(d) (x –2)2 + (y –3)2 = 5
Correct Answer is option (a, c)
Re-writing, the given equation asPutting y2 = u, we have
= 1/x + x.
The I.F. of this equation is 1/x, so u.
⇒ y2 = (x2 –1) + Cx.
Since, y(1) = 1 so C = 1,
Hence, y2 = x (1 + x) –1 which represents a system of hyperbola.
Q.9. The solution of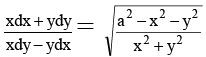 is.
is.
(a) 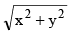 = a (sin (tan–1 y/x) + C
= a (sin (tan–1 y/x) + C
(b) 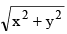 = a ( cos (tan–1 y/x) + C
= a ( cos (tan–1 y/x) + C
(c) 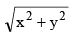 = a (tan (sin–1 y/x) + const)
= a (tan (sin–1 y/x) + const)
(d) y = x tan 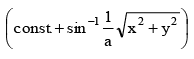
Correct Answer is option (a, d)
Taking, x = r cos θ and y = r sin θ so that x2 + y2 = r2 and y/x = tan θ, we have x dx + y dy = r dr and xdy - ydx = x2 sec2 θ d θ = r2 d θ. The given equation can be transformed into
⇒ C + sin–1 r/a = θ = tan–1 y/x
⇒ y = x tan
ora sin (const + tan–1 y/x)
Q.10. A normal is drawn at a point P(x, y) of a curve. It meets the x- axis at Q. If PQ is of constant length k. Such a curve passing through (0, k) is
(a) a circle with centre (0, 0)
(b) x2 + y2 = k2
(c) (1+ k)x2 + y2 = k2
(d) x2 + (1 + k2) y2 = k2
Correct Answer is option (a, b)
The equation of normal at P(x, y) isY – y = –
So, the coordinates of Q are
Thus PQ2 = (X – x)2 + (0 –y)2 =
To find the equation of the curve we rewrite it as
Integrating, we get...(3)
As the curve passes through (0, k), we get= ± (0) + c ⇒ c = 0
Therefore, (3) can be written as
= ± x ⇒ ± k2 – y2 = x2 or x2 + y2 = k2
|
446 docs|930 tests
|

|
Explore Courses for JEE exam
|

|








 = 1 which is a linear equation.
= 1 which is a linear equation.



 (p + p3)
(p + p3)


 . So the solution is
. So the solution is
 Putting y2 = u, we have
Putting y2 = u, we have = 1/x + x.
= 1/x + x.


 a sin (const + tan–1 y/x)
a sin (const + tan–1 y/x)




 ...(3)
...(3) = ± (0) + c ⇒ c = 0
= ± (0) + c ⇒ c = 0 = ± x ⇒ ± k2 – y2 = x2 or x2 + y2 = k2
= ± x ⇒ ± k2 – y2 = x2 or x2 + y2 = k2















