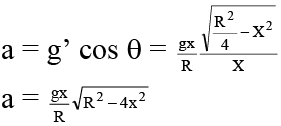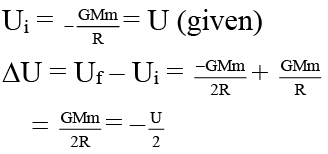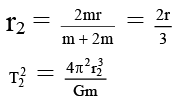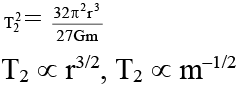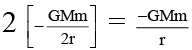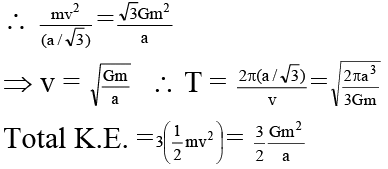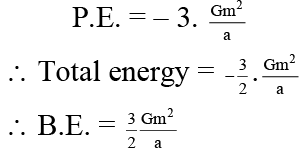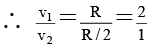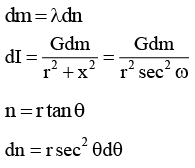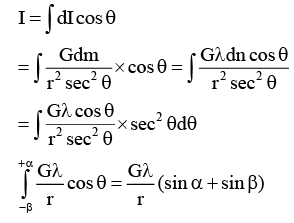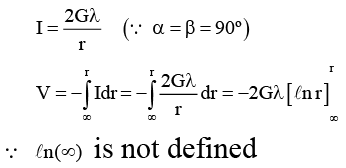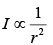JEE Advanced (One or More Correct Option): Gravitation | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth’s centre. The wall of the funnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall and the acceleration of the particle varies with x (distance of the particle from the centre) according to:
(a) 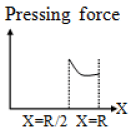
(b) 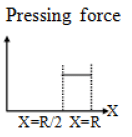
(c) 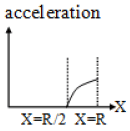
(d) 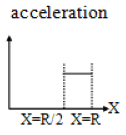
Correct Answer is (b and c)
Net force towards centre of earth
= mg' = mgx/RNormal force N = mg' sin θ
Thus pressing face N = mgx/R R/2xN = mg/2 Constant and independent of X
Tangential force F = ma = mg' cos θ
Curve is parabolic and at X = R/2, a = 0
Q.2. At surface of earth potential energy of a particle is U and potential is V. Change in potential energy and potential at height h = R are suppose DU and DV. Then:
(a) ΔU = - U/2
(b) ΔU = U/2
(c) ΔV = V/2
(d) ΔV = - V/2
Correct Answer is (a and d)
Same is the case with potential.
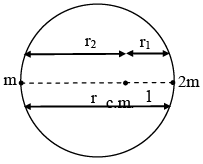
Q.3. A double star in a system of two stars of masses m and 2m, rotating about their centre of mass only under their mutual gravitational attraction. If r is the separation between these two stars then their time period of rotation about their centre of mass will be proportional to
(a) r3/2
(b) r
(c) m1/2
(d) m–1/2
Correct Answer is (a and d)
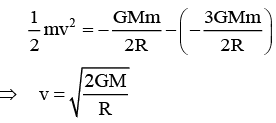
Q.4. Two satellites A and B of equal mass m0, moving in the same circular orbit of radius r around the earth (mass M) but in opposite sense of rotation and therefore on a collision course (see figure), then -
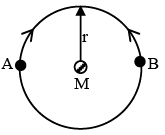
(a) Total mechanical energy of the two satellites plus earth system before collision is –2GMm/r
(b) Total mechanical immediately after completely inelastic collision is–2GMm/r
(c) Subsequent motion of combined satellites mass is along straight line
(d) Subsequent motion of combined satellites mass is along circular orbit of reduced radius.
Correct Answer is (b and c)
(a) T.E. =
(b) T.E. =
(c) Velocity is zero so along straight line towards earth.
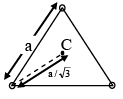
Q.5. Three mass ‘m’ each are kept at corner of a equilateral triangle and are rotating under effect of mutual gravitational force -
(a) Radius of circular path followed by mass is a/2
(b) Velocity of mass is a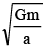
(c) Binding energy of system is 1.5Gm2/a
(d) Time period of mass is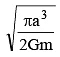
Correct Answer is (b and c)
Distance of any mass from centre = a/√3
Radius of circular path followed = a/√3
Mass is moving in circular path of radius a/√3
Q.6. Two tunnels are dug across the earth as shown in figure. Two particles P1 and P2 are oscillating from one end to the other of tunnel T1 and T2 respectively. At some instant particles are at position shown in figure. Then -
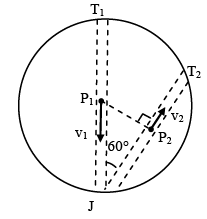
(a) Phase difference between the particle P1 and P2 is 180°.
(b) Phase difference between the particle P1 and P2 is 120°.
(c) Ratio of maximum velocity of particle P1 is to P2 is 2: 1.
(d) Particle P1 and P2 may meet at the junction of the tunnels after some instant.
Correct Answer is (a and c)
At the instant shown, both particle are at their mean position and moving in opposite direction. Phase difference = 180°
As 'ω' is same for both particle
the phase difference will be maintained throughout and they can never meet.
vmax = Aω ⇢ For particle undergoing S.H.M.
(b) the gravitational force at the point B (2, 0, 0) is zero
(c) the gravitational potential is the same at all points of the circle z2 + y2 = 36
Q.7. A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two spheres of equal radii 1 unit, with their centres at (A -2, 0, 0) and B(2, 0, 0) respectively are taken out of the solid leaving behind spherical cavities as shown in the figure. Then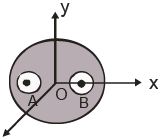 (a) the gravitational force due to this object at the origin is zero
(a) the gravitational force due to this object at the origin is zero
(b) The gravitational force at point B(2,0,0) is zero
(c) the gravitational potential is same at all points of the circle y2 + z2 = 4
(d) The gravitational potential is the same at all the points of circle y2 + z2 =36
Correct Answer is (a, c and d)
The mass of the sphere with cavities is symmetrically situated with respect to the origin. The circle y2 + z2 = 36 , has a radius of 6 units and all points on it are at a distance of 6 from the centre of sphere where the whole mass of the sphere is supposed to be concentrated. The circle is outside the sphere. Similar is the case with circle y2 + z2 = 4 .
Q.8. A particle is dropped from a height equal to the radius of the earth above the tunnel dug through the earth as shown in the figure.
R : Radius of earth.
M : Mass of earth.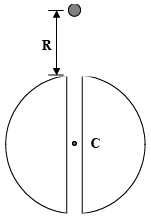
(a) Particle will oscillate through the earth to a height R on both sides
(b) Particle will execute simple harmonic motion
(c) Motion of the particle is periodic
(d) Particle passes the centre of earth with a speed = 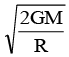
Correct Answer is (a, c and d)
From COE (a) is correct.
The force outside the earth varies as Inverse Square of the distance.
∴ Motion is not simple harmonic. However, from symmetry of motion, the motion will be periodic.
∴ (c) is correct.
From COE
(a), (c) and (d) are correct.
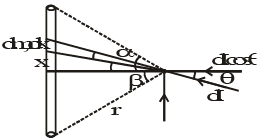
Q.9. The linear mass density of a uniform rod is l then which is correct in the given options?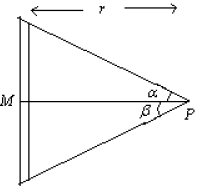 (a) if α = β then Iy = 0 (Iy ⇢ gravitational field in y direction)
(a) if α = β then Iy = 0 (Iy ⇢ gravitational field in y direction)
(b) Ix = 2Gλ/r if length of the rod is infinite
(c) Gravitational potential is not defined at P if length of rod is infinite
(d) If α = β then Ix = 0, Iy = 0
Correct Answer is (a, b and c)
Net intensity of gravitational field
For infinite rod
So, v is not defied here.
Q.10. The magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform, sphere of radius R and mass M are F1 and F2 respectively. then:
(a) 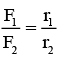 if r1 < R and r2 < R
if r1 < R and r2 < R
(b) 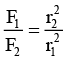 if r1 > R and r2 > R
if r1 > R and r2 > R
(c) 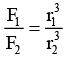 if r1 < R and r2 < R
if r1 < R and r2 < R
(d) 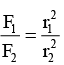 if r1 < R and r2 < R
if r1 < R and r2 < R
Correct Answer is (a and b)
Gravitational field intensity F = GMr/R3Inside the sphere (F1 ∝ r1, F2 ∝ r2)
of r1 < R & r2 < R
Gravitational field intensity
if r1 > R and r2 > R
|
446 docs|929 tests
|