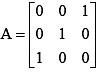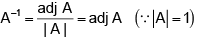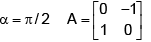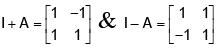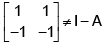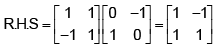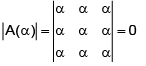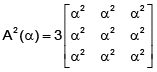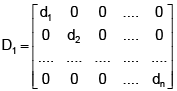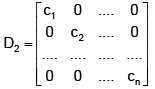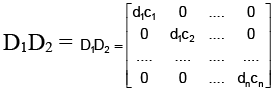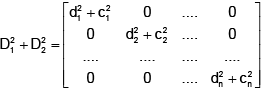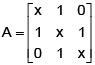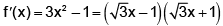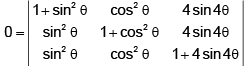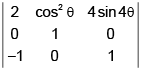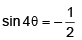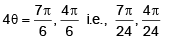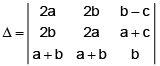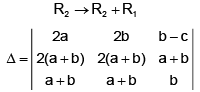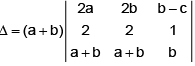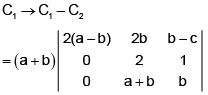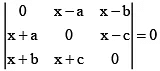JEE Advanced (One or More Correct Option): Matrices & Determinants | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If 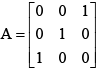, then
(a) Adj A is a zero matrix
(b)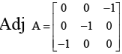
(c) A^–1 =A
(d) A² =I

Correct Answer is options (b, c)
(A) is obviously false and since most of the elements in A are 0, the adjoint can be easily found.
We note that adj
⇒ Choice (B) is correct.
Now
⇒ Choice (C) is also true.
If A² =I then A = A^-1= Adj A which is not true.
⇒ Choice (D) is not true.

Q.2. If 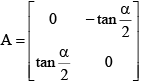 and I is identity matrix of order 2 then
(a)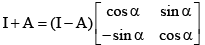
(b)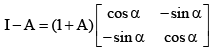
(c)
(d) (A) and (B) are not true

Correct Answer is options (c, d)
If

(A) ⇒ R.H.S. =
⇒ (A) is false
Similarly (B) is incorrect
(C)
= I + A = L.H.S.
If choice (C) is coming out to be true as a special case then only one choice is true which is (D). Since more than one answer should be correct (C) should also be true. We can prove (C) in general.

Q.3. If 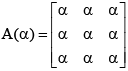, α ≠ 0, then-
(a) 2A(1) = A² (1)
(b) A³ (1) = 9A(1)
(c) (adj.A) does not exist
(d) A ^–1 does not exist.

Correct Answer is options (b, d)

∴ A does not exist.
Now
A² (a) = 3A(α²) ⇒ A² (1) = 3A(1)
⇒ A³ (1) = 3A² (1)
⇒ A³ (1) = 9A(1)

Q.4. If D₁ and D₂ are two diagonal matrices, both of order 3, then -
(a) D₁D₂ is a diagonal matrix
(b) D₁D₂ = D₂D₁ 
(c) D₁² +D₂² is a diagonal matrix
(d) None of these

Correct Answer is options (a, b, c)



= A diagonal matrix
D₁D₂ = D₂D₁

A diagonal matrix

Q.5. Let A =a_ij be a matrix of order 3 where  then which of the following hold(s) good:
(a) for x = 2, A is a diagonal matrix
(b) A is a symmetric matrix
(c) for x = 2, det A has the value equal to 6
(d) Let f(x) = det A, then the function f(x) has both the maxima and minima

Correct Answer is options b, d)

|A| = x³ -  x - 1
If f (x) = x³ -  x - 1

So, x = 1/√3 point of minima and -1/√3 is maxima.

Q.6. System of equation x + 3y + 2z = 6, x + λy + 2z = 7 and x + 3y + 2z = μ has
(a) unique solution if λ = 2, μ ≠ 6
(b) infinitely many solution if  l = 4, μ = 5
(c) no solution if λ = 5, μ = 7
(d) no solution if λ = 3, μ = 5

Correct Answer is options (b, c, d)
x + 3y + 2z = 6 ..................... (i)
x + λy + 2z = 7 ..................... (ii)
x + 3y + 2z = μ ..................... (iii)
(A) If λ= 2, then D = 0, therefore unique solution is not possible
(B) If λ= 4, μ = 6
x + 3y= 6 - 2z
x + 4y= 7 - 2z
∴ y = 1 and x = 3 - 2z
Substituting in equation (iii)
3 – 2z + 3 + 2z = 6 is satisfied
∴ Infinite solutions
(C) λ = 5, μ = 7
Consider equation (ii) and (iii)
x + 5y= 7 - 2z
x + 3y= 7 - 2z
∴ y = 0 x = 7 - 2z are solution
Sub. in (i)
7 – 2z + 2z= 6 does not satisfy
∴ No solution
(D) If λ = 3, μ = 5
Then equation (i) and (ii) have no solution
∴ No solution

Q.7. The values of q lying between θ = 0 & θ = π / 2 & satisfying the equation 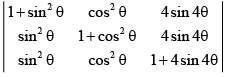 = are –
(a) 7π /24
(b) 5π /24
(c) 11π /24
(d) π /24

Correct Answer is options (a, c)

=
=
= 2 + 4sinθ
∴
∴

Q.8. The determinant 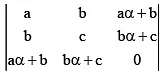 is equal to zero, if
(a) a, b, c are in A.P.
(b) a, b, c are in G. P.
(c) a, b, c are in H.P.
(d) (x – (A)) is a factor of ax² + 2bx+ c

Correct Answer is options (b, d)
Operating R₃ - {αR₁ + R₂} and expanding, we shall easily get

Hence D is zero if ac – b² = 0
or aα² + 2ba + c = 0, i.e., a, b, c are in G.P. or x - α is a factor 2 ax² + 2bx + c.

Q.9. 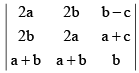 is divisible by
(a) ( a – b )
(b) ( a - b )²
(c) a +b
(d) ( a + b+ c )

Correct Answer is options (a, b, c)




= (a + b)2(a - b)(2b - a - b) = -2(a + b)(a - b)²

Q.10. If a, b, c are positive and distinct then which of the following cannot be roots of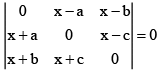
(a) a
(b) 0
(c) b
(d) c

Correct Answer is options (a, c, d)

(x + a)(x - b)(x + c) + (x + b)(x - a)(x - c) = 0
((x² + ac) + x(a + c))(x - b) + ((x² + ac) - (a + c)x)(x + b) = 0
2(x² + ac)x - 2bx(a + c) = 0
x =0 or x² + ac - b(a + c) = 0