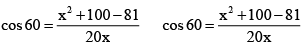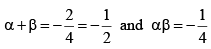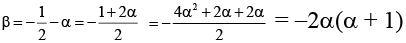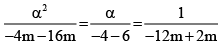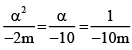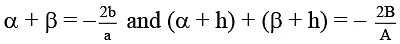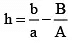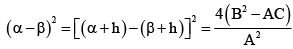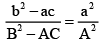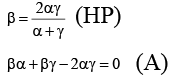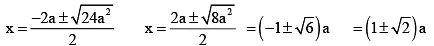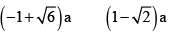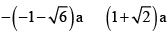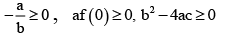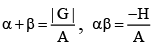JEE Advanced (One or More Correct Option): Quadratic Equation & Inequalities | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. In a triangle the length of two larger sides are 10 and 9 respectively. If the angles are A.P, The length of third side can be.
(a) 5 - √6
(b) 5 + √6
(c) 6 - √5
(d) 6 + √5
Correct Answer is options (a, b)
A,B,C are in A.P LB = 60
x2 - 10x + 19 = 0
x = 5 ± √6
Q.2. If a is a root of the equation 2x(2x + 1) = 1, then the other root is
(a) 3α3 + 4α
(b) 4α3 - 3α
(c) –2α(α + 1)
(d) None of these
Correct Answer is options (b, c)
Let α, β be the roots of
4x2 + 2x - 1 = 0
∴
Also 4α2 + 2α - 1 = 0
Now
and β = -2α2 -2α = α(-2(A) -2α = 4α3 - 3α.
Q.3. The value of m so that the equations 3x2 - 2mx - 4 = 0 and x(x - 4m) + 2 = 0 may have a common roots is
(a) 1 / √2
(b) -1 / √2
(c) 1 / 2
(d) -1 / 2
Correct Answer is options (a, b)
Let α be the common root
Then 3α2 - 2mα - 4 = 0 and α2 - 4mα + 2 = 0
By cross-multiplication, we get
⇒
⇒; or 2m2 = 1;
∴ m = ± 1/√2
Q.4. If the equation x2 - ax + b = 0 and x2 + bx - a = 0 have a common root, then
(a) a =b
(b) a + b= 0
(c) a + b= 1
(d) a - b= 1
Correct Answer is options (b, c)
If α be the common root, then
α2 - aα + b = 0 and α2 + bα - a = 0
Subtracting, α ( b + a ) - ( a + b )
Or ( a + b) (α -1) = 0
∴ α + b =0 or a =1
When α= 1, then from any a - b = 1
Q.5. If α, β are the roots of the equation ax2 + 2bx + c = 0 and α + h, β + h are the roots of the equation Ax2 + 2Bx + C = 0, then
(a) 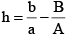
(b) 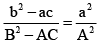
(c) 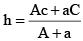
(d) 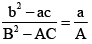
Correct Answer is options (a, b)
We have
⇒⇒
Also
And
Thus,⇒
Q.6. If the a, b, g are the roots of the equation x3 + bx2 + 3x - 1 = 0 ( α ≤ β ≤ γ , α, β, γ are in H.P.) then
(a) One of the roots must be 1
(b) One root is smaller than 1, other is greater than 1
(c) b ∈ [-3, ∞]
(d) All the roots must be equal
Correct Answer is options (a, d)
x2 + bx2 + 3x - 1 = 0
α + β + γ = -b ...(1)
αβ + βγ + γα = -b ...(2)
αβγ = 1 ...(3)
From (A) and (2), γα = 1
From (3), β = 1 and α = γ = β = 1.
Q.7. If 5x2 + 2x + 11 ≡ A(x – (A)2 + B(x – (B)2 where A, B, a, b are integer constants, then
(a) A = 3, B = 1
(b) A = 2, B = 3
(c) A = 3, B = 2
(d) A = 4, B = 1
Correct Answer is options (b, c)
On comparing coefficients, we get
A + B = 5, 2aA – 2bB = 2,
Aa2 + Bb2 + Bb2 = 11
Choice (A) is clearly ruled out since A + B = 5.
For choice (B) equations are 2a + 3b = -1, 2a2 + 3b2 = 11
⇒ a = 8/5, a = -2
For a = -2, b = 1 ⇒ (B) is correct.
Similarly for choice (C), a = 1, b = -2. For choice (D) the equations become
4a + b = -1, 4a2 + b2 = 11
⇒ 10a2 + 4a – 5 = 0 which does not have integer roots. Choice (D) is not possible.
Q.8. If a < 0 then the value (s) of x satisfying x2 - 2a | x - a | -3a2 = 0
(a) 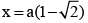
(b) 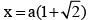
(c) 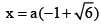
(d) 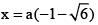
Correct Answer is options (a, c)
x2 + 2a x - a ) - 3a2 = 0
x2 + 2ax - 5a2 = 0
x2 - 2ax - a2 = 0
Q.9. If b2 ≥ 4ac for the equation ax4 + bx2 + c = 0 then all the roots of the equation will be real if
(a) b > 0, a < 0, c > 0
(b) b < 0, a > 0, c > 0
(c) b > 0,a > 0, c > 0
(d) b > 0, a < 0, c < 0
Correct Answer is options (b, d)
Put x2 = y. The given equation becomes
f(y) ≡ ay2 + by + c = 0 (1)
The given equation will have four real roots if (1) has two non-negative roots.
This can happen if
⇒ -ab ≡ 0, ac ≡ 0 [∴ b2 - 4ac ≡ 0 is given]
Thus a and b must have opposite sign whereas a, -b and c must have the same sign.
⇒ a > 0, b < 0, c > 0 or a < 0, b > 0, c < 0.
Q.10. Let A, G and H are the AM, GM and HM respectively of two unequal positive integers. Then the equation Ax2 – |G|x – H = 0 has
(a) At least one root which is an integer
(b) Exactly one positive root
(c) At least one root which is a negative fraction
(d) Both roots as fraction
Correct Answer is options (b, c)
Let α , β be the roots.
As A > |G| > H,
α + β = Positive fraction …(1)
and αβ = negative fraction …(2)
Also AH =| G |2 , D =| G |2 +4AH > 0 Þ roots are real and unequal.
From (2), at least one root is a fraction and of the two roots one root is positive while the other is negative. Also, (1) ⇒ the positive
|
481 docs|964 tests
|