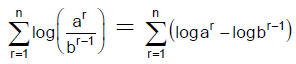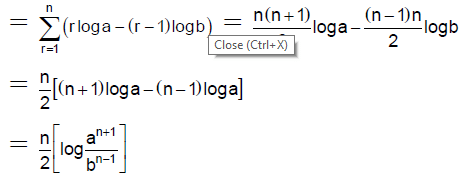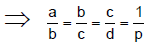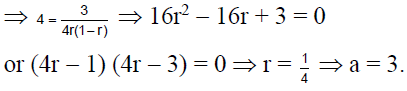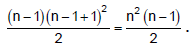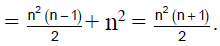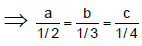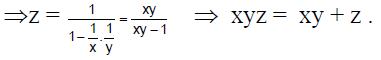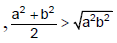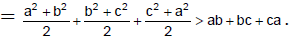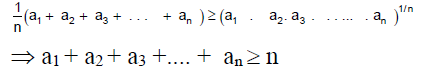JEE Advanced (Single Correct Type): Sequences & Series | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If a, 4, b are in Arithmetic Progression; a, 2, b are in Geometric Progression; then a, 1, b are in
(a) A.P
(b) G.P
(c) H.P
(d) None of these

Correct Answer is option (c)
Given that a, 4, b are in A.P
Hence, 4-a = b-4
a+b = 8 …(1)
Also, given that a, 2, b are in G.P.
Hence, 2/a = b/2
So, ab = 4…(2)
If a, 1, b are in H.P, then 1 = 2(ab)/(a+b) ..(3)
Now substitute (1) and (2) in (3)
1 = 2(4) /(8)
1 = 8/8
1=1.
Therefore, a, 1, b are in H.P.

Q.2. If 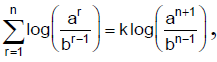 then k is equal to
(a) n + 1
(b) n
(c) n/2
(d)

Correct Answer is option (c)
We have

Q.3. If “a” is the first term and “r” is the common ratio, then the nth term of a G.P is:
(a) arⁿ
(b) ar^n-1
(c) (ar)^n-1
(d) None of these

Correct Answer is option (b)
If “a” is the first term and “r” is the common ratio, the terms of infinite G.P are written as a, ar, ar2, ar3, ar4, …arn-1.
Hence, the nth term of a G.P is arn-1.
Therefore, option (b) is the correct answer.

Q.4. If a, b , c, d and p are distinct real numbers such that (a² + b² + c²)p² – 2(ab + bc + cd ) p + (b² + c² + d²) ≤ 0 , then a, b, c, d are in
(a) A.P.
(b) G.P.
(c) H. P.
(d) none of these

Correct Answer is option (b)

The given inequality can be re-written as

 (ap – b)² + (bp - c)² +( cp - d)² ≤ 0

⇒ ap – b = bp – c = cp - d = 0

⇒ a, b, c, d are in G. P.

Q.5. If a, b, c are in arithmetic progression, then
(a) b = a+c
(b) 2b = a+c
(c) b² = a+c
(d) 2b² = a+c

Correct Answer is option (b)
Given that a, b, c are in arithmetic progression.
So, the common difference is b-a = c-b
Rearranging the same terms, we get
b+b = c+a
2b = a+c.
Hence, if a, b, c are in A.P, then 2b = a+c.

Q.6. In an infinite geometric series, with first term a and common ratio r, the second term is 3/4 and its sum is 4. Then
(a) a = 7/4, b = 3/7
(b) a=3/2, r = 1/2
(c) a = 2, r = 3/2
(d) a = 3, r = 1/4

Correct Answer is option (d)
Here, the sum of the series  and the second term = 3/4 = ar

Q.7. The sum of arithmetic progression 2, 5, 8, …, up to 50 terms is
(a) 3775
(b) 3557
(c) 3757
(d) 3575

Correct Answer is option (a)
Given A.P. = 2, 5, 8, …
We know that the sum of n terms of an A.P is S_n = (n/2)[2a+(n-1)d]
Here, a = 2, d = 3 and n=50.
Now, substitute the values in the formula, we get
S50 = (50/2)[2(2)+(50-1)(3)]
S50 = 25[4+(49)(3)]
S50 = 25[4+147]
S50 = 25(151)
S50 = 3775.
Hence, the sum of A.P 2, 5, 8, …up to 50 terms is 3775.

Q.8. The sum of the first n terms of the series

when n is even. When n is odd, the sum is
(a)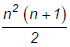
(b)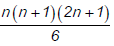
(c)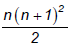
(d)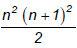

Correct Answer is option (a)
If n is odd, n-1 is even. Sum of (n-1) terms will be

The nth term will be n². Hence the required sum

Q.9. The 3rd term of G.P is 4. Then the product of the first 5 terms is:
(a) 4³ 
(b) 4⁴
(c) 4⁵
(d) None of these

Correct Answer is option (c)

We know that the terms of infinite G.P are written as a, ar, ar², ar³, ar⁴, …ar^n-1.
Hence, the 3rd term, (i.e) ar²= 4
Thus, the product of the first 5 terms = (a)(ar)(ar²)(ar³)(ar⁴)
= a⁵r¹⁰ 
= (ar²)⁵
Now, substitute ar² = 4 in the above form, we get
Product of the first 5 terms = (4)⁵ = 4⁵.
Hence, option (c) 4⁵ is the correct answer.

Q.10. Let α, β be the roots of x² - x + p = 0 and γ, δ be the roots of x² - 4x + q = 0. If α, β, γ, δ are in G.P., then the integral values of p and q respectively are
(a) -2, - 32
(b) -2, 3
(c) -6, 3
(d) -6, - 32

Correct Answer is option (a)

Here α + β = 1, αβ = p, γ + δ = 4, δγ = q.

Since, α, β, γ, δ are in G.P., with common ratio (say) r,
α (1 + r) = 1, α (r² + r³) = 4
⇒ r² = 4 ⇒ r = ± 2.
⇒ α = -1 for r = -2 (for integral values of p, q) and p =
αβ = α²r = -2
q= γδ = α²r⁵ = -32.

Q.11. Which of the following is an example of a geometric sequence?
(a) 1, 2, 3, 4
(b) 1, 2, 4, 8
(c) 3, 5, 7, 9
(d) 9, 20, 21, 28

Correct Answer is option (b)
Among the options given, option (b) 1, 2, 4, 8 is an example of a geometric sequence.
We know that in a geometric sequence each term is found by multiplying the previous term by a constant.
In option (b) 1, 2, 4, 8, each term is found by multiplying 2 to the previous term. Here, the common ratio is 2.

Q.12. If p, q, r are in A.P. , then p^th, q^th and r^th terms of any G.P. are in
(a) A.P.
(b) G. P.
(c) H. P.
(d) A.G.P.

Correct Answer is option (b)

Let the first term of a G.P. be A and common ratio be R. Then p^th, q^th and r^th terms are AR^p-1, AR^q-1 and AR^r-1.
Obviously
AR^p-1x AR^r-1 = A²R^p+r—2 = (AR^q-1)², as p + r = 2q. Hence terms are in G.P.

Q.13. The next term of the given sequence 1, 5, 14, 30, 55, … is
(a) 80
(b) 90
(c) 91
(d) 96

Correct Answer is option (c)
The next term in the sequence 1, 5, 14, 30, 55, … is 91.
Ist term = 1² = 1
2nd term = 1²+2² = 1+4 = 5
3rd term = 1²+2²+3² = 1+4+9 = 14
4th term = 1²+2²+3²+4² = 1+4+9+16 = 30
5th term = 1²+2²+3²+4²+5² = 1+4+9+16+25 = 55
6th term = 1²+2²+3²+4²+5²+6² = 1+4+9+16+25+36 = 91.
Thus, option (c) is the correct answer.

Q.14. If 4a² + 9b² + 16c² = 2(3ab + 6bc + 4ca), where a, b, c are non-zero numbers, then a, b, c are in
(a) A.P.
(b) G.P.
(c) H.P
(d) none of these

Correct Answer is option (c)

The given equation 4a² + 9b² + 16c² = 2(3ab + 6bc + 4ca) = (2a – 3b)² + (3b – 4c)² + (4c – 2a)² = 0 ⇒ 2a = 3b = 4c

⇒ a, b, c are in H.P.

Q.15. If the nth term of an arithmetic progression is 3n-4, then the 10th term of an A.P is
(a) 10
(b) 12
(c) 22
(d) 26

Correct Answer is option (d)

Given that the nth term of A.P = 3n-4.

To find the 10th term of A.P, substitute n = 10

Therefore, 10th term of A.P = 3(10) -4 = 30-4 = 26.

Q.16. For 0 < θ <π/2, if 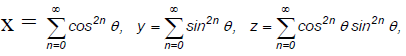 then
(a) xyz = xz + y
(b) xyz = xy +z
(c) xyz = yz +x
(d) none of these

Correct Answer is option (b)
Here

Q.17.  3, 5, 7, 9 is an example of
(a) Arithmetic sequence
(b) Geometric sequence
(c) Harmonic sequence
(d) Fibonacci sequence

Correct Answer is option (a)
3, 5, 7, 9 is an example of an arithmetic sequence. In this sequence 3, 5, 7, 9, the difference between each term is 2.
(i.e) 5-3 = 2, 7-5 = 2, 9-7 = 2.
Hence 3, 5, 7, 9 is an arithmetic sequence.

Q.18. If a, b and c are distinct positive real numbers and a2 +b2+c2 =1, then ab + bc +ca is
(a) less than 1
(b) equal to 1
(c) greater than 1
(d) any real number.

Correct Answer is option (a)
Since a and b are unequal

(A.M. > G.M. for unequal numbers)

⇒ a² +b²> 2ab.
Similarly b² +c² > 2bc and c² +a² > 2ca.
Hence 2(a² +b² +c² ) > 2(ab + bc +ca)

⇒ ab +bc +ca < 1.
Hence (A) is the correct answer.

Alternative solution:
It is given that 1 = a² + b² + c²

Q.19. The first term of a G.P is 1. The sum of the 3rd and 5th terms is 90. Then the common ratio is:
(a) 1
(b) 2
(c) 3
(d) 4

Correct Answer is option (a)

Given that first term of G.P, a = 1.

The sum of the 3rd and 5th term = 90

(i.e) ar²+ar⁴ = 90

Substitute a = 1,

⇒ r²+r⁴ = 90

⇒ r⁴ + r² – 90 = 0

⇒ r⁴ + 10r² – 9r² – 90 = 0

Now, factorize the above equation,

⇒ r² (r²+10) – 9 (r²+10) = 0

⇒ (r²-9)(r²+10) = 0

⇒ r² = 9 or r² = -10

Here, r²= -10 is not possible, as the square of a number cannot be negative.

So, r² = 9

r = 3 or r= -3

Therefore, option (c) 3 is the correct answer.

Q.20. If the product of n positive numbers is unity , then their sum is

(a) a positive integer
(b) divisible by n
(c) equal to n +1/n
(d) never less than n.

Correct Answer is option (d)

Let the numbers be a₁; a₂; a₃ ;. . . ; an . Then a₁. a₂. a₃ . . . .a_n =1. Using A.M. ≥ G.M , we get