JEE Advanced (Subjective Type Questions): Applications of Derivatives - 2 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.22. The curve y = ax³ + bx² + cx + 5, touches the x-axis at P(–2, 0) and cuts the y axis at a point Q, where its gradient is 3. Find a, b, c.           (1994 - 5 Marks)

Ans.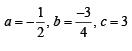 

Solution. Given that y = ax³ + bx² + cx + 5 touches the x-axis at P (–2, 0)

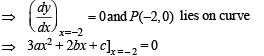
an d – 8a + 4 b – 2c + 5 = 0 ...(2)

[∴ (– 2, 0) lies on curve]

Also the curve cuts the y-axis at Q

∴ For x = 0, y = 5 ∴ Q (0, 5) At Q gradient of the curve is 3

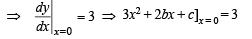
⇒ c = 3 ...(3)

Solving (1), (2) and (3), we get a = – 1/2, b = – 3/4 and c = 3.

Q.23. The circle x² + y² = 1 cuts the x-axis at P and Q. Another circle with centre at Q and variable radius intersects the first circle at R above the x-axis and the line segment PQ at S.

Find the maximum area of the triangle QSR.            (1994 - 5 Marks)

Ans.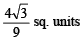 

Solution. The given circle is x² + y² = 1 ...(1)

which intersect x-axis at P (– 1, 0) and Q (1, 0).

Let radius of circle with centre at Q (1, 0) be r, where r is variable.

Then equation of this circle is,

(x – 1)² + y² = r²        ...(2)

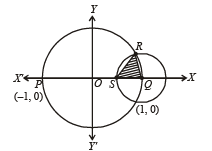
Subtracting (1) from (2) we get

(x – 1)² – x² = (r² – 1)

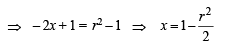
Substituting this value of x in (2), we get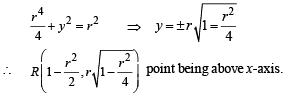


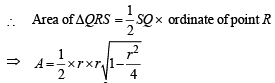
A will be  max. if A² is max.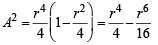

Differentiating A² w.r. to r, we get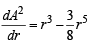 

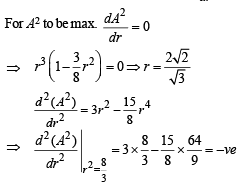
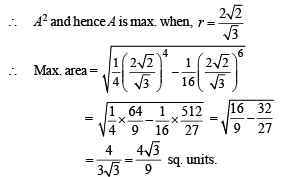
Q.24. Let (h, k) be a fixed point, where h > 0, k > 0. A straight line passing through this point cuts the positive direction of the coordinate axes at the points P and Q. Find the minimum area of the triangle OPQ, O being the origin.              (1995 - 5 Marks)

Ans. 2 kh

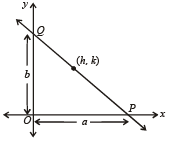
Solution. Let the given line be 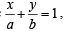  so that it makes an intercept of a units on x-axis and b units on y-axis. As it passes through the fixed point (h, k), therefore we must have

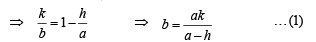
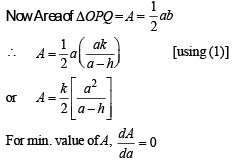
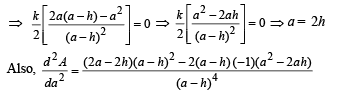
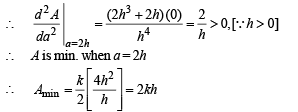
Q.25. A curve y = f(x) passes through the point P(1,1). The normal to the curve at P is a(y – 1) + (x – 1) = 0. If the slope of the tangent at any point on the curve is proportional to the ordinate of the point, determine the equation of the curve. Also obtain the area bounded by the y-axis, the curve and the normal to the curve at P.             (1996 - 5 Marks)

Ans. y = e^{a (x -1)} ; 1 sq. unit

Solution. The normal to the curve at P is a (y – 1) + (x – 1) = 0

First we consider the case when a ≠ 0

Slope of normal at P (1 , 1) is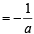 

⇒ Slope of the tangent at (1, 1) is = a

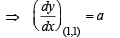              … (1)

But we are given that

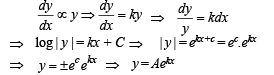
Where A is constant. As the curve passes through (1, 1)

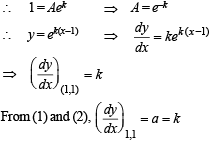
∴ y = e^{a(x – 1)} which is the required curve.
Now the area bounded by the curve, y-axis and normal to curve at (1, 1) is as shown the shaded region in the fig.

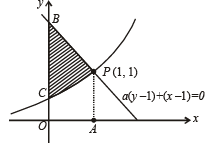
∴ Req. area = ar (PBC) = ar (OAPBCO) – ar (OAPCO)

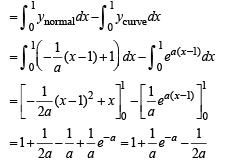
Now we consider the case when a = 0. Then normal at (1, 1) becomes x – 1 = 0 which is parallel to y-axis, therefore tangent at (1, 1) should be parallel to x-axis. Thus

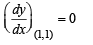                       … (3)

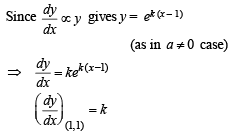
From (3) and (4), we get k = 0 and required curve becomes y = 1

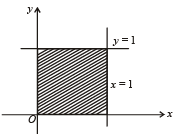
In this case the required area = shaded area in fig. = 1 sq. unit.

Q.26. Determine the points of maxima and minima of the function 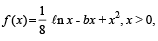 where b > 0 is a constant.           (1996 - 5 Marks)

Ans.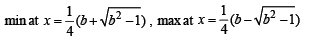 

Solution.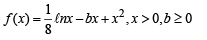 

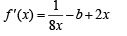                   … (1)

f '(x) = 0 ⇒ 16x² - 8bx + 1=0 (for max. or min.) 

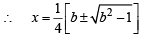        … (2)

Above will give real values of x if b² – 1 > 0 i.e. b > 1 or b < -1 . But b is given to be +ve. Hence we choose b > 1

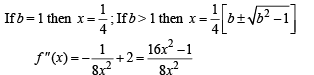
Its sign will depend on Nr, 16x² – 1 as 8x² is +ve. We shall consider its sign for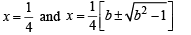 

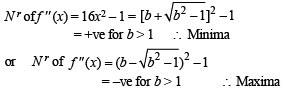
Q.27.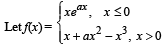 

Where a is a positive constant. Find the interval in which f ' (x) is increasing.                  (1996 - 3 Marks)

Ans.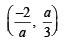 

Solution.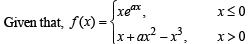 

Differentiating both sides, we have

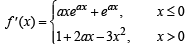
Again differentiating both sides, we have

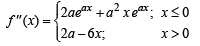
For critical points, we put f ''(x) =0

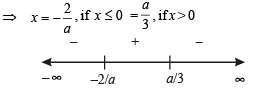
It is clear from number line that

Q.28. Let a + b = 4, where a < 2, and let g(x) be a differentiable function.             (1997 - 5 Marks)

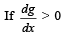for all x, prove that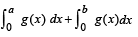 

Solution.

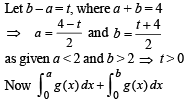
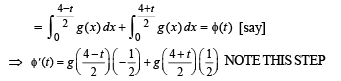
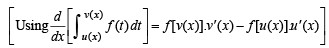
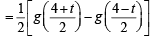
Since g (x) is an increasing function (given)

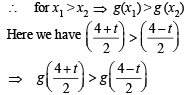
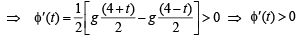
Hence φ (t) increase as t increases.

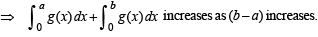
Q.29. Suppose f(x) is a function satisfying the following conditions                       (1998 - 8 Marks)

(a) f(0) = 2, f(1) = 1,
 (b) f has a minimum value at x = 5/2, and
 (c) for all x,

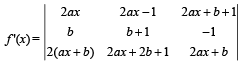
where a, b are some constants. Determine the constants a, b and the function f(x).

Ans.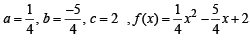 

Solution. Applying R₃ → R₃ - R₁- 2R₂ we get

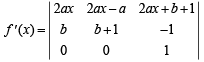
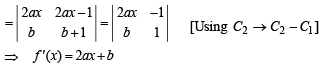
⇒ f '(x) = 2ax+b

Integrating, we get , f (x) = ax2 + bx + C where C is an arbitrary constant. Since f has a maximum at x = 5/2,

f '(5 / 2) = 0 ⇒ 5a +b=0 … (1)

Also f (0) = 2 ⇒ C = 2

and f (1) = 1 ⇒ a + b + c = 1

∴ a + b = – 1 … (2)

Solving (1) and (2) for a, b we get,

a = 1/4, b = – 5/4

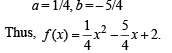
Q. 30. A curve C has the property that if the tangent drawn at any point P on C meets the co-ordinate axes at A and B, then P is the mid-point of AB. The curve passes through the point (1, 1). Determine the equation of the curve.               (1998 - 8 Marks)

Ans. xy = 1

Solution. Equation of the tangent at point (x, y) on the curve is

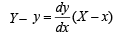
This meets axes in

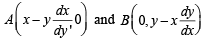
Mid-point of AB is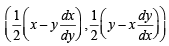 

We are given

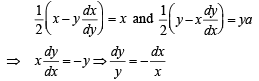
Intergrating both sides,

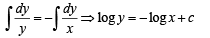
Put x = 1, y = 1,
⇒ log 1 = – log 1 + c  ⇒ c = 0 ⇒ log y + log x = 0
⇒ log yx = 0 ⇒ yx = e⁰ = 1

Which is a rectangular hyperbola.

Q. 31. Suppose p(x) = a⁰ + a₁x + a₂x² +....... + a_nxⁿ. If 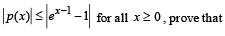 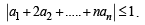            (2000 - 5 Marks)

Solution. Given that,  p (x) = a₀ + a₁ x + a₂ x² + … + a_nxⁿ … (1)

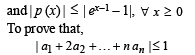
It can be clearly seen that in order to prove the result it is sufficient to prove that | p '(1) | < 1

We know that,

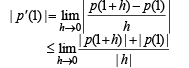
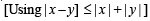
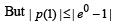   [Using equation (2) for x = 1]

⇒ | p(1) | < 0

But being absolute value, | p(1) | > 0 .
Thus we must have | p(1) | =0

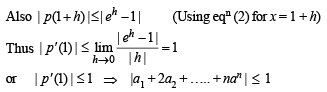
Q. 32. Let - 1 < p < 1. Show that the equation 4x³ - 3x - p = 0 has a unique root in the interval[1/2, 1] and identify it.           (2001 - 5 Marks)

Solution. Given that -1 < p < 1 .
Consider f (x) = 4x³ – 3x – p = 0

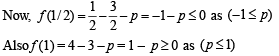
∴  f (x) has at least one real root between [1/2, 1].
Also f '(x) = 12x² - 3>0 on [1/2, 1]
⇒ f is increasing on [1/2, 1]
⇒ f has only one real root between [1/2, 1]

To find the root, we observe f (x) contains 4x³ – 3x which is multipe angle formula of cos 3θ if we put x = cos θ.
∴ Let the req. root be cos θ then,

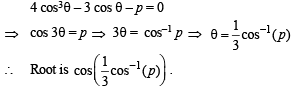
Q. 33. Find a point on the curve x² + 2y² = 6 whose distance from the line x + y = 7, is minimum.             (2003 - 2 Marks)

Ans. (2, 1)

Solution. The given curve is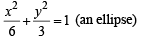 

Any parametric point on it is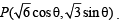 

Its distance from line x + y = 7 is given by 

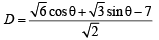
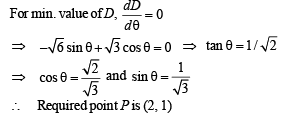
Q. 34. Using the relation 2(1 – cos x) < x², x ≠ 0 or otherwise, prove that sin (tan x) 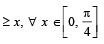            (2003 - 4 Marks)

Solution. Given that 2 (1– cos x) < x², x ≠ 0

To prove sin (tan x) > x, x ∈ [0,π / 4).

Let us consider f (x) = sin (tan x) – x

⇒ f '( x) = cos (tan x) sec² x- 1

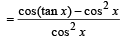
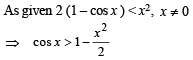
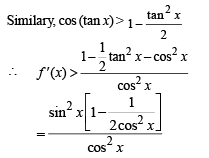
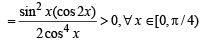
∴ f '(x) > 0 ⇒ f (x) is an increasing function.

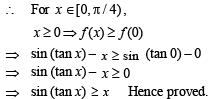
Q. 35. If the function f : [0,4] → R is differentiable then show that             (2003 - 4 Marks)

(i) For a, b ∈ (0,4), (f(4))² – (f(0))² = 8f '(a) f(b)

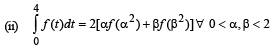
Solution. Given that f is a differentiable function on [0, 4]

∴ It will be continuous on [0, 4]

∴ By Lagrange's mean value theorem, we get

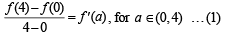
Again since f is continuous on [0, 4] by intermediate mean value theorem, we get

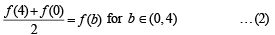
[If f (x) is continuous on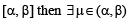 

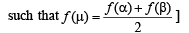
Multiplying (1) and (2) we get

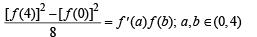
or[f (4)]² – [f (0)]² = 8 f ' (a) f (b) 

Hence Proved.

(ii) To prove

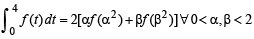
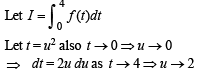
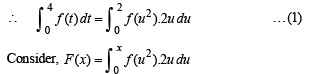
Then clearly F (x) is differentiable and hence continuous on [0, 2]
By LMV theorem, we get some, μ∈ (0, 2)

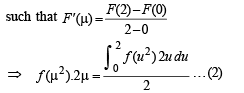
Again by intermediate mean value theorem,

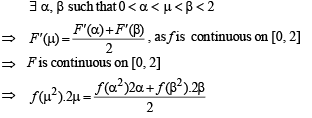
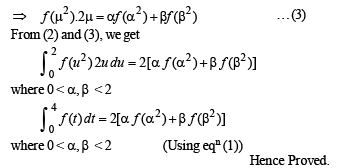
Q. 36. 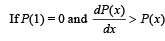for all x > 1 then prove that P(x) > 0 for all x > 1.                 (2003 - 4 Marks)

Solution. We are given that,

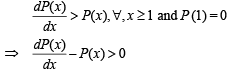
Multiplying by e^–x, we get,

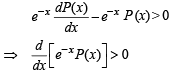
⇒ e^–x P(x) is an increasing function.

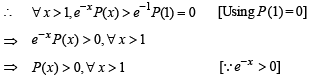
Q. 37. Using Rolle’s theorem, prove that there is at least one root in (45^1/100, 46) of the polynomial          (2004 - 2 Marks)

P(x) = 51x¹⁰¹ – 2323(x)¹⁰⁰ – 45x + 1035.

Solution. We are given,

P(x) = 51x¹⁰¹ – 2323(x)¹⁰⁰ – 45x + 1035.

To show that at least one root of P (x) lies in (45^1/100, 46), using Rolle's theorem, we consider antiderivative of P (x)

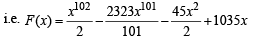
Then being a polynominal function F(x) is continuous and differentiable.

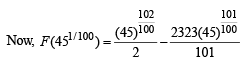
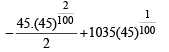
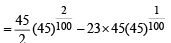
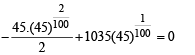
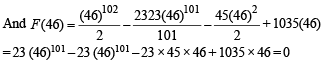
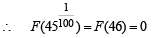
∴ Rolle's theorem is applicable.
Hence, there must exist at least one root of F '(x) = 0

i.e. P (x) = 0 in the interval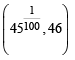 
Q. 38. Prove th at for 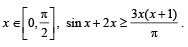 Explain the identity if any used in the proof.           (2004 - 4 Marks)

Solution. Let us consider,

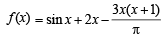
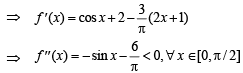
⇒  f '(x) is a decreasing function.   .... (1)

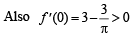            … (2)

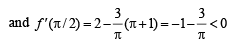           …(3)

Equations (1), (2) and (3) shows that.
⇒ There exists a certain value of x ∈ [0,π / 2] for which f ' (x) = 0 and this point must be a point of maximum for f (x) since the sign of f ' (x) changes from +ve to –ve.

Also we can see that f (0) = 0 and

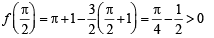
Let x = p be the point at which the max. of f (x) occurs.
There will be only one max. point in [0, π/2]. Since f '(x) = 0 is only once in the interval.
Consider ,  x ∈ [0,p]

⇒ f ' (x) > 0  ⇒ f (x) is an increasing function.

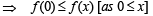
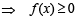             ..... (4)

Also for x ∈[p,π / 2]

⇒ f ' (x) < 0  ⇒ f (x) is decreasing function.

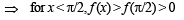              ..... (5)

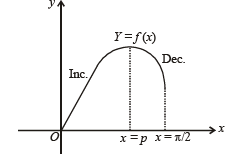
Hence from (4) and (5) we conclude that

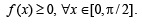
Q. 39. If |f (x₁) – f (x₂)| < (x₁ – x₂)², for all x₁, x₂ ∈ R. Find the equation of tangent to the cuve y = f (x) at the point (1, 2).          (2005 - 2 Marks)

Ans. y = 2

Solution. Given that,  | f (x₁) – f (x₂) | < (x₁ – x₂)², x₁ , x₂ ∈ R

Let x₁ = x + h and x₂ = x then we get

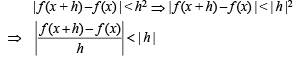
Taking limit as h → 0 on both sides, we get

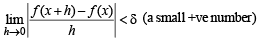
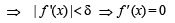
⇒ f (x) is a constant function. Let f (x) = k i.e., y = k

As f (x) passes through (1, 2) ⇒ y = 2

∴ Equation of tangent at (1, 2) is,

y – 2 = 0 (x – 1) i.e. y = 2

Q. 40. If p(x) be a polynomial of degree 3 satisfying p(–1) = 10, p(1) = –6 and p(x) has maxima at x = – 1 and p'(x) has minima at x = 1. Find the distance between the local maxima and local minima of the curve.             (2005 - 4 Marks)

Ans.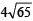 

Solution. Let p (x) = ax³ + bx² + cx + d

p (– 1) = 10

⇒ – a + b – c + d = 10 ...... (i)

p (1) = – 6

⇒ a + b + c + d = – 6 ...... (ii)

p (x) has max. at x = – 1

∴ p' (– 1) = 0

⇒ 3a – 2b + c = 0 ...... (iii)

p' (x) has min. at x = 1

∴ p'' (1) = 0

⇒ 6a + 2b = 0 ...... (iv)

Solving (i), (ii), (iii) and (iv), we get

From (iv), b = – 3a

From (iii), 3a + 6a + c = 0 ⇒ c = – 9a

From (ii), a – 3a – 9a + d = – 6 ⇒ d = 11a – 6

From (i), – a – 3a + 9a + 11a – 6 = 10

⇒ 16a = 16 ⇒ a = 1 ⇒ b = – 3, c = – 9, d = 5

∴ p (x) = x³ – 3x² – 9x + 5

⇒ p' (x) = 3x² – 6x – 9 = 0

⇒ 3 (x + 1) (x – 3) = 0 ⇒ x = – 1 is a point of max. (given) and x = 3 is a point of min.

[∴ max. and min. occur alternatively]

∴ points of local max. is (– 1, 10) and local min. is (3, – 22).

And distance between them is

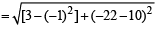
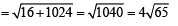
Q. 41. For a twice differentiable function f (x), g(x) is defined as g(x) = (f '(x)² + f"(x)) f(x) on [a, e]. If for a < b < c < d < e, f (a) = 0, f (b) = 2, f (c) = –1, f (d) = 2, f (e) = 0 then find the minimum number of zeros of g(x).           (2006 - 6M)

Ans. 6

Solution.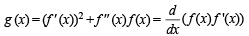 

Let h (x) = f (x) f ' (x)

Then, f (x) = 0 has four roots namely a, a, b, e

where b < a < c and c < b < d.

And f ' (x) = 0 at three points k₁, k₂, k₃

where a < k₁ < α, α < k₂ < β, β < k₃ < e

[∴ Between any two roots of a polyn omial fun ction f (x) = 0 there lies atleast one root of f ' (x) = 0]

∴ There are atleast 7 roots of f (x) . f ' (x) = 0

⇒  There are atleast 6 roots of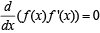 

i.e. of g (x) = 0