JEE Advanced (Subjective Type Questions): Chemical Kinetics & Nuclear Chemistry- 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download
1. Rate of a reaction A + B → products, is given below as a function of different initial concentrations of A and B : (1982 - 4 Marks)
| [A] (mol/l) | [B] (mol/l) | Initial rate (mol/l/min) |
| 0.01 | 0.01 | 0.005 |
| 0.02 | 0.01 | 0.010 |
| 0.01 | 0.02 | 0.005 |
Determine the order of the reaction with respect to A and with respect to B. What is the half-life of A in the reaction?
Solution:
From data (i) and (ii) it is obvious that when the concentration of B is kept constant (0.01 mol litre–1) and the concentration of A is doubled (0.01 to 0.02 mol litre–1), the rate of reaction is also doubled (0.005 to 0.010 mol litre–1 min–1). This shows that the rate of reaction varies directly as the first power of the concentration. Hence the order of reaction with respect to A is 1.
Similarly, from data (i) and (iii) it is obvious that when the concentration of A is kept constant (0.01 mol litre–1) and the concentration of B doubled (0.01 to 0.02 mol litre–1), the rate of reaction remains constant (0.005 mol litre–1 min–1). This shows that the order of reaction with respect to B is zero. Now we know that the rate of reaction, A + B ® Products, is given by
Rate r = k [A]1[B]0 ⇒ r = k [A]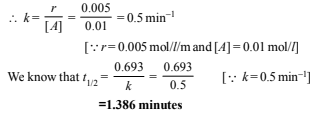
2. Radioactive decay is a first order process. Radioactive carbon in wood sample decays with a half life of 5770 years. What is the rate constant (in years–1) for the decay? What fraction would remain after 11540 years? (1984 - 3 Marks)
Solution: 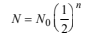
Half life, t1/2 = 5770 years
Let the original sample be 1 gram.
∴ After every 5770 years one-half of radioactive carbon would decay or disintegrate.
Thus, 1 g sample becomes 1⁄2 g after 5770 years and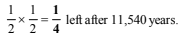
∴ 25% of radioactive carbon remains after 11540 years. Rate constant, k for first order reaction,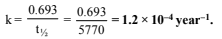
3. While studying the decomposition of gaseous N2O5 it is observed that a plot of logarithm of its partial pressure versus time is linear. What kinetic parameters can be obtained from this observation? (1985 - 2 Marks)
Solution:
Assuming that the decomposition of N2O5 is a first order reaction, then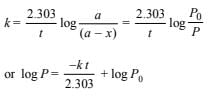
Thus log P vs time graph is linear with slope = -k/2.303 if the given reaction is of first order which is in accordance with the given statement. Thus the reaction obeys first order reaction.
4. 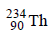 disintegrates to give
disintegrates to give 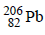 as the final product. How many alpha and beta particles are emitted during this process? (1986 - 2 Marks)
as the final product. How many alpha and beta particles are emitted during this process? (1986 - 2 Marks)
Solution: 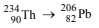
NOTE : For emission of one a-particle, atomic mass decreases by 4 and atomic number by 2. Further for the emission of one b-particle, the atomic mass does not change but the atomic number increases by 1. So we first find the a-particles :
Decrease in atomic mass = 234 – 206 = 28
No. of a-particles emitted = 28/4 = 7
Hence, atomic number should have decrease to
90 – (7 × 2) = 76
Now, atomic number of Pb = 82,
which is more by (82 – 76) = 6
This increase is due to ionisation of β-particles.
Therefore, β-particles emitted = 6.
5. A first order reaction has K = 1.5 × 10–6 per second at 200ºC. If the reaction is allowed to run for 10 hours, what percentage of the initial concentration would have changed in the product? What is the half life of this reaction? (1987 - 5 Marks)
Solution:
For a first order reaction we know that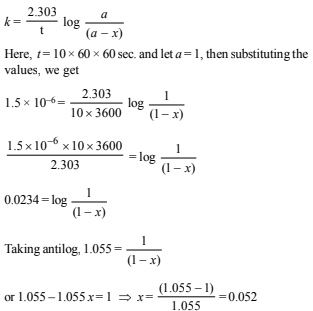
Thus, 5.2% of the initial concentration has changed into product.
Again we know that
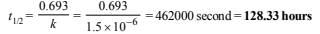
6. A first order reaction is 50% complete in 30 minutes at 27ºC and in 10 minutes at 47ºC. Calculate the reaction rate constant at 27ºC and the energy of activation of the reaction in kJ/mole. (1988 - 3 Marks)
Solution: 
7. An experiment requires minimum beta activity product at the rate of 346 beta particles per minute. The half life period of 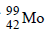 , which is a beta emitter is 66.6 hours. Find the minimum amount of
, which is a beta emitter is 66.6 hours. Find the minimum amount of 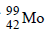 required to carry out the experiment in 6.909 hours. (1989 - 5 Marks)
required to carry out the experiment in 6.909 hours. (1989 - 5 Marks)
Solution:
Minimum number of b-particles required in one minute = 346
No. of b-particles required for carrying out the experiment for 6.909 × 60 minutes = 346 × 6.909 × 60 = 143431
∴ Amount of b-particles required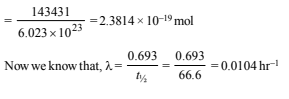

8. In the Arrhenius equation for a certain reaction, the value of A and Ea (activation energy) are 4 × 1013 sec–1 and 98.6 kJ mol–1 respectively. If the reaction is of first order, at what temperature will its half-life period be ten minutes? (1990 - 3 Marks)
Solution:
According to Arrhenius equation
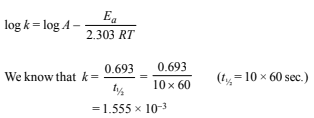
Substituting the various values in the above equation, we get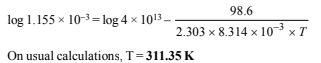
9. The decomposition of N2O5 according to the equation : (1991 - 6 Marks)
2N2O5(g) → 4NO2(g) + O2(g)
is a first order reaction. After 30 min. from the start of the decomposition in a closed vessel, the total pressure developed is found to be 284.5 mm of Hg and on complete decomposition, the total pressure is 584.5 mm of Hg. Calculate the rate constant of the reaction.
Solution:
2N2O5(g) ® 4NO2(g) + O2(g)
2 mol of gaseous nitrogen pentoxide on complete decomposition gives 5 mol of gaseous products.
Therefore, initial pressure of N2O5 = 584.5 × 2/5
= 233.8 mm Hg.
Let x be the amount of N2O5 decomposed after 30 min.
∴ After 30 min.
Pressure due to N2O5 = 233.8 – x ; Pressure due to NO2 = 2x
and pressure due to O2 = x/2
Total pressure after 30 min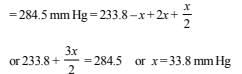
Hence pressure of N2O5 after 30 min.
= 233.8 – 33.8 = 200 mm Hg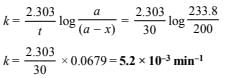
10. Two reactions (i) A → products, (ii) B → products, follows first order kinetics. The rate of the reaction : (i) is doubled when the temperature is raised from 300K to 310K. The half life for this reaction at 310K is 30 minutes. At the same temperature B decomposes twice as fast as A. If the energy of activation for the reaction, (ii) is half that of reaction (i), calculate the rate constant of the reaction (ii) at 300K. (1992 - 3 Marks)
Solution:


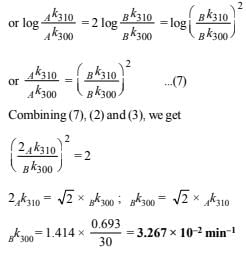
|
446 docs|929 tests
|
















