JEE Advanced (Subjective Type Questions): Electromagnetic Induction & Alternating Current- 2 | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.11. A solenoid has an inductance of 10 henry and a resistance of 2 ohm. It is connected to a 10 volt battery. How long will it take for the magnetic energy to reach 1/4 of its maximum value? (1996 - 3 Marks)
Ans. 3.466 sec
Solution. KEY CONCEPT : Let I0 be the current at steady state. The magnetic energy stored in the inductor at this state will be
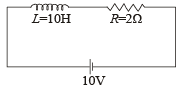

This is the maximum energy stored in the inductor. The current in the circuit for one fourth of this energy can be found as
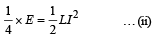
Dividing equation (i) and (ii)
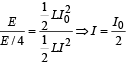
Also, V = I0 R
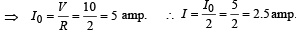
The equation for growth of current in L-R circuit is
I = I0 [1 – e – Rt/L]
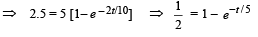
⇒ t = 5 loge 2 = 2 × 2.303 × 0.3010 = 3.466 sec.
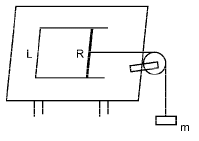
Q.12. A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m, tied to the other end of the string hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate. (1997 - 5 Marks)
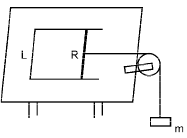
Ans.
Solution. KEY CONCEPT : If v is the velocity of the rod at any time t, induced emf is BvL and so induced current in the rod
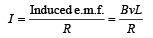
Due to this current, the rod in the field B will experience a force

So, equation of motion of the rod will be,
T – F = 0 × a, i.e., T = F [as rod is massless]
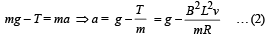
So rod will acquire terminal velocity when its acceleration is zero i.e.,
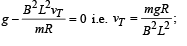
For the case when velocity is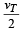
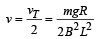
Substituting this value of velocity in eq. (2) we get
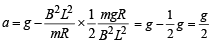
Q.13. A magnetic field 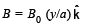 is into the paper in the +z direction. B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R, in x – y plane, starts falling under the influence of gravity see figure) Note the directions of x and y axes in figure. (1999 - 10 Marks)
is into the paper in the +z direction. B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R, in x – y plane, starts falling under the influence of gravity see figure) Note the directions of x and y axes in figure. (1999 - 10 Marks)
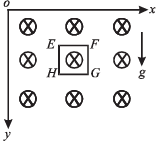
Find
(a) the induced current in the loop and indicate its direction.
(b) the total Lorentz force acting on the loop and indicate its direction, and
(c) an expression for the speed of the loop, v(t) and its terminal value.
Ans.
Solution. Suppose at t = 0, y = 0 and t = t, y = y (a)
Total magnetic flux 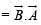
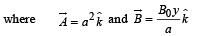
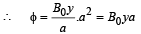
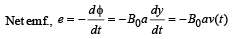
As total resistance = R
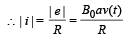
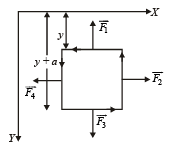
NOTE : Now as loop goes down, magnetic flux linked with it increases, hence induced current flows in such a direction so as to reduce the magnetic flux linked with it. Hence, induced current flows in anticlockwise direction.
(b) Each side of the cube will experience a force as shown (since a current carrying segment in a magnetic field experiences a force).
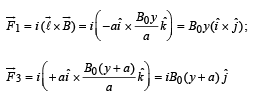
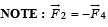 and hence will cancel out each other..
and hence will cancel out each other..
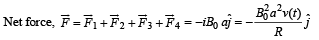
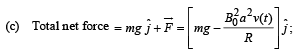
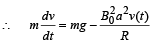
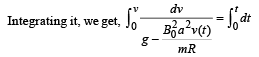
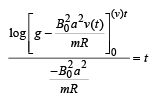
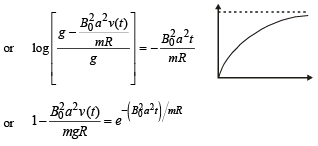
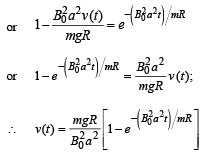
When terminal velocity is attained, v (t) does not depend on t
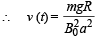
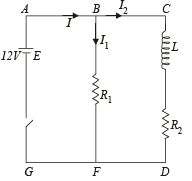
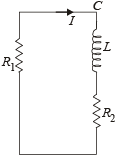
Q.14. An inductor of inductance L = 400 mH and resistors of resistances R1 = 2Ω and R2 = 2 Ω are connected to a battery of emf E = 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t = 0. What is the potential drop across L as a function of time? After the steady state is reached, the switch is opened. What is the direction and the magnitude of current through R1 as a function of time? (2001-5 Marks)
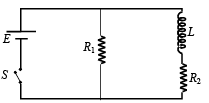
Ans. 12e–5tV, 3e–10tA, clockwise
Solution. This is a question on growth and rise of current.
GROWTH OF CURRENT : Let at any instant of time t the current be as shown in the figure.
Applying Kirchoff’s law in the loop ABCDFGA we get, starting from G moving clockwise
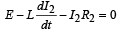
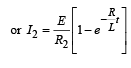
Also we know that the emf (V) produced across the inductor
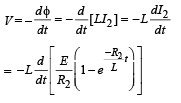
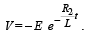 Here the negative sign shows the opposition to the growth of current.
Here the negative sign shows the opposition to the growth of current.
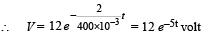
DECAY OF CURRENT : When the switch is opened, the branch AG is out of the circuit. Therefore, the current decays through the circuit CBFDC (in clockwise direction).
Applying Kirchhoff 's law
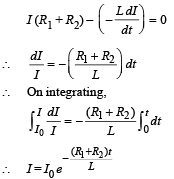
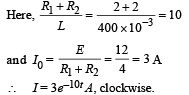
Alternatively, you may directly find the time constant 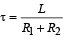 and use the equation i = i0e - t/τ where i0 = 6A
and use the equation i = i0e - t/τ where i0 = 6A
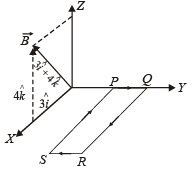
Q.15. A rectan gular loop PQRS made fr om a uniform wire has length a, width b and mass m. It is free to rotate about the arm PQ, which remains hinged along a horizontal line taken as the y-axis (see figure). Take the vertically upward direction as the z-axis. A uniform magnetic field 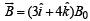 exists in the region. The loop is held in the x-y plane and a current I is passed through it. The loop is now released and is found to stay in the horizontal position in equilibrium. (2002 - 5 Marks)
exists in the region. The loop is held in the x-y plane and a current I is passed through it. The loop is now released and is found to stay in the horizontal position in equilibrium. (2002 - 5 Marks)
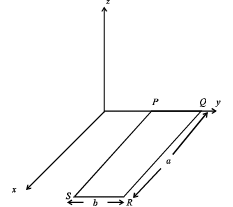
(a) What is the direction of the current I in PQ?
(b) Find the magnetic force on the arm RS.
(c) Find the expression for I in terms of B0, a, b and m.
Ans. (a) P to Q
Solution. Let us consider the current in the clockwise direction in loop PQRS. Force on wire QR,
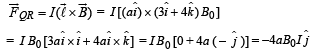
Force on wire PS
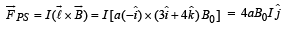
Thus we see that force on QR is equal and opposite to that on PS and balance each other.
The force on RS is
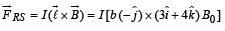
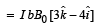 ... (i)
... (i)
The torque about PQ by this force is
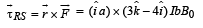
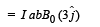 .. (ii)
.. (ii)
The torque about PQ due to weight of the wire PQRS is
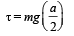 ... (iii)
... (iii)
For the wire loop to be horizontal, we have to equate (ii) and
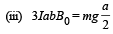
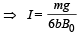 ... (iv)
... (iv)
Therefore, (a) Th e direction of current assumed is right . This is because torque due to mg and current are in opposite directions. Therefore, current is from P to Q.
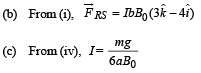
Q.16. A metal bar AB can slide on two parallel thick metallic rails separated by a distance ℓ. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t = 0, it is made to slide on the rails away from the wire. Answer the followin g questions. (2002 - 5 Marks)
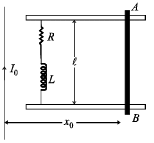
(a) Fin d a relation amon 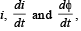 where i is the current in the circuit and f is the flux of the magnetic field due to the long wire through the circuit.
where i is the current in the circuit and f is the flux of the magnetic field due to the long wire through the circuit.
(b) It is observed that at time t = T, the metal bar AB is at a distance of 2x0 from the long wire and the resistance R carries a current i1. Obtain an expression for the net charge that has flown through resistance R from t = 0 to t = T.
(c) The bar is suddenly stopped at time T. The current through resistance R is found to be 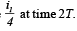 Find the value of L/R in terms of the other given quantities.
Find the value of L/R in terms of the other given quantities.
Ans.
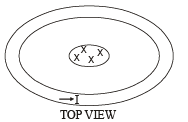
Solution. (a) KEY CONCEPT : As the metal bar AB moves towards the right, the magnetic flux in the loop ABCD increases in the downward direction. By Lenz's law, to oppose this, current will flow in anticlockwise direction as shown in figure.
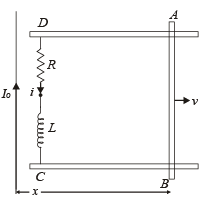
Applying Kirchhoff 's loop law in ABCD, we get
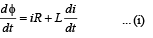
(b) Let AB be at a distance x from the long straight wire at any instant of time t during its motion. The magnetic field at that instant at AB due to long straight current carrying wire is
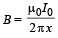
The change in flux through ABCD in time dt is
dφ = B (dA) = Bℓdx
Therefore, the total flux change when metal bar moves from a distance x0 to 2x0 is
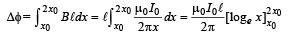
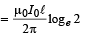 ... (ii)
... (ii)
The charge flowing through resistance R in time T is
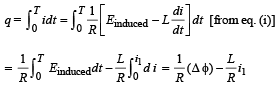
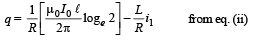
(c) When the metal bar AB is stopped, the rate of change of magnetic flux through ABCD becomes zero.
From (i),
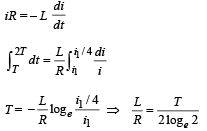
Q.17. A square loop of side ‘a’ with a capacitor of capacitance C is located between two current carrying long parallel wires as shown. The value of I in the wires is given as I = I0 sinωt. (2003 - 4 Marks)
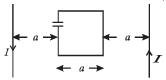
(a) Calculate maximum current in the square loop.
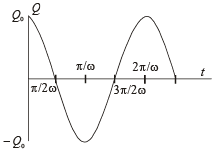
(b) Draw a graph between charges on the upper plate of the capacitor vs time.
Ans.
Solution. (a) Let us consider a small strip of thickness dx as shown in the figure.
The magnetic field at this strip
B = BA + BB
(Perpendicular to the plane of paper directed upwards)
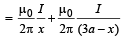
BA = Magnetic field due to current in wire A
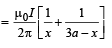
BB = Magnetic field due to current in wire B
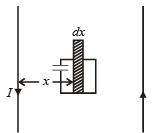
Small amount of magnetic flux passing through the strip of thickness dx is
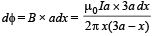
Total flux through the square loop
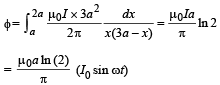
The emf produced
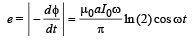
Charge stored in the capacitor
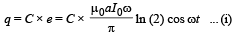
∴ Current in the loop
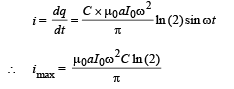
(b) From (i), the graph between charge and time is
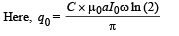
Q.18. In a series L–R circuit (L = 35 mH and R = 11 Ω), a variable emf source (V = V0 sin ωt) of Vrms = 220 V and frequency 50 Hz is applied. Find the current amplitude in the circuit and phase of current with respect to voltage. Draw current-time graph on given graph (π = 22/7). (2004 - 4 Marks)
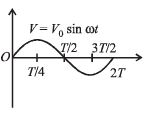
Ans.
Solution.
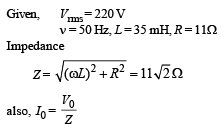
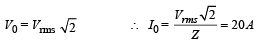
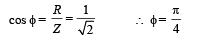
∴ graph is given by.
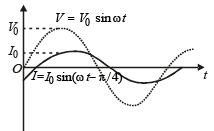
Q.19. In the figure both cells A and B are of equal emf. Find R for which potential difference across battery A will be zero, long time after the switch is closed. Internal resistance of batteries A and B are r1 and r2 respectively (r1 > r2). (2004 - 4 Marks)
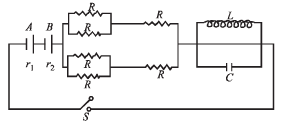
Ans.
Solution. NOTE : After a long time capacitor will be fully charged, hence no current will flow through capacitor and all the current will flow from inductor. Since current is D.C., resistance of L is zero.
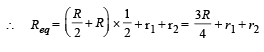
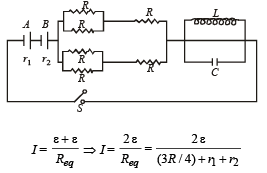
Potential drop across A is
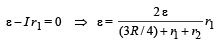
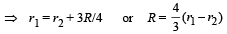
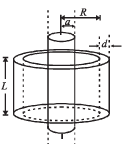
Q.20. A long solenoid of radius a and number of turns per unit length n is enclosed by cylindrical shell of radius R. thickness d (d << R ) and length L. A variable current i = i0 sinwt flows through the coil. If the resistivity of the material of cylindrical shell is ρ, find the induced current in the shell. (2005 - 4 Marks)
Ans.
Solution. KEY CONCEPT : The magnetic field in the solenoid is given by
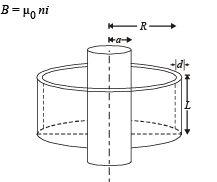
⇒ B = µ0 ni0 sin ωt [∵ i = i0 = sin ωt (given)]
The magnetic flux linked with the solenoid
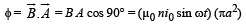
∴ The rate of change of magnetic flux through the solenoid
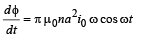
The same rate of change of flux is linked with the cylindrical shell. By the principle of electromagnetic induction, the induced emf produced in the cylindrical shell is
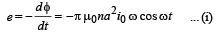
The resistance offered by the cylindrical shell to the flow of induced current I will be
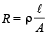
Here, ℓ = 2π R and A = L × d
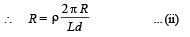
The induced current I will be
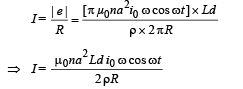
|
481 docs|964 tests
|
















